ABC218 A～E問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC218(AtCoder Beginner Contest 218)　A～E問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Weather Forecast

N文字目が○ならばYes、xならばNoを出力します。
if文で分岐して出力すればよいです。

以下の点に注意してください。
・pythonの文字列は最初が「0文字目」
　たとえば「oxxxoox」を受け取った時、「0文字目」=S[0]はo、「1文字目」=S[1]はx、...になります。
　よって問題文で言うN文字目はpythonでは「N-1文字目」=S[N-1]となります。

・文字列は""で囲う
　以下のように書くとエラーになります。

【間違い】

if S[N-1]==o:
    print(Yes)
else:
    print(No)

○、Yes、Noはそれぞれ文字列であるため、"○"、"Yes"、"No"としましょう。

【正解】

if S[N-1]=="o":
    print("Yes")
else:
    print("No")

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
# Nは数字
N=int(input())
# Sは文字列
S=input()

# SのN文字目(S[N-1])が"o"なら
if S[N-1]=="o":
    # Yesを出力
    print("Yes")
# そうでないならば(SのN文字目(S[N-1])が"x"なら)
else:
    # Noを出力
    print("No")

B - qwerty

1→A
2→B
...
と変換するような関数を作っても解けますが26個条件分岐を書くのは面倒くさいです。

コンピュータで扱う文字には文字コードという番号がついており、pythonでは
文字コード→文字
への変換ができるchrという関数があります。

chr(文字コード番号)=文字

例えば『a』の文字コードは97なので
chr(97)="a"
となります。

a,b,c,...の文字コードは97,98.99,...と連番になっているため、chr(Pの値+96)とすれば欲しい文字へ変換ができます。

【提出】

# 入力の受け取り
P=list(map(int, input().split()))

# 答えを格納する変数
ans=""

# P1~P26(P[0]~P[25])まで
for x in P:
    # 文字コードx+96の文字をansの末尾へ追加
    ans+=chr(x+96)

# 答えを出力
print(ans)

C - Shapes

C問題にしては高難易度の問題でした。
コンテスト参加中にC問題がなかなか解けないとなったらかなり焦りますが、諦めてさっさとD、E問題へ進みましょう。
実際今回のコンテストはC問題よりもD、E問題を解けた人が多く、Cを早めに諦めた人のほうがパフォーマンスが高くなりました。

まずこういったグリッドを与えられる問題を初めて見た人は入力の受け取りに戸惑うと思います。
以下の手順で受け取りましょう。
(1)空のリストを用意(S)
(2)一行ずつ文字列で受け取り(S_tmp)
(3)文字列をリストへ変換(1文字ずつのリストになります)
(4)変換したリストをSへ追加

# N行受け取り
for i in range(N):
    # 文字列でSを受け取り
    S_tmp=input()
    # リストに変換
    S_tmp=list(S_tmp)
    # Sへ格納
    S.append(S_tmp)

こうしてやるとS[行番号][列番号]としてそれぞれのマスが「.」か「#」か確認できます。

解法は以下の手順です。

(1)シャープの個数を数える
S、Tのシャープの個数を数えましょう。個数が違っていたらなにをしようが一致しないので「No」を出力して終了です。

(2)回転する
次に回転ですがこれは4通り(90度、180度、270度、360(0)度)しかないのですべて試してみればOKです。
回転する、というのがどういう座標の変換になるのか考えましょう。

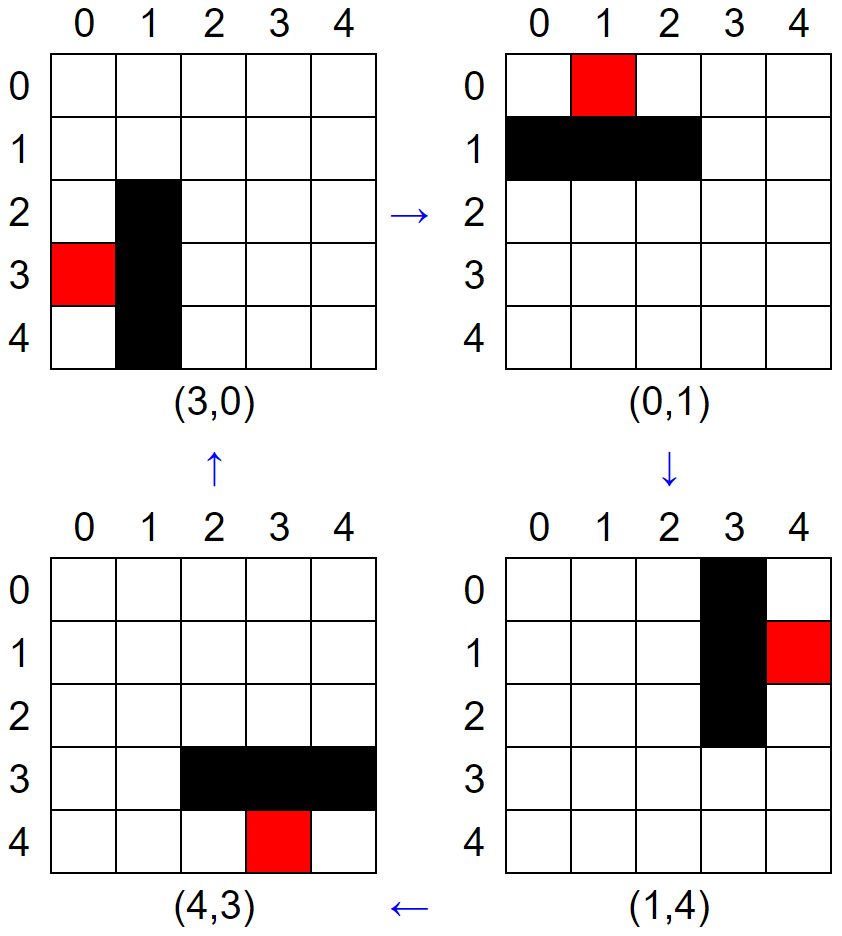
図の赤色の部分に注目しましょう。
(行番号,列番号)として
(3,0)
(0,1)
(1,4)
(4,3)
と変化していきます。
「回転前の列番号」が「回転後の行番号」になるのはなんとなくわかりますね。
「回転後の列番号」は少し分かりづらいですが「4-回転前の行番号」になっています。
この4というのは0始まりにしたときの行、列の大きさ、つまりN-1です。

まとめると90度時計回りに回転するというのは
(行番号,列番号)→(列番号,(N-1)-行番号)
と変換する、ということになります。

(3)平行移動する
回転していい感じに図のようになったとします。

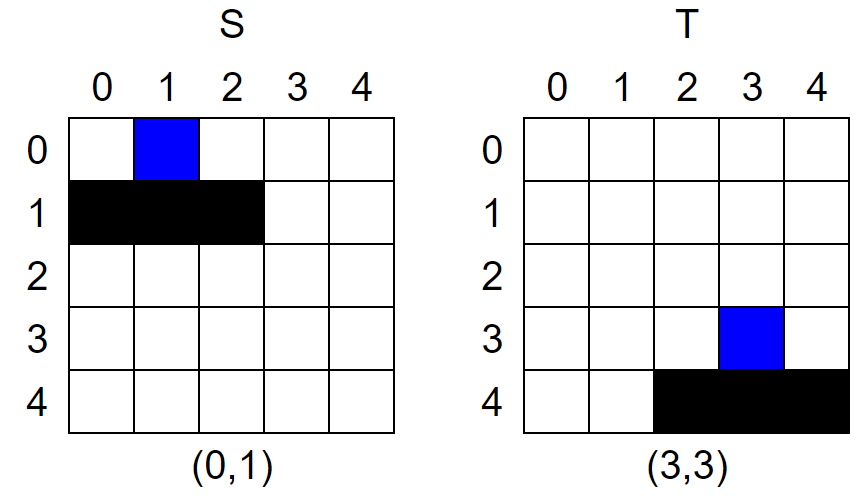
まず左上からマスを見ていき、初めて#がでてきた座標を確認します。図の青い部分です。
もし図形の形が一致しているなら、ここを合わせるように平行移動すれば完全一致するはずです。
ですので(0,1)→(3,3)となるように平行移動するわけですがこれは簡単で
行：下方向に3(3-0)→行+3
列：右方向に2(3-1)→列+2
となります

まとめると平行移動は
左上からはじめてシャープの出る行、列番号の差を確認し、
(行番号,列番号)→(行番号+下方向への移動量,列番号+右方向への移動量)
と変換する、ということになります。

実装の際はそれぞれを行う関数を用意すると楽です。
すなわち以下5つを作ります。
・#の個数を確認する関数：count_sharp(X)
・90度時計回りに回転する関数：rotate(X)
・左上から探索して初めて#が出てくる行番号,列番号を返す関数：first_sharp(X)
・下方向へmove_gyou,右方向へmove_retu平行移動する関数：Translation(X,move_gyou,move_retu)
・S,Tが一致しているか確認する関数：check(S,T)

【提出】

# #の個数を確認する関数
def count_sharp(X):
    # #の個数をカウントする変数
    count=0
    # 行0～Nまで
    for gyou in range(N):
        # 列0～Nまで
        for retu in range(N):
            # もしx[行番号][列番号]が#なら
            if X[gyou][retu]=="#":
                # カウントにプラス1
                count+=1
    # カウント数を返す
    return count

# 90度時計回りに回転する関数
def rotate(X):
    # 回転後のグリッド
    rotate_X=[["."]*N for i in range(N)]
    # 行0～Nまで
    for gyou in range(N):
        # 列0～Nまで
        for retu in range(N):
            # (行番号,列番号)→(列番号,(N-1)-行番号)
            rotate_X[retu][N-1-gyou]=X[gyou][retu]
    # 回転後のグリッドを返す
    return rotate_X

# 左上から探索して初めて#が出てくる行番号,列番号を返す関数
def first_sharp(X):
    # 行0～Nまで
    for gyou in range(N):
        # 列0～Nまで
        for retu in range(N):
            # もしx[行番号][列番号]が#なら
            if X[gyou][retu]=="#":
                # 行番号,列番号を返して終了
                return gyou,retu

# 下方向へmove_gyou,右方向へmove_retu平行移動する関数
def Translation(X,move_gyou,move_retu):
    # 平行移動後のグリッド
    move_X=[["."]*N for i in range(N)]
    # 行0～Nまで
    for gyou in range(N):
        # 列0～Nまで
        for retu in range(N):
            # 行番号+move_gyou,列番号+move_retuがグリッドの中にあれば
            if 0<=gyou+move_gyou<N and 0<=retu+move_retu<N:
                # (行番号,列番号)→(行番号+move_gyou,列番号+move_retu)
                move_X[gyou+move_gyou][retu+move_retu]=X[gyou][retu]
    # 平行移動後のグリッドを返す
    return move_X

# S,Tが一致しているか確認する関数
def check(S,T):
    # 行0～Nまで
    for gyou in range(N):
        # 列0～Nまで
        for retu in range(N):
            # もしS[gyou][retu]とT[gyou][retu]が一致しなければ
            if S[gyou][retu]!=T[gyou][retu]:
                # Falseを返して終了
                return False
    # 完全に一致していればTrueを返す
    return True

# 入力の受け取り
N=int(input())
# S,Tを用意
S=[]
T=[]

# N行受け取り
for i in range(N):
    # 文字列でSを受け取り
    S_tmp=input()
    # リストに変換
    S_tmp=list(S_tmp)
    # Sへ格納
    S.append(S_tmp)

# N行受け取り
for i in range(N):
    # 文字列でTを受け取り
    T_tmp=input()
    # リストに変換
    T_tmp=list(T_tmp)
    # Tへ格納
    T.append(T_tmp)

# #の数が違う場合
if count_sharp(S)!=count_sharp(T):
    # Noを出力
    print("No")
    # 終了
    exit()

# 4回回転する(90→180→270→360(0))
for i in range(4):
    # Sを回転
    S=rotate(S)
    # S,Tの最初の#が出てくる行番号、列番号を確認
    S_first_gyou,S_first_retu=first_sharp(S)
    T_first_gyou,T_first_retu=first_sharp(T)

    # 行平行移動量=Tの最初の#が出てくる行番号-Sの最初の#が出てくる行番号
    move_gyou=T_first_gyou-S_first_gyou
    # 列平行移動量=Tの最初の#が出てくる列番号-Sの最初の#が出てくる列番号
    move_retu=T_first_retu-S_first_retu

    # Sを下方向へmove_gyou,右方向へmove_retu平行移動
    S_Trans=Translation(S,move_gyou,move_retu)

    # 一致しているかチェック
    if check(S_Trans,T)==True:
        # 一致していたらYesを出力
        print("Yes")
        # 終了
        exit()

# 4回転試して一致しなければNoを出力
print("No")

D - Rectangles

制約が4≤N≤2000なのでO(N^2)の解法でもTLEはなさそうです。

長方形というのは対角線上の点が決まれば他の点の場所が決まります。

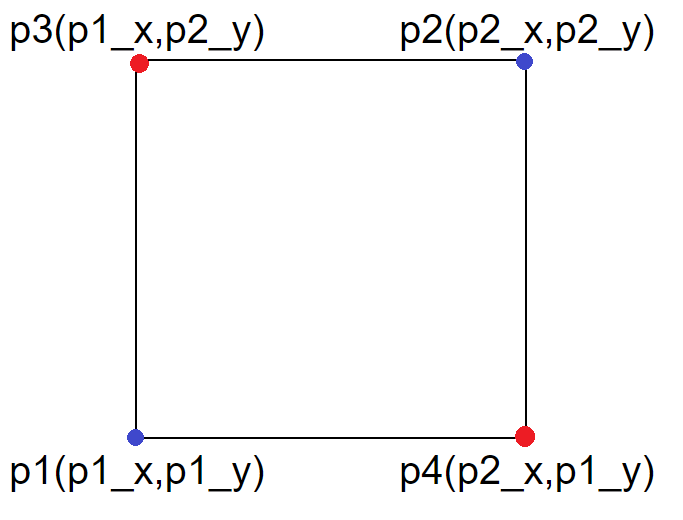
例えば図の青い点p1,p2がきまればp3,p4の座標は定まります。
具体的には
p1(p1_x,p1_y)
p2(p2_x,p2_y)
ならば
p3(p1_x,p2_y)
p4(p2_x,p1_y)
となります。

このp3,p4に当たる点が存在するかをチェックすればOKです。

が、リストの中からp3,p4があるかチェックしていれば終わりません。
そこでdefaultdictを使いましょう。
使ったことがない人は以下を読んでください。

defaultdict(連想配列)について
辞書または連想配列と言います。
キー：値
というような対応付を行えるデータ構造です。(辞書という言い方もします)
連想配列はdict()と書くことでも使えますがデフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import：from collections import defaultdict
作成(デフォルト0)：変数名=defaultdict(int)
キー、値の登録：変数名[キー]=値
値の取り出し：変数名[キー]
【使用例】

# インポート
from collections import defaultdict

# 作成(デフォルト0)：変数名=defaultdict(int)
dictionary=defaultdict(int)

# キー、値の登録：変数名[キー]=値
dictionary[5]=1

# 値の取り出し：変数名[キー]
x=dictionary[5]

詳しく知りたい人は以下を参照してください。

defaultdictはキーの部分にタプルを使用できます。
タプルはリストのようなもので、たとえば(1,3)をキーとした値を1、というような登録ができます。

具体的にはまずp_existというdictを用意します。
そしてx,yの受け取りと同時にp_exist[(x,y)]=1としておきます。
こうすることで座標が(x,y)の点が存在するかどうか⇔p_exist[(x,y)]=1か　で確認できるというわけです。

あとは二重ループですべての点の組を確認します。点の組を(p1,p2)としたときにp3,p4にあたる点があるかどうか確認すればOKです。
※p1,p2のx座標またはy座標が一致している場合は長方形を作りようがないのでスルーします。
ただしそれぞれの長方形について対角線の点のとり方は「左下」と「右上」、「左上」と「右下」の二通り存在するので二重にカウントしてしまいます。
そのため答えの出力前に割る2しておきましょう。

【提出】

# 入力を受け取り
N=int(input())

# 座標の格納用リスト
points=[]

# defaultdictを用意
from collections import defaultdict
p_exist=defaultdict(int)

# M行受け取り
for i in range(N):
    # x,yを受け取り
    x,y=map(int, input().split())
    # 座標をpointsへ格納
    points.append([x,y])
    # dictに1を記録
    p_exist[(x,y)]=1

# 答えを格納する変数
ans=0

# p1=0~Nまで
for p1 in range(N):
    # p2=p1+1~Nまで
    for p2 in range(p1+1,N):
        # p1のx座標,y座標
        p1_x,p1_y=points[p1]
        # p1のx座標,y座標
        p2_x,p2_y=points[p2]

        # x座標またはy座標が同じ場合は
        if p1_x==p2_x or p1_y==p2_y:
            # 次の点へ
            continue
        # 座標(p1_x,p2_y)と座標(p2_x,p1_y)の点がそんざいすれば
        if p_exist[(p1_x,p2_y)]==1 and p_exist[(p2_x,p1_y)]==1:
            # 答えにプラス1
            ans+=1

# 二重に数えているので2で割る
ans//=2
# 答えを出力
print(ans)

E - Destruction

UnionFindというデータ構造を使います。

cが0以下の辺は取り除く意味がないということはすぐにわかります。
どの辺を取り除いてよいか？を考えると難しいので最初に辺を全て取っ払い、必要なものだけ安い順につなげましょう。

以下の手順で解きます。
(1)すべての辺を取り除き、報酬をすべて受け取ります(報酬がプラスのもののみ受け取ります)
(2)報酬が低い順に辺を並び替えます
(3)報酬が0以下の辺を全てつなぎます
(4)報酬が0より大きい辺について
　・A,Bが連結なら無視します
　・A,Bが非連結なら報酬Cを返して(受け取った報酬からマイナスCして)辺をつなぎます

(4)のA,Bが連結かどうか？の判定とA,Bの連結にUnionFindを使います。

UnionFindはグループ分けを高速でできるデータ構造です。
具体的には以下のことができます。
・a,bを同じグループとする⇔a,bを連結する：O(logN)くらい(厳密には違いますがO(logN)くらいと思っておけばOKです)
・a,bが同じグループか判定する⇔a,bが連結か確認する：O(1)くらい(厳密には状況により違いますがO(1)くらいと思っておけばOKです)
とにかくめちゃくちゃ速く上記2つができるデータ構造だと思えば良いです。

きちんとした説明はAtCoder公式が解説スライドを作っているのでそちらを御覧ください。

実装はかなり難しいです。ですが問題を解くのにそこまで理解する必要はなく、以下のUnionFindクラスをコピペして使えればOKです。

# UnionFindを用意
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n
 
    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]
 
    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 
 
    def same(self,a,b):
        return self.leader(a) == self.leader(b)
 
    def size(self,a):
        return abs(self.parent_size[self.leader(a)])
 
    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

上記をコードの最初にコピペしてから以下のように使います。
・初期化：変数名=UnionFind(要素の数)
・根の確認：変数名.leader(要素番号)
・グループ化：変数名.merge(要素番号1,要素番号2)
・同一グループかの確認：変数名.same(要素番号1,要素番号2)
　(同一ならTrue,違うグループならFalseを返す)
・所属するグループのサイズ確認：変数名.size(要素番号)
・グループ全体の確認：変数名.groups()

【初期化時の注意事項】
本問のように頂点の番号が1から始まる場合、
初期化：変数名=UnionFind(N+1)
としなければならないことに注意してください。
このクラスは頂点番号が0インデックスでの使用を想定しているためです。

【使用例】

# 初期化：変数名=UnionFind(要素の数)
UniFi=UnionFind(10)

# グループ化：変数名.merge(要素番号1,要素番号2)
UniFi.merge(0,2)
UniFi.merge(1,3)
UniFi.merge(3,0)

# 根の確認：変数名.leader(要素番号)
leader_x=UniFi.leader(1)

# 同一グループかの確認：変数名.same(要素番号1,要素番号2)
if UniFi.same(1,5)==True:
    print("同一グループ")
else:
    print("別グループ")

# 所属するグループのサイズ確認：変数名.size(要素番号)
size_x=UniFi.size(1)

# グループ全体の確認：変数名.groups()
print(UniFi.groups())

UnionFindのより詳細な説明、クラスの内容の解説については拙著『AtCoder　凡人が『緑』になるための精選50問詳細解説』に記載しています。
内容までしっかり理解しておきたいという人は購入をご検討ください。
詳細は本ページ下部【広告】を御覧ください。

この問題では
・a,bが連結かどうか？→same(a,b)がTrueか？
・a,bの連結→merge(a,b)
とUnionFindを使うことで確認と連結を高速で行うことができ、TLEせずに解けます。

【提出】

# UnionFindを用意
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n
 
    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]
 
    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 
 
    def same(self,a,b):
        return self.leader(a) == self.leader(b)
 
    def size(self,a):
        return abs(self.parent_size[self.leader(a)])
 
    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

# 入力の受け取り
N,M=map(int, input().split())

# 辺の情報格納用リスト
edge=[]

# 答えの格納用変数
ans=0

# M行受け取り
for i in range(M):
    A,B,C=map(int, input().split())
    # 後のソートのためC先頭で格納
    edge.append([C,A,B])
    # Cがプラスなら
    if 0<C:
        # 答えにCをプラス
        ans+=C

# 辺の報酬が低い順にソート
edge.sort()

# UnionFindを初期化(頂点数N+1個(0~N))
UniFi=UnionFind(N+1)

# edgeの各要素について
for c,a,b in edge:
    # もしcが0以下なら
    if c<=0:
        # つなぐ
        UniFi.merge(a,b)
    # そうでないならば(cが0より大きいなら)
    else:
        # もしa,bがまだつながっていない=連結でないならば
        if UniFi.same(a,b)==False:
            # cの報酬を返す
            ans-=c
            # a,bをつなぐ
            UniFi.merge(a,b)

# 答えを出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】