14 数学問題1 Dif:274 ABC181 C：「AtCoder 凡人が『緑』になるための精選50問詳細解説」サンプル

この記事は拙著「AtCoder　凡人が『緑』になるための精選50問詳細解説」のサンプルです
価格：100円
kindle：https://www.amazon.co.jp/dp/B09C3TPQYV
booth(pdf)：https://sano192.booth.pm/items/3179185

前：https://qiita.com/sano192/items/fee4234d2942ea6c02a5
次：https://qiita.com/sano192/items/b9967d40093c4c3be42d

【目標】
・「二次元平面上で3点が同一直線上にあるか判定する方法」を覚える
・知らない知識を要求された場合の対処法を身につける

【概要】
この問題のように高校数学程度の知識が要求される問題はC~D問題あたりで時々出題される。しかし時々出題される数学問題のためにわざわざ1から数学の勉強し直しをするなんてめちゃくちゃ面倒くさい。コンテスト中にgoogleを駆使して数学問題に喰らいつく方法を身につけよう。

【方針】
この問題を解くには「二次元平面上で3点が同一直線上にあるか判定する方法」を知っていなければならない。
知らなかったらどうするか。さっさとgoogleを開こう。

「3点　同一直線上」で検索し、上から5つくらいを開いて中身を確認する。内容を全て読む必要はない。欲しい情報があるかどうかをざっと見て確認していく。特に具体例があるページは役に立つことが多い。

ではここから「二次元平面上で3点が同一直線上にあるか判定する方法」を説明する。
まず2点(x1,y1),(x2,y2)を通る直線の方程式を思い出そう。これも忘れていれば検索だ。
以下が「2点(x1,y1),(x2,y2)を通る直線の方程式」

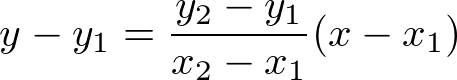
変形して

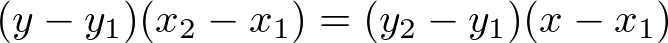
これが2点を通る直線だ。
3点目がこの直線の上にある=3点目(x3,y3)を代入してイコールが成り立つということ。
つまり以下の条件を満たせば(x1,y1),(x2,y2),(x3,y3)は同一直線状にあるといえる。

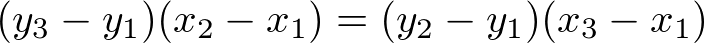
検索して出てきたページも多少書き方は違えど最終的な結論としては同じ式が出てきているはずだ。

※厳密に言うとx1=x2の場合、最初の方程式で0除算が発生するのでこの式変形は正しくない。しかし最後の式は「二次元平面上で3点が同一直線上にあるか判定する」ためには正しい式となっている。

これで判定方法はわかった。
あとは3点の組み合わせ全てについて判定すれば良さそうだが、TLE(実行時間制限超過)しないか計算量を確認しておこう。

制約は3<=N<=10^2。つまりで3点の組み合わせは最大でN^3=10^6個以下となり、これならなんとか間に合いそうだ。
どうやって3点の組み合わせを全て確認するか？については【実装】で解説する。

【実装】
まず入力を受け取る。座標はpointsという二次元配列に格納する。

N=int(input())

points=[]
for i in range(N):
    x,y=map(int, input().split())
    points.append([x,y])

3つの点の組み合わせをもれなく探索する方法について考えよう。
たとえば5種類の点(0番目の点~4番目の点)がある場合、以下のように組み合わせが列挙できればいい。
0 1 2
0 1 3
0 1 4
0 2 3
0 2 4
0 3 4
1 2 3
1 2 4
1 3 4
2 3 4
上記10個が3つの組み合わせの全てだ。
1番上の
0 1 2
は
0番目の点と、1番目の点と、2番目の点
の組み合わせであることを表す。

この組をどのように作るか。以下のように3重ループを組むとうまくいく。

for i in range(N):
    for j in range(i+1,N):
        for k in range(j+1,N):

1回目のループは
i=0
j=1(jはi+1から始まる)
k=2(kはj+1から始まる)
で
0 1 2
が作れる。

2回目のループは一番内側のkだけ増えるので
i=0
j=1
k=3
で
0 1 3
が作れる。

3回目は
i=0
j=1
k=4
で
0 1 4
が作れる。

ここでkのループが終わり、今度はjが+1される。

4回目は
i=0
j=2
k=3
で
0 2 3
が作れる。

ではループが進み、i=3となったらどうなるか。
i=3
j=4
となるがN=5(5種類の点)であるため

        for k in range(j+1,N):

この部分でrange(5, 5)となり、kに何も入らず、何も処理されない。

つまり余分な部分は何も処理されずにループが回ってくれるので、結果として3数の組み合わせを列挙できる。

よくわからなければ以下のコードをコピペしてステップ実行してみよう。

N=5
for i in range(N):
    for j in range(i+1,N):
        for k in range(j+1,N):
            print(i,j,k)

i、j、kがうまく増えていくのがわかると思う。
組み合わせを列挙する際、この書き方は非常によく使うのでしっかり理解して次に進んでほしい。

上記を使って3点の組み合わせを作り、条件が成り立つかを確かめよう。
まず変数x1,y1,x2,y2,x3,y3に3点のx座標、y座標を代入する。

for i in range(N):
    for j in range(i+1,N):
        for k in range(j+1,N):
            x1,y1=point[i][0],point[i][1]
            x2,y2=point[j][0],point[j][1]
            x3,y3=point[k][0],point[k][1]

3点の組み合わせ全てについて条件が成り立てば「Yes」を出力して終了。
条件が成り立たなければ=ループがすべて終われば「No」を出力する。

            if (x2-x1)*(y3-y1)==(y2-y1)*(x3-x1):
                print("Yes")
                exit()

print("No")

【コード全文】

N=int(input())

points=[]
for i in range(N):
    x,y=map(int, input().split())
    points.append([x,y])

for i in range(N):
    for j in range(i+1,N):
        for k in range(j+1,N):
            x1,y1=points[i][0],points[i][1]
            x2,y2=points[j][0],points[j][1]
            x3,y3=points[k][0],points[k][1]
 
            if (x2-x1)*(y3-y1)==(y2-y1)*(x3-x1):
                print("Yes")
                exit()

print("No")

この記事は拙著「AtCoder　凡人が『緑』になるための精選50問詳細解説」のサンプルです
価格：100円
kindle：https://www.amazon.co.jp/dp/B09C3TPQYV
booth(pdf)：https://sano192.booth.pm/items/3179185

前：https://qiita.com/sano192/items/fee4234d2942ea6c02a5
次：https://qiita.com/sano192/items/b9967d40093c4c3be42d