モノグサプログラミングコンテスト2022(ABC238) A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

モノグサプログラミングコンテスト2022(AtCoder Beginner Contest 238)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

モノグサ株式会社様について

本コンテストはモノグサ株式会社様が主催されています。
興味のある方は採用ページを御覧ください。

採用ページはかなり気合の入った作りをしていて、ポジションごとに詳細を記載しています。
転職する気がなくても眺めてみるのは面白いかもしれません。

A - Exponential or Quadratic

2^nとn^2を計算して比較すれば終わりです・・・としたいところですが制約に「nは1以上10^9以下の整数」とあります。
最悪の場合でnが10^9なら
2^(1000000000)
を計算する羽目になります。コンピューターといえどこんな大きな数の計算はすぐにはできません。

n=1,2,3,...について2^nとn^2がどのようになるか計算してみましょう。

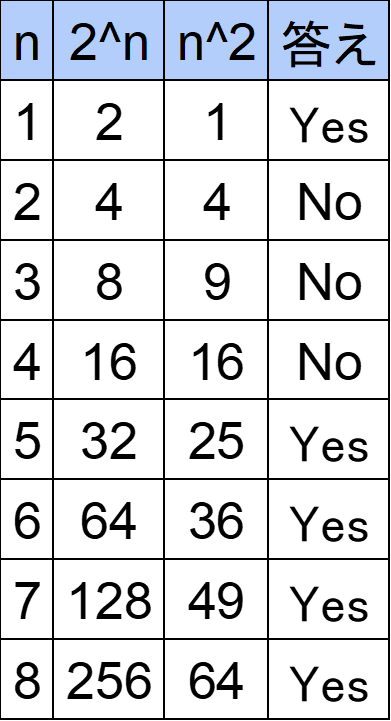
nが1の場合は特殊として、nが4までは「No」、5以上なら「Yes」になることがわかります。
厳密にやるなら数学的帰納法なり微分なりしなければならないですが、「2^nのほうがすぐバカでかくなるじゃん」ということがわかれば十分です。

よって以下のように条件分岐します。
・nが2,3,4　→　「No」を出力
・上記以外　→　「Yes」を出力

「Yes」「No」は文字列なので出力の際、"Yes","No"とダブルクオーテーションをつけてください。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
n=int(input())

# n=2またはn=3またはn=4
if n==2 or n==3 or n==4:
    # 「No」を出力
    print("No")
# そうでなければ
else:
    # 「Yes」を出力
    print("Yes")

B - Pizza

まず360度内にすることは考えず、何度の部分に切れ込みが入るか考えましょう。
A：90 180 45 195
であれば
0度
90度(0+90)
270度(90+180)
315度(270+45)
510度(315+195)

これを0～360度に直します。
510度=150度になりますが、これは510を360で割った余りと計算できます。
全部360で割った余りを取り、小さい順に並べましょう。
0 90 150 270 315
ついでに「360」を追加します。
0 90 150 270 315 360
それぞれの差がそれぞれのピザの中心角です。
すなわち
90-0=90
150-90=60
270-150=120
315-270=45
360-315=45

一番大きいのは120なので答えは120度となります。

余りを取るときは「%」
リストを小さい順に並び替えるときは
リスト.sort()
と書けばOKです。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))

# カットされた角度の格納 最初は0度
cut=[0]

# 角度
angle=0

# i=0~(N-1)
for i in range(N):
    # A[i]プラス
    angle+=A[i]
    # 角度を記録
    cut.append(angle)

# i=0~N
for i in range(N+1):
    # 360で割った余りを取る
    cut[i]%=360

# 小さい順に並び替え
cut.sort()

# 「360」を追加
cut.append(360)

# 答え
ans=0

# i=1~(N+1)
for i in range(1,N+2):
    # 現在までの「答え」と(cut[i]-cut[i-1])の差を比較
    # 大きい方を新しい答えとする
    ans=max(ans,cut[i]-cut[i-1])

# 答えを出力
print(ans)

C - digitnum

まずf(x)がどのような値を取るか、見てみましょう。
f(1)=1
f(2)=2
f(3)=3
...
f(9)=9
f(10)=1
f(11)=2
f(12)=3
f(13)=4
...
f(99)=90
f(100)=1
f(101)=2
...
f(999)=900
...

眺めているとf(1)~f(N)までの和は以下のようになっていそうです。
N=1~9：「1+2+...+N」
N=10~99：「1+2+...+9」+「1+2+...+(N-10+1)」
N=100~999：「1+2+...+9」+「1+2+...+90」+「1+2+...+(N-100+1)」
N=1000~9999：「1+2+...+9」+「1+2+...+90」+「1+2+...+900」「1+2+...+(N-1000+1)」
...

いい感じに書き直しましょう。
・10^0≤N<10^1：「1~(N-10^0+1)までの和」
・10^1≤N<10^2-1：「1～9までの和」+「1～(N-10^1+1)の和」
・10^2≤N<10^3-1：「1～9までの和」+「1～90の和」+「1～(N-10^2+1)の和」
・10^3≤N<10^4-1：「1～9までの和」+「1～90の和」+「1～900の和」+「1～(N-10^3+1)の和」
...

ここまでわかれば後は計算するだけです。

「A~Bまでの和」は「(B-A+1)*(A+B)/2」で計算できます。
関数として定義しておくと楽です。

【提出】

# 余りを定義
mod=998244353

# 入力の受け取り
N=int(input())

# A~Bまでの和
# 引数：A,B　→　返り値：A~Bまでの和
def S(A,B):
    return (B-A+1)*(A+B)//2

# 答え
ans=0

# x~1~18
for x in range(1,19):
    # 10^x≤Nならば
    if 10**x<=N:
        # 「1~9*10**(x-1)までの和」
        ans+=S(1,9*10**(x-1))
        # 余りを取る
        ans%=mod
    # 10^(x-1)≤N<10^xならば
    else:
        # 「1～(N-10^(x-1)+1)までの和」
        ans+=S(1,N-10**(x-1)+1)
        # 余りを取る
        ans%=mod
        # forを抜ける
        break

# 答えの出力
print(ans)

D - AND and SUM

1桁ずつx,yを決めていきます。
例えば2進数表記でa=「0001」、s=「1000」の場合を考えましょう。
実装と合わせて右端を「0桁目」、右端から一つ左に動いたところを「1桁目」、...と呼びます。

まずx AND y =aという条件からaが「1」の桁、すなわち0桁目はx,yともに必ず「1」でなければならないことがわかります。

その他の桁は「0」か「1」ですが、少なくとも一方は「0」でなければなりません。
とりあえずxのほうを全部「0」にしてしまいましょう。この後行うのはsの計算、すなわちxとyの足し算なのでどっちが「0」でも問題ありません。
こうするとx=aになります。

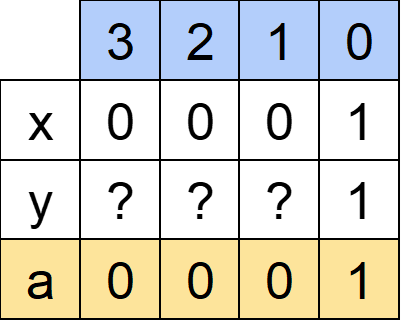
次にsの計算からyの値を考えていきます。
xが確定していればyの値も計算して確定できます。

実際に計算してみましょう。
i桁目は
「xのi桁目」+「yのi桁目」+「繰り上がり」で計算できます。

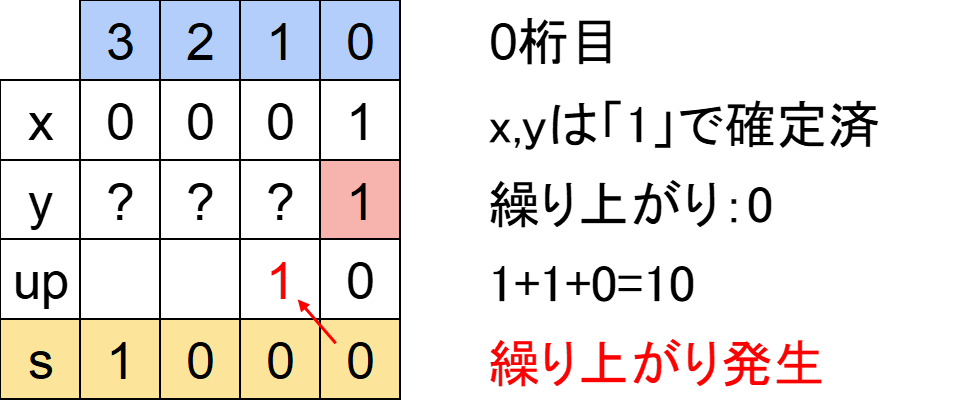
0桁目は「xの0桁目」「yの0桁目」がすでに「1」が確定しており、「繰り上がり」は「0」です。
「xの0桁目」+「yの0桁目」+「繰り上がり」
=1+1+0
=10
となります。
「10」の右端=「0」が「sの0桁目」に対応します。「sの0桁目」=「0」ですから問題ないです。
また、「10」ということは0桁目で繰り上がりが発生するので1桁目のupに繰り上がり「1」を書いておきます。

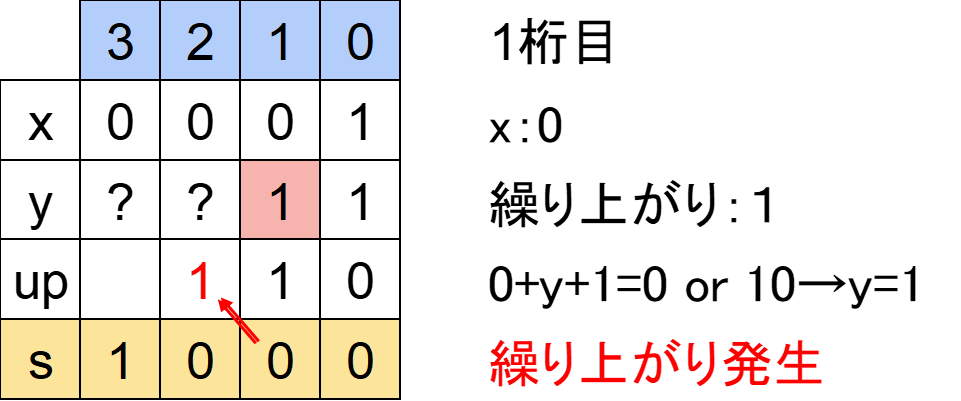
「yの1桁目」は「?」でした。また、0桁目で発生した繰り上がり「1」があります。
以下の式が成り立つようにyを決めます。
「xの1桁目」+「yの1桁目」+「繰り上がり」=「sの1桁目」
⇔0+y+1=0または10

この場合「yの1桁目」=「1」とすることで
「xの1桁目」+「yの1桁目」+「繰り上がり」
=0+1+1
=10
とできますから「yの1桁目」=「1」となります。
繰り上がりも発生するので、2桁目のupに記載しておきます。

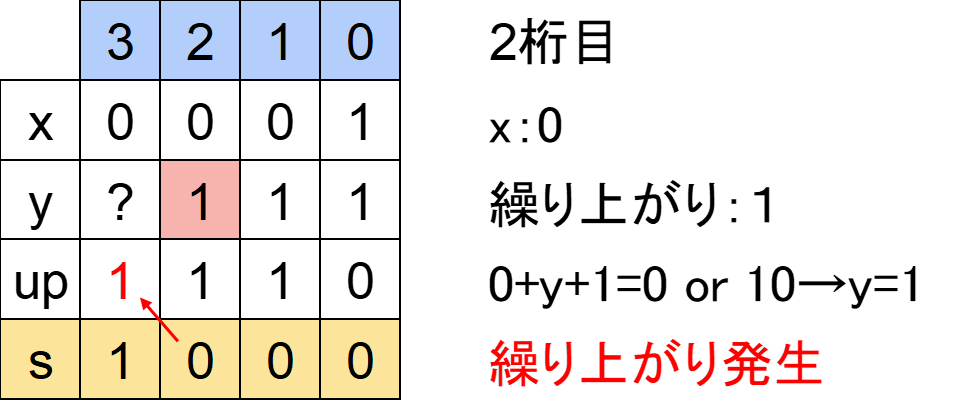
「yの2桁目」も「?」でした。また、1桁目で発生した繰り上がり「1」があります。
同様に式を立ててyを考えます。
「xの2桁目」+「yの2桁目」+「繰り上がり」=「sの2桁目」
⇔0+y+1=0または10

「yの2桁目」=「1」とすることで
「xの2桁目」+「yの2桁目」+「繰り上がり」
=0+1+1
=10
とできますから「yの2桁目」=「1」となります。
繰り上がりも発生するので、3桁目のupに記載しておきます。

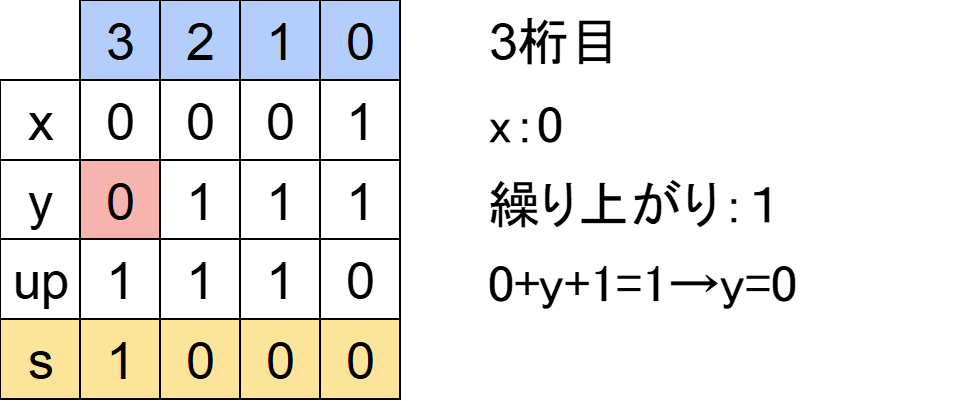
「yの3桁目」も「?」です。また、2桁目で発生した繰り上がり「1」があります。
「sの3桁目」は「1」なので
「xの3桁目」+「yの3桁目」+「繰り上がり」=「sの3桁目」
⇔0+y+1=1または11
となりそうです。

しかし「11」が入ってしまうとまた次の桁に繰り上がりが発生します。3桁目は最後の桁なので繰り上がりが発生すると困ります。
よって「11」はなしで「1」になるように式を立てます。
「xの3桁目」+「yの3桁目」+「繰り上がり」=「sの3桁目」
⇔0+y+1=1

y=0とすれば
「xの3桁目」+「yの3桁目」+「繰り上がり」
=0+0+1
=1
となります。

これでx=「0001」、y=「0111」とすれば条件を満たすことがわかりました。

ここまでの流れをおさらいしましょう。
(1)x AND y=a　の条件からx=aと決めてしまう
(2)x+y=sから繰り上がりを考慮しつつyの値を順に確定させる
これでyが確定できれば「Yes」になるわけです。
では「No」になるパターンはどのような場合でしょうか。

例えばa=「1010」、s=「0010」だった場合、同様にsからyを計算していくと3桁目で詰みます。

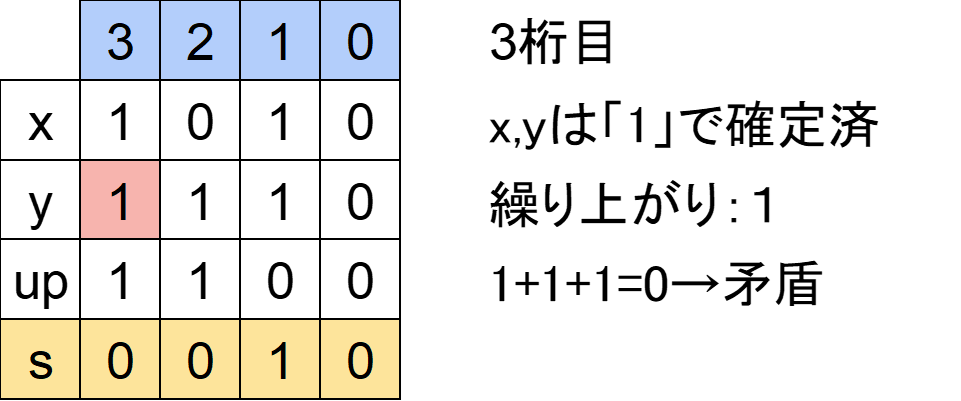
「xの3桁目」は「1」なので「yの3桁目」も「1」でなければなりません。
しかし「sの3桁目」は0です。
よって「xの3桁目」+「yの3桁目」+「繰り上がり」=「sの3桁目」となりません。(1+1+1≠0)
こうなったら「No」です。

「yのi桁目」の値は「xのi桁目」「繰り上がり」「sのi桁目」で決まります。
計算が合わなくなる　または　最後の桁で繰り上がりが発生する　と「No」です。
それぞれの値に対してyが「0」「1」どちらになるかを示したのが以下の表です。

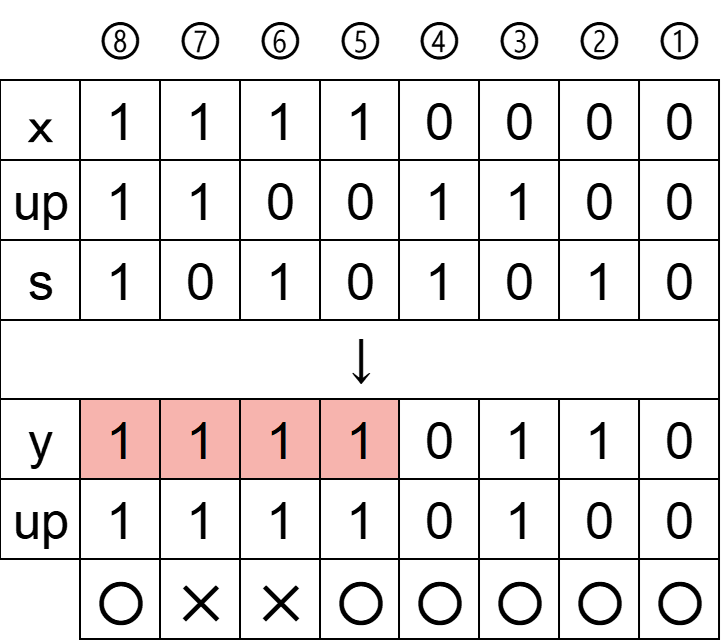
例えば⑤は
「xのi桁目」=1
「繰り上がり」=0
「sのi桁目」=0
のとき、
「yのi桁目」=1
で「xのi桁目」+「yのi桁目」+「繰り上がり」=1+1+0=10だから
「繰り上がり」=1が発生する
ということを示しています。

⑥と⑦は「xのi桁目」+「yのi桁目」+「繰り上がり」=「sのi桁目」にすることができません。なので最後の行に「✕」を書いています。
x AND y=aの条件からx=1のときは必ずy=1(赤色の部分)となることに注意してください。

ここから実装のテクニックを話します。
「xのi桁目」や「yのi桁目」はどのように確認すればよいでしょう。
これにはシフト演算とアンド演算を使います。

シフト演算とアンド演算
シフト演算をはbitを左右にずらす演算です。
例えば111001を右に3つずらすと
111001→000111
となります。
右端の「001」が消え、「111」が3つ分右に移動します。そうすると左が3つ分空くのでここに「000」を埋めるということです。

pythonでの右シフトの書き方は
「値」>>(シフト量)
となります。111001(=57)を右に3つずらす場合は
57>>3
と書きます。

シフト演算とアンド演算を組み合わせることで右からi桁目が「0」か「1」かを確認できます。
「111001」の3桁目が知りたいときはまず3つ右にシフト演算します。
「111001」→「000111」
そして「1」とアンド演算します。pythonでの書き方は「&」です。
「000111」&「1」=「1」
「1」になりました。これで右からi桁目が「1」とわかります。
もしi桁目が「0」ならアンド演算の結果も「0」になります。

まとめるとi桁目が「0」か「1」か知りたい場合は
(1)右にi個シフト演算
(2)「1」とアンド演算
を行えばよいです。

やることをまとめましょう。
(1)x=aとする
(2)「xのi桁目」「繰り上がり」「sのi桁目」から「yのi桁目」を計算
　・途中で計算が矛盾するか、最後の桁で繰り上がりが発生したら「No」
　・yが確定したら(最後まで計算できたら)「Yes」
計算量はテストケース一個あたりaまたはsの桁数のうち大きい方となります。
a,sは最大60桁で、テストケースは最大10^5個ですから全体の計算量は6010^5=610^6です。
pythonだとTLEしますがpypyなら間に合います。

これをそのままコードにしたのが【提出1】です。
これでもACなのですが、無駄が多いです。そもそもyiは管理する必要がありませんし、条件分岐もかっこよくないです。
なのでもうちょっと綺麗にしたのが【提出2】です。やってることは同じです。

【提出1】

# pypyで提出

# 入力の受け取り
N=int(input())

# 各テストケース
for T in range(N):
    # 入力の受け取り
    a,s=map(int,input().split())
    # x=aにする
    x=a
    # 「繰り上がり」
    up=0
    # 詰んでいないかの判定
    OK=True
    # s,aのうち桁数の大きい方
    bit_len=max(a.bit_length(),s.bit_length())

    # i桁目
    for i in range(bit_len):
        # 「xのi桁目」
        xi=x>>i & 1
        # 「sのi桁目」
        si=s>>i & 1

        # 「yのi桁目」と「繰り上がり」を計算
        if xi==0 and up==0 and si==0:
            yi=0
            up=0
        elif xi==0 and up==0 and si==1:
            yi=1
            up=0
        elif xi==0 and up==1 and si==0:
            yi=1
            up=1
        elif xi==0 and up==1 and si==1:
            yi=0
            up=0
        elif xi==1 and up==0 and si==0:
            yi=1
            up=1
        elif xi==1 and up==0 and si==1:
            yi=1
            up=1
            OK=False
            break
        elif xi==1 and up==1 and si==0:
            yi=1
            up=1
            OK=False
            break
        elif xi==1 and up==1 and si==1:
            yi=1
            up=1
        
        # 最後の桁で「繰り上がり」があれば
        if i==bit_len-1 and up==1:
            OK=False
    
    # OKがFalseに変わっていなければ
    if OK==True:
        print("Yes")
    else:
        print("No")

【提出2】

# 入力の受け取り
N=int(input())

# 各テストケース
for T in range(N):
    # 入力の受け取り
    a,s=map(int,input().split())
    up=0
    # 詰んでいないかの判定
    OK=True
    # s,aのうち桁数の大きい方
    bit_len=max(a.bit_length(),s.bit_length())

    # i桁目
    for i in range(bit_len):
        # 「aのi桁目」
        ai=a>>i & 1
        # 「sのi桁目」
        si=s>>i & 1

        # 条件から繰り上がりを計算
        if ai==0:
            if up==1 and si==0:
                up=1
            else:
                up=0
        else:
            if up+si==1:
                OK=False
                break
            up=1    
        
        # 最後の桁で「繰り上がり」があれば
        if i==bit_len-1 and up==1:
            OK=False
    
    # OKがFalseに変わっていなければ
    if OK==True:
        print("Yes")
    else:
        print("No")

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】