ABC236 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC236(AtCoder Beginner Contest 236)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - chukodai

問題文の通り、a文字目とb文字目を入れ替えて出力します。

手順は以下です。
①入力の受け取り
②一文字ずつリストへ格納
③a文字目とb文字目を入れ替え
④リストを結合
⑤答えを出力

①入力の受け取り
S,a,bを受け取ります。
Sは文字列、a,bは整数として受け取ります。

②一文字ずつリストへ格納
Sを一文字ずつリストへ格納します。
list(文字列)
と書くことで一文字ずつリストへ格納されます。
S_listというリストへ格納しましょう。

③a文字目とb文字目を入れ替え
pythonでは0インデックス(先頭が0、次が1、...)となっているので問題文でいうa,b文字目とリストのインデックス番号で言うa,b文字目が1ずれます。
よってa,bを予めマイナス1します。
例：a=1,b=5の場合、入れ替えるのはS_listの0番目とS_listの4番目です。

リストのx番目は
リスト[x]
と書きます。

S_listのa,b番目の要素を入れ替えます。
x,yを入れ替えるときは以下のように書くと楽です。
x,y=y,x
よってS_listのa番目とb番目を入れ替える場合以下のようになります。
S_list[a],S_list[b]=S_list[b],S_list[a]

④リストを結合
入れ替えが出来たらリストを結合します。
リストの結合は以下のように書きます。
"".join(リスト)
少々分かりづらい書き方ですが、「python リスト 結合」などで検索すればすぐに出てくるのでいちいち覚える必要はありません。

⑤答えを出力
結合したリストを出力すれば終わりです。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# ①入力の受け取り
S=input()
a,b=map(int,input().split())

# ②一文字ずつリストへ格納
S_list=list(S)

# 0インデックスのためマイナス1してずらす
a-=1
b-=1

# ③a文字目とb文字目を入れ替え
S_list[a],S_list[b]=S_list[b],S_list[a]

# ④リストを結合
ans="".join(S_list)

# ⑤答えを出力
print(ans)

B - Who is missing?

1,2,...,Nのカードが何枚ずつあるか確認するリストを用意し、記録します。
Aの要素を一つずつ見ていって対応する要素をカウント(プラス1)していきます。

1,2,...,Nのカードについてカウントした枚数を確認していきます。
3枚しかないものが答えです。

答えを見つけたら出力して終了します。
途中で終了する場合は
exit()
と書きます。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))

# 枚数を数えるリスト
count=[0]*(N+1)

# i=0~(4N-2)
for i in range(4*N-1):
    # A[i]をプラス一枚カウント
    count[A[i]]+=1

# i=1~N
for i in range(1,N+1):
    # 枚数が3ならば
    if count[i]==3:
        # iが抜かれたカード
        print(i)
        # 途中終了
        exit()

C - Route Map

Sの各駅についてTに含まれるか確認すればOKです。

連想配列(defaultdict)を使ってTに含まれる要素を記録し、確認します。
連想配列(defaultdict)を使ったことがない人は以下を参照してください。

defaultdict(連想配列)について
辞書または連想配列と言います。
キー：値
というような対応付を行えるデータ構造です。
連想配列はdict()と書くことでも使えますが、デフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import：from collections import defaultdict
作成(デフォルト0)：変数名=defaultdict(int)
キー、値の登録：変数名[キー]=値
値の取り出し：変数名[キー]
【使用例】

# インポート
from collections import defaultdict

# 作成(デフォルト0)：変数名=defaultdict(int)
dictionary=defaultdict(int)

# キー、値の登録：変数名[キー]=値
dictionary[5]=1

# 値の取り出し：変数名[キー]
x=dictionary[5]

詳しく知りたい人は以下を参照してください。

Tに含まれる駅は連想配列に「1」を記録しておきます。
Sの各駅について
・連想配列の値が「1」→止まる(Yes)
・連想配列の値が「0」(デフォルトの値)→止まらない(No)
となります。

【提出】

# 入力の受け取り
N,M=map(int,input().split())
S=list(map(str,input().split()))
T=list(map(str,input().split()))

# defaultdictをインポート
from collections import defaultdict

# 急行が止まる駅
# 「1」なら止まる
# 「0」(デフォルトの値)なら止まらない
stations=defaultdict(int)

# i=0~(M-1)
for i in range(M):
    # 「1」を記録
    stations[T[i]]=1

# i=0~(N-1)
for i in range(N):
    # S[i]が止まる駅
    if stations[S[i]]==1:
        # 「Yes」を出力
        print("Yes")
    # 止まらない駅
    else:
        # 「No」を出力
        print("No")

D - Dance

まず2N人から2人組を作る組み合わせ数がいくつあるか考えてみましょう。
Nが最大の8のとき、2N=16です。
この16人に対してAというカードを2枚、Bというカードを2枚、...、Hというカードを2枚配ることを考えます。
同じカードを持っている人がペアです。(例えば1番と5番がAを持っていたら二人はペアです)

配り方はAABB...HHの順列の数に一致するので16!/(2!2!...2!)=16!/2^8となります。
さらにカードは区別する必要がないのでA,B,...,Hの順列分、すなわち8!で割ります。
結果として2人組を作る組み合わせ数は最大で
(16!/(2^8))*(1/8!)=2027025≒2*10^6
となります。全探索はpythonでは無理そうですがpypyならぎりぎり間に合いそうかなーくらいですね。

次にどうやって全てのペアを列挙するか考えます。
単純にitertoolsで1~2Nの順列を作って(0番目と1番目),(2番目と3番目),...,((2N-2)番目と(2N-1))をペアとしたいところですが、ペアの重複が発生するためうまくいきません。

そこで以下のように考えます。
①pairsというリストを作る(最終的にpairsの(0番目と1番目),(2番目と3番目),...,((2N-2)番目と(2N-1))をペアとする)
②・pairsの偶数番目の人を追加する時(pairs[0],pairs[2],...にあたる人)
　　残った人の中で一番番号の小さい人を追加する
　・pairsに奇数番目の人を追加する時(pairs[1],pairs[3],...にあたる人)
　　残った人の誰かを選んで追加する(総当りで試す)
③pairsの人数が２Nになったら「楽しさ」を計算

実装には再起関数とDFS(深さ優先探索)を使います。
DFSはグラフを探索するアルゴリズムですが、本問のように総当りしたいときに応用がききます。

まず「相性」は入力のままだと使い勝手が悪いので表形式にしましょう。
以下のように受け取りします。

# 入力の受け取り
N=int(input())

# 「相性」の表
A=[[0]*(2*N+1) for i in range(2*N+1)]

# i=1~(2N-1)
for i in range(1,2*N):
    # 入力を受け取る
    tmp=list(map(int,input().split()))
    # 表に記載
    for j in range(len(tmp)):
        A[i][j+(i+1)]=tmp[j]
        A[j+(i+1)][i]=tmp[j]

例えば入力例1の場合だとAは以下のようになります。

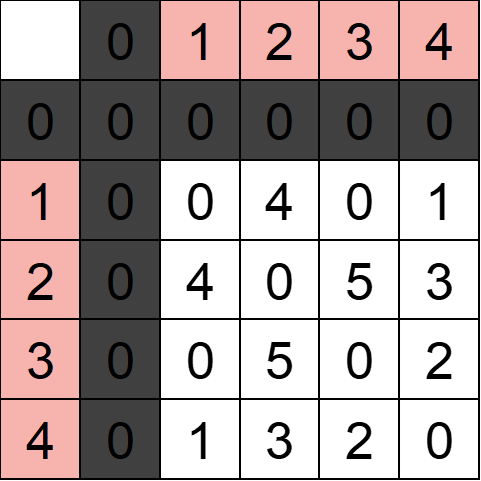
例えば1番と4番の相性はA[1][4]=1と確認できます。

続いて2つのリストを作ります。
・selected：すでに選ばれているか(pairsの中に入っているか)管理するリスト
　selected[x]=Falseならxは選ばれていない、Trueならすでに選ばれている
・pairs：ペアになる人を記録するリスト(最初は空)
　最終的にpairsの(0番目と1番目),(2番目と3番目),...,((2N-2)番目と(2N-1))をペアとする

ここまでできたらDFSで全ての組を作って確認します。
再帰関数を使って実装します。

まず関数DFSを作ります。
引数はselectedとpairsです。

「関数DFSの処理」
・次にpairsへ追加する人が偶数番目⇔pairsの長さが偶数
　selectedがFalseの中で一番番号の小さい人をpairsに追加
・次にpairsへ追加する人が奇数番目⇔pairsの長さが奇数
　selectedがFalseの人を順番にpairsへ追加
どちらの操作を行った場合でもpairs,selectedを更新し、次のDFSを始めます。
・pairsの長さが2N
　各ペアの「相性」から「楽しさ」を計算
　そこまでに計算した「楽しさ」より大きければ答えを更新

処理が終わったら答えを出力します。
Pythonでは間に合わないのでpypyで提出します。

再帰関数をあまり使ったことがない人は挙動がイメージしづらいと思います。
本問についてではないですが、DFS、再帰関数について解説した動画がありますのでまずそちらをご覧ください。

その後【提出】の内容をコピペしてコードエディタのステップ実行機能を使い、どのような挙動をするか確認しましょう。

だいたい流れがわかったら今度は自力で書いてみましょう。
本問が難しければDFSの練習としてより簡単なABC213Dを先にやってみるのが良いです。

再帰関数ははじめはよくわからない、書けないという人が多いと思います。
ですがこれを使えると他の様々な問題に応用がきき、レーティングも上がっていくので頑張って自分のものにしましょう。

【提出】

# pypyで提出

# 再起回数上限を10^6へ変更
import sys
sys.setrecursionlimit(10**6)

# 入力の受け取り
N=int(input())

# 「相性」の表
A=[[0]*(2*N+1) for i in range(2*N+1)]

# i=1~(2N-1)
for i in range(1,2*N):
    # 入力を受け取る
    tmp=list(map(int,input().split()))
    # 表に記載
    for j in range(len(tmp)):
        A[i][j+(i+1)]=tmp[j]
        A[j+(i+1)][i]=tmp[j]

# 答え
ans=0

# 引数：selected(すでに選ばれている人)　pairs(ペアの一覧)
def DFS(selected,pairs):
    # ansを更新できるように
    global ans

    # 全員ペアができていれば
    # ⇔pairsの長さが2Nならば
    if len(pairs)==2*N:
        # 「楽しさ」の計算
        score=0
        # i=0~(2N-1)まで　2毎に増加
        for i in range(0,2*N,2):
            # ペアになる人
            x=pairs[i]
            y=pairs[i+1]
            # 「相性」から「楽しさ」を計算
            score^=A[x][y]
        
        # 「楽しさ」が大きかったら答えを更新
        ans=max(ans,score)

    # 次に追加する人が偶数番目
    # ⇔pairsの長さが偶数
    elif len(pairs)%2==0:
        # 選ばれていない中で一番小さい番号の人を選ぶ
        i=1
        while selected[i]==True:
            i+=1
        # pairsへ追加
        pairs.append(i)
        # 選択済みにする
        selected[i]=True
        # 次のDFSへ
        DFS(selected,pairs)
        # 前のDFSが終わったらpairsから消す
        pairs.pop()        
        # selectedをFalseへ変更
        selected[i]=False


    # 次に追加する人が奇数番目
    # ⇔pairsの長さが奇数
    else:
        # 選ばれていない人を一人ずつ全て選ぶ
        for i in range(1,2*N+1):
            # まだ選ばれていないなら
            if selected[i]==False:
                # 追加
                pairs.append(i)
                # 選択済みにする
                selected[i]=True
                # 次のDFSへ
                DFS(selected,pairs)
                # 前のDFSが終わったらpairsから消す
                pairs.pop()        
                # selectedをFalseへ変更
                selected[i]=False

# すでに選ばれているか(pairsの中に入っているか)管理するリスト
# =Falseなら選ばれていない、Trueならすでに選ばれている
# 最初は誰も選ばれていない
selected=[False]*(2*N+1)

# ペアになる人を記録するリスト(最初は空)
# 最終的にpairsの(0番目と1番目),(2番目と3番目),...,((2N-2)番目と(2N-1))をペアとする
pairs=[]

# DFSを開始
DFS(selected,pairs)

# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】