ABC319 A~D問題の解説記事です。
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
A
めんどくさいですが素直にifを並べて解きましょう。
Sが◯◯だったら→〇〇を出力という処理をひたすら書けばOKです。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出】
# 入力の受け取り
S=input()
# S="tourist"ならば
if S=="tourist":
print(3858)
elif S=="ksun48":
print(3679)
elif S=="Benq":
print(3658)
elif S=="Um_nik":
print(3648)
elif S=="apiad":
print(3638)
elif S=="Stonefeang":
print(3630)
elif S=="ecnerwala":
print(3613)
elif S=="mnbvmar":
print(3555)
elif S=="newbiedmy":
print(3516)
elif S=="semiexp":
print(3481)
B
問題文が何言ってるかよくわかりませんね。
とりあえず入力例1を見ながら何をすればいいか確認しましょう。
【例】
N=12
まずiを決めて固定します。
・i=0の場合
1以上9以下のNの約数jであって、0がN/jの倍数であるものが存在するとき、そのようなjのうち最小のものに対応する数字をs0とする。
jは1以上9以下らしいです。順番に確認してみます。
j=1:N/j=12/1=12 ⇔ ◯:i=0が12の倍数
j=2:N/j=12/2=6 ⇔ ◯:i=0が6の倍数
j=3:N/j=12/3=4 ⇔ ◯:i=0が4の倍数
j=4:N/j=12/4=3 ⇔ ◯:i=0が3の倍数
j=5:N=12の約数でない
j=6:N/j=12/6=2 ⇔ ◯:i=0が2の倍数
j=7:N=12の約数でない
j=8:N=12の約数でない
j=9:N=12の約数でない
「0がN/jの倍数」の倍数になっているものはj=1,2,3,4,6があります。
このうち一番小さいのはj=1です。つまりs0=1になります。
・i=4の場合
1以上9以下のNの約数jであって、4がN/jの倍数であるものが存在するとき、そのようなjのうち最小のものに対応する数字をs4とする。
j=1:N/j=12/1=12 ⇔ ✕:i=4が12の倍数でない
j=2:N/j=12/2=6 ⇔ ✕:i=4が6の倍数でない
j=3:N/j=12/3=4 ⇔ ◯:i=4が4の倍数
j=4:N/j=12/4=3 ⇔ ✕:i=4が3の倍数でない
j=5:N=12の約数でない
j=6:N/j=12/6=2 ⇔ ◯:i=4が2の倍数
j=7:N=12の約数でない
j=8:N=12の約数でない
j=9:N=12の約数でない
「4がN/jの倍数」の倍数になっているものはj=3,6があります。
このうち一番小さいのはj=3です。つまりs4=3になります。
このように上記でやっているチェックをi=0,1,2,...,NについてすべてやっていけばOKです。
【提出】
# 入力の受け取り
N=int(input())
# 答え
s=""
# i=0~N
for i in range(N+1):
# j=1~9
for j in range(1,10):
# jがNの約数であれば⇔Nがjで割り切れれば
if N%j==0:
# N/jがiの倍数であれば⇔iがN/jで割り切れれば
if i%(N//j)==0:
# 答えに追加
s+=str(j)
# forを抜ける
break
# 長さがi+1以下ならば(jが存在しなかった場合)
if len(s)<i+1:
# 「-」を追加
s+="-"
# 答えの出力
print(s)
C
問題の意味がよく分からなければ紙にてきとうな数字を書いて何をしているのか試してみましょう。
要するにこれは少し変則的なビンゴゲームを高橋くんがやっているという状況です。
(ただし、問題の条件にあるようにビンゴすることはありません)
マスは9個で開く(高橋くんが数字を知る)順番はランダムなので、開く順番の場合の数は9!=362880通りあります。
これくらいなら全探索しても間に合いそうです。
1個マスを開く度に高橋くんががっかりするかを確認します。
例えば以下のようにマスへ番号を振った場合を考えます。
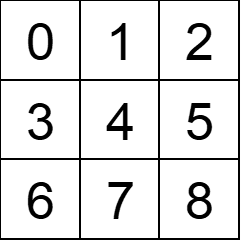
一番上の行であれば
・0番と1番が開いている かつ それらが同じ番号
・2番はまだ開いていない
という状況でがっかりします。(2番が0番、1番と同じ番号になることはありません)
0,1,2は番号を入れ替えても同じです。
これをすべての行、列、ななめについて毎回確認するわけです。
【提出】では以下のように処理を行っています。
(1)最初にビンゴの数字を10,11,12,13,...と初期化しておく。9より大きい番号はまだ開いていないという意味。
(2)マスを開く順番をitertoolsで全通り作る
(3)一つ開くごとに高橋くんががっかりしているかを確認する。がっかりしていたら次の順番へ
(4)全てのパターンのうち、がっかりしていないパターンの個数から確率を計算する
itertools
itertoolsは数列の順列や組み合わせなどを作ることができるライブラリです。
「使い方」
import:import itertolls
順列:permutations(range(始まり,終わり+1))
重複なしの組み合わせ:combinations(range(始まり,終わり+1),取る個数)
重複ありの組み合わせ:combinations_with_rep(range(始まり,終わり+1),取る個数)
直積:product(range(始まり,終わり+1),range(始まり,終わり+1)):
「使用例」
# import:import itertolls
import itertools
N,K=4,2
# 順列:permutations(range(N))
# seq=(0,1,2,3),(0,1,3,2),(0,2,1,3),(0,2,3,1),...,(3,2,1,0)
print("[順列]")
for seq in itertools.permutations(range(N)):
print(seq)
# 重複なしの組み合わせ:combinations(range(N),K)
print("[重複なしの組み合わせ]")
# seq=(0,1),(0,2),(0,3),(1,2)...,(2,3)
for seq in itertools.combinations(range(N),K):
print(seq)
# 重複ありの組み合わせ:combinations_with_rep(range(N),K)
print("[重複ありの組み合わせ]")
# seq=(0,0),(0,1),(0,2),(0,3),(1,1)...,(3,3)
for seq in itertools.combinations_with_replacement(range(N),K):
print(seq)
# 直積:product(range(N),range(N)):
print("[直積]")
# seq=(0,0),(0,1),(0,2),(0,3),(1,0)...,(3,3)
for seq in itertools.product(range(N),range(N)):
print(seq)
ただのPythonだと間に合わないのでpypyを選択して提出します。
【提出】
# pypyで提出
# 番号の受け取り
c=[0,0,0,0,0,0,0,0,0]
c[0],c[1],c[2]=map(int, input().split())
c[3],c[4],c[5]=map(int, input().split())
c[6],c[7],c[8]=map(int, input().split())
# 高橋くんががっかりしているか確認する関数
def Judge():
# 行方向
# x=0,3,6
for x in (0,3,6):
# 左と中央が同じ かつ 右が開いていない
if B[x]==B[x+1] and 9<B[x+2]:return True
# 中央と右が同じ かつ 左が開いていない
if B[x+1]==B[x+2] and 9<B[x]:return True
# 左と右が同じ かつ 中央が開いていない
if B[x+2]==B[x] and 9<B[x+1]:return True
# 列方向
# x=0,1,2
for x in (0,1,2):
# 上と中央が同じ かつ 下が開いていない
if B[x]==B[x+3] and 9<B[x+6]:return True
# 中央と右が同じ かつ 上が開いていない
if B[x+3]==B[x+6] and 9<B[x]:return True
# 下と上が同じ かつ 中央が開いていない
if B[x+6]==B[x] and 9<B[x+3]:return True
# 左上→右下斜め方向
if B[0]==B[4] and 9<B[8]:return True
if B[4]==B[8] and 9<B[0]:return True
if B[8]==B[0] and 9<B[4]:return True
# 右上→左下斜め方向
if B[2]==B[4] and 9<B[6]:return True
if B[4]==B[6] and 9<B[2]:return True
if B[6]==B[2] and 9<B[4]:return True
# がっかりしていなかったらFalseを返す
return False
# がっかりしていないパターン数
count=362880
# itertoolsのインポート
import itertools
# 0~9の順列の作成
for p in itertools.permutations(range(9)):
# ビンゴカードを作る(9より大きい数字は開いていない)
B=[10,11,12,13,14,15,16,17,18,19]
# がっかりしているか
Gakkari=False
# i番目に開いた数字
# i=0~8
for i in range(9):
# p[i]番の番号を開く
B[p[i]]=c[p[i]]
# がっかりしていたら
if Judge()==True:
Gakkari=True
# forを抜ける
break
# がっかりしていたら
if Gakkari==True:
# カウントを減らす
count-=1
# 確率を出力
print(count/362880)
D
競プロでよく使う考え方に「答えを決め打ちしてそれが達成可能か確認する」という方法があります。
横幅Wを決めてしまえば行数M以内で文字を表示できるかは簡単に確認できます。実際に並べてみれば良いわけですから、この確認はO(N)で出来ます。
ですので達成可能なWのうち最小のものを二分探索で探せばOKです。
二分探索
二分探索は区間の中央の値が条件を満たすか確認し、徐々に区間を狭めて目的の値を得るアルゴリズムです。
探索を行う前に対象の数列は単調増加、または減少となっている必要があります。
(1)区間[左,右]を指定する
左=最小値(単調減少なら最大値)のインデックス番号
右=最大値(単調減少なら最小値)のインデックス番号
(2)中央=(左+右)//2が条件を満たすか確認
(3)(2)の結果より左または右を更新する
・中央が条件を満たす:右(または左)=中央と更新
・中央が条件を満たさない:左(または右)=中央と更新
(4)1<(右-左)となっている間(2)~(4)を繰り返す
【提出】
# 入力の受け取り
N,M=map(int, input().split())
L=list(map(int, input().split()))
# 幅Wが達成可能か確認する関数
def Judge(W):
# 文字数
Mozi=0
# 行数
Gyou=1
# iを初期化
i=0
# i<Nの間
while i<N:
# 次の文字が同じ行に配置できないなら
# ⇔W<「これまでの文字数」+「次の文字数」
if W<Mozi+L[i]:
# 行を増やす⇔次の行へ
Gyou+=1
# 文字数を0にする
Mozi=0
# 次の文字が同じ行に配置できるなら
# ⇔「これまでの文字数」+「次の文字数」≦W
if Mozi+L[i]<=W:
# 文字を配置⇔文字数を増やす
Mozi+=L[i]+1
# 次の文字へ
i+=1
# 行数がM以下なら
if Gyou<=M:
# Trueを返す
return True
# そうでなければ
else:
# Falseを返す
return False
# 右(Lの最大値-1)
l=max(L)-1
# 左(大きな数)
r=10**20
# 1<右-左 の間
while 1<r-l:
# 中央=(左+右)/2
c=(l+r)//2
# W=中央が達成可能なら
if Judge(c):
# 右=中央
r=c
# 達成不可能なら
else:
# 左=中央
l=c
# 答えの出力
print(r)