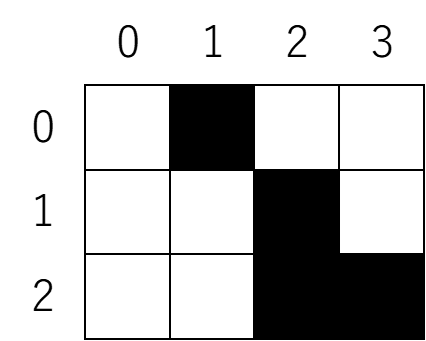M-SOLUTIONS プロコンオープン2021(ABC232) A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

M-SOLUTIONS プロコンオープン2021(AtCoder Beginner Contest 232)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

M-SOLUTIONS様について

本コンテストはM-SOLUTIONS株式会社様が主催されています。

公式ホームページ

求人(要求ランクD以上のため、茶色コーダーの方でも応募可能です)

A - QQ solver

Sを文字列として受け取り、1文字目と3文字目を掛け算して出力します。

以下に注意しましょう。

・pythonは0インデックス

pythonではSの1文字目をS[0]、2文字目をS[1]...と表し、インデックス番号がずれます。
このようなインデックスの振り方を0インデックスと呼びます。

よって
1文字目=S[0]
3文字目=S[2]
となります。

・文字列→整数へ変換する
文字列として受け取ったものをそのまま掛け算すると、文字同士の計算のためエラーになります。
先に文字列→整数へ変換する必要があります。
文字列を整数へ変換するには以下のように書きます。
int (文字列)

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
S=input()

# Sの0文字目と2文字目を整数へ変換
S0=int(S[0])
S2=int(S[2])

# 掛け算して出力
print(S0*S2)

B - Caesar Cipher

kは0～25のどれかになります。
k=26～は1周して元に戻るからです。
(「a」の1個後ろも27個後ろも「b｣となる)
26通りしかないのであればkを全通り試せばいいです。

x個後ろの文字をどのように変換するか考えます。

PCで扱う文字には「文字コード」という番号がついています。文字コードは
「a」=97
「b」=98
...
「Z」=122
と連番になっています。

「文字コード」と「文字」は相互に変換可能です。
以下のように書くことで変換ができます。
ord(「文字」)→「文字コード」
chr(「文字コード」)→「文字」

ある文字を×個後ろの文字へ変換するなら以下の手順でできそうです。
(1)「文字」→「文字コード」に変換
(2)「文字コード」+x
(3)「文字コード」→「文字」へ変換

例えば「a」を3個後ろの文字へ変換したければ以下の手順を踏みます。
(1)「a」を「文字コード」へ変換(=97)
(2)「文字コード」+3=97+3=100
(3)「文字コード」→「文字」へ変換(「文字コード」100=「d」)

しかし｢z」より後の文字列だと「a」に戻ってくるところが厄介です。
例えば｢z」(「文字コード」122)を3個後ろの文字(「c」)へ変換するならば
「z」の「文字コード」+3=122+3=125 → 99=｢c｣
としなければならないわけです。

そこで×を足すときに26で割った余りを使います。以下の式で計算します。
「変換先文字コード」=(「変換元文字コード｣-97+x)%26+97

具体例でみてみましょう。
｢z」(「文字コード」122)を3個後ろの文字へ変換する場合
「変換先文字コード」=(122-97+3)%26+97=28%26+97=2+97=99
ちゃんと「文字コード」99、すなわち「c」に変換できました。

あとはTの各文字について上記の式を使って変換し、Sと一致するか確認すればOKです。
一致したら「Yes」を出力して途中終了します。
途中終了はexit()と書きます。

【提出】

# 入力の受け取り
S=input()
T=input()

# k=0~25
for k in range(26):
    # 変換後のT
    T_conv=""

    # i=0~(Tの文字数-1)
    for i in range(len(T)):
        # 「文字」→「文字コード」
        # "a"は97,"b"は98,...
        code=ord(T[i])
        # k個後ろの文字へ変換
        # 「変換先文字コード」=(「変換元文字コード｣-97+x)%26+97
        code_conv=(code+k-97)%26+97
        # 「文字コード」→「文字」
        T_conv+=chr(code_conv)

    # SとTの変換後が一致したら
    if S==T_conv:
        # 「Yes」を出力
        print("Yes")
        # 途中終了
        exit()

# 「No」を出力
print("No")

C - Graph Isomorphism

なにやら問題文がごちゃごちゃしていて分かりづらいですが、要するに青木君のおもちゃについているボールについて、

1→3
2→7
...

というような感じで適当に番号を変換し、高橋君のおもちゃと一致するか、すなわち入力が一致するかを検証します。

ここから実装に合わせて0インデックス、すなわち問題文でいう1番のボールを⓪、2番のボールを①、...として説明します。

どのおもちゃがつながっているかは二次元配列で管理しましょう｡
高橋君のおもちゃについて、どのボールがつながっているかを管理するリストをtakahashiとします。
例えば高橋君のおもちゃについて
⓪と①
③と④
⑤と①
がつながっている場合、takahashiは以下のようになります。
takahashi=[[1],[0,5],[],[4],[3],[1]]
つまり以下のようになっています。
takahashi[0]=[1]
takahashi[1]=[0,5]
takahashi[2]=[]
takahashi[3]=[4]
takahashi[4]=[3]
takahashi[5]=[1]

どの番号に変換すればいいか？は制約が1≤N≤8と小さいので全探索できます。

P=(0~(N-1))の順列として
⓪→P[0]
①→P[1]
...
と変換します。
例えばP=[2,4,1,5,6,3,7,0]であれば以下のように変換します。
⓪→②
①→④
②→①
③→⑤
④→⑥
⑤→③
⑥→⑦
⑦→⓪

N=8となる場合のP、すなわちP=[0,1,2,3,4,5,6,7]を並び替える場合でも、順列はたかだか8!=40320通りしかありません。
これなら全順列を試しても実行制限時間に間に合います。

順列を作るにはitertoolsを使うと便利です。
0～(N-1)の順列が欲しいので、permutationsを使います。
itertoolsを使ったことがない人は以下をご覧ください。

itertools
itertoolsは数列の順列や組み合わせなどを作ることができるライブラリです。
「使い方」
import：import itertolls
順列：permutations(range(始まり,終わり+1))
重複なしの組み合わせ：combinations(range(始まり,終わり+1),取る個数)
重複ありの組み合わせ：combinations_with_rep(range(始まり,終わり+1),取る個数)
直積：product(range(始まり,終わり+1),range(始まり,終わり+1)):

「使用例」
以下をまるごとコピペして実行してみましょう。

# import：import itertolls
import itertools
 
N,K=4,2
 
# 順列：permutations(range(N))
# seq=(0,1,2,3),(0,1,3,2),(0,2,1,3),(0,2,3,1),...,(3,2,1,0)
print("[順列]")
for seq in itertools.permutations(range(N)):
    print(seq)
 
# 重複なしの組み合わせ：combinations(range(N),K)
print("[重複なしの組み合わせ]")
# seq=(0,1),(0,2),(0,3),(1,2)...,(2,3)
for seq in itertools.combinations(range(N),K):
    print(seq)
 
# 重複ありの組み合わせ：combinations_with_rep(range(N),K)
print("[重複ありの組み合わせ]")
# seq=(0,0),(0,1),(0,2),(0,3),(1,1)...,(3,3)
for seq in itertools.combinations_with_replacement(range(N),K):
    print(seq)
 
# 直積：product(range(N),range(N)):
print("[直積]")
# seq=(0,0),(0,1),(0,2),(0,3),(1,0)...,(3,3)
for seq in itertools.product(range(N),range(N)):
    print(seq)

itertoolsでPを作ってから高橋君の入力と青木君の変換した入力が一致するか確認します。
ただし、二次元配列の一致判定は順序が揃っているかもチェックされます。入力を受け取った後要素ごとにソートしておきましょう。

【提出】

# 入力の受け取り
# 入力の受け取り
N,M=map(int,input().split())

# 高橋くんのおもちゃ：つながっているボール
takahashi=[[] for i in range(N)]

# M回
for i in range(M):
    # 入力の受け取り
    A,B=map(int,input().split())
    # 0インデックスにするため-1
    A-=1
    B-=1
    # つながっているボールを記録
    takahashi[A].append(B)
    takahashi[B].append(A)

# 配列の各要素について順番を小さい順にソート
for i in range(N):
    takahashi[i].sort()

# 青木くんのおもちゃ：つながっているボールの情報
Aoki_edge=[]

# M回
for i in range(M):
    # 入力の受け取り
    C,D=map(int,input().split())
    # 0インデックスにするため-1
    C-=1
    D-=1
    # 情報を記録
    Aoki_edge.append([C,D])

# itertoolsをインポート
import itertools

# 順列の作成
# 例：N=4
# P=(0, 1, 2, 3), (0, 1, 3, 2), (0, 2, 1, 3),...,(3, 2, 1, 0)
for P in itertools.permutations(range(N)):
    # 青木くんのおもちゃ：つながっているボール
    Aoki=[[] for i in range(N)]

    # C,Dを取り出し
    for C,D in Aoki_edge:
        # 変換
        C_conv=P[C]
        D_conv=P[D]
        # 格納
        Aoki[C_conv].append(D_conv)
        Aoki[D_conv].append(C_conv)

    # 配列の各要素について順番を小さい順にソート
    for i in range(N):
        Aoki[i].sort()

    # おもちゃが一致したら
    if takahashi==Aoki:
        # 「Yes」を出力
        print("Yes")
        # 途中終了
        exit()

# 「No」を出力
print("No")

D - Weak Takahashi

BFSを使います。

本問についてではないですが、BFSのやり方については動画を作成しているので是非ご覧ください。

各マスについてそこに至るまでに最大何マスを通っているか記録していきましょう。

例えば入力例1は図にすると以下のようになります。
※1行目を0、2行目を1、...と0インデックスで表記しています。列も同様です。

各マスに「そこに至るまでに最大何マスを通れるか」を記録していきます。
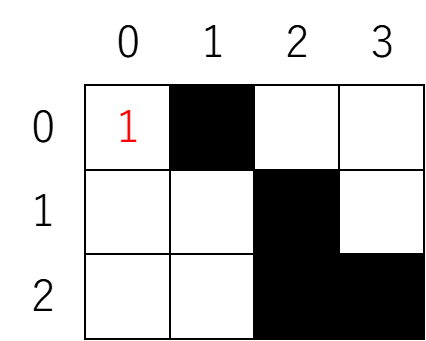
まずスタート地点は「1」です。

スタート地点の下マス、右マスが壁でなければ進めます。
この場合は下マスのみ壁でないので進めます。
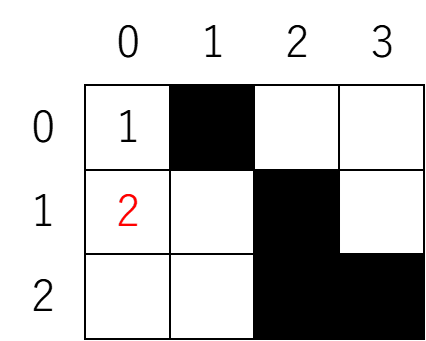
進んだら(「今いるマス」+1)を記録します。

また進んだマスで同じことを繰り返します。
すなわち下マス、右マスが壁でなければ(「今いるマス」+1)を記録していきます。
もしすでにマスに数字が埋まっていれば、(マスに書いている数)<(「今いるマス」+1)の場合のみ数字を更新します。

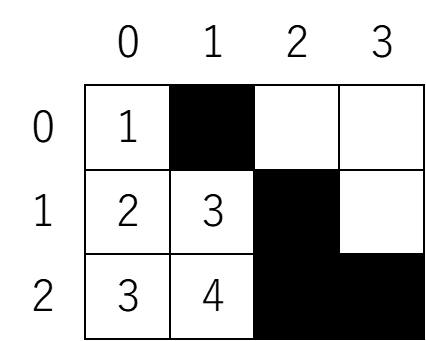
全部埋めると以下のようになります。

あとはマスに書いている数のうち、一番大きな数を出力して終わりです。

マスを順に探索するためにBFS(幅優先探索)を使います。BFSはグラフを探索するアルゴリズムです。

具体的な手順は以下です。
※キューがよくわからない人は後述の「dequeについて」を見てください。
(1)キューに(0,0)(=スタート地点)を入れる
(2)キューから要素を取り出す(=「今いるマス」の(行,列))
(3)「今いるマス」の数字を確認する
(4)下マス(行+1,列)について
　・グリッドを飛び出していない(行+1<H)　かつ　壁でない　場合
　　・(下マスに書いている数)く(「今いるマス」+1)であれば
　　　下マスに(「今いるマス」+1)を埋める
　　　キューに(行+1,列)を追加
(5)右マス(行,列+1)について
　・グリッドを飛び出していない(列+1<W)　かつ　壁でない　場合
　　・(右マスに書いている数)く(「今いるマス」+1)であれば
　　　右マスに(「今いるマス」+1)を埋める
　　　キューに(行,列+1)を追加
(6)(2)~(5)をキューが空になるまで繰り返す。

dequeについて
dequeはリストのようなものですが、先頭から要素を取り出す操作をO(1)で行うことができます。
(リストだとO(N)かかります)
import：from collections import deque
作成：変数名=deque()
末尾に要素追加【O(1)】：変数名.append(要素)
先頭から要素を取り出して削除【O(1)】：変数名.popleft()
【使用例】

# インポート
from collections import deque

# 作成：変数名=deque()
que=deque()

# 末尾に要素追加 O(1)：変数名.append(要素)
que.append(1)

# 先頭から要素を取り出して削除 O(1)：変数名.popleft()
x=que.popleft()

詳しく知りたい人は以下のページを見てください。

【提出】

# 入力の受け取り
H,W=map(int,input().split())

# グリッド
grid=[]

# i=0~(H-1)
for i in range(H):
    # 入力の受け取り
    tmp=input()
    # 一文字ずつリストへ
    tmp_list=list(tmp)
    # グリッドへ追加
    grid.append(tmp_list)

# そこに至るまでに通ったマスの数を記録
# 初期値は全部0
count=[[0]*W for i in range(H)]

# スタート地点=1
count[0][0]=1

# dequeをインポート
from collections import deque
que=deque()

# (1)キューに(0,0)(=スタート地点)を入れる
que.append([0,0])

# キューが空になるまで
while 0<len(que):
    # (2)キューから要素を取り出す(=「今いるマス」の(行,列))
    gyou,retu=que.popleft()
    # (3)「今いるマス」の数字を確認する
    now_count=count[gyou][retu]
    
    # (4)下マス(行+1,列)について
    # ・グリッドを飛び出していない(行+1<H)　かつ　壁でない　場合
    if gyou+1<H and grid[gyou+1][retu]==".":
        # ・(下マスに書いている数)く(「今いるマス」+1)であれば
        if count[gyou+1][retu]<now_count+1:
            # 下マスに(「今いるマス」+1)を埋める
            count[gyou+1][retu]=now_count+1
            # キューに(行+1,列)を追加
            que.append([gyou+1,retu])

    # (5)右マス(行,列+1)について
    # ・グリッドを飛び出していない(列+1<W)　かつ　壁でない　場合
    if retu+1<W and grid[gyou][retu+1]==".":
        # ・(右マスに書いている数)く(「今いるマス」+1)であれば
        if count[gyou][retu+1]<now_count+1:
            # 右マスに(「今いるマス」+1)を埋める
            count[gyou][retu+1]=now_count+1
            # キューに(行,列+1)を追加
            que.append([gyou,retu+1])

# 答え
ans=0

# 最大の数が書いているマスを探索
# gyou=0~(H-1)
for gyou in range(H):
    # retu=0~(W-1)
    for retu in range(W):
        # カウント数がansより大きければ更新
        ans=max(ans,count[gyou][retu])

# 答えを出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】