ABC230 A～E問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC230(AtCoder Beginner Contest 230)　A～E問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - AtCoder Quiz 3

Nが42未満ならばNを出力
Nが42以上ならば(N+1)を出力

とします。ただし先頭に0埋めを行う必要があります。

0埋めを行うには以下の3手順を踏みます。
(1)Nを文字列へ変換
str(数値)と書くことで変換できます。

(2)Nの桁数を確認
len(文字)と書くことで文字数を確認できます。この場合は文字数=桁数となります。

(3)桁数に応じた「0」を先頭へ追加
Nが1桁なら「00」、2桁なら「0」を先頭へ追加します。
文字列の結合は「+」を使います。「AGC」「00」「N(文字列)」を結合するなら
"AGC"+"00"+「N(文字列)」
となります。
「AGC」「00」は文字列なのでダブルクオーテーションをつけるのを忘れないようにしてください。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
N=int(input())

# Nが42未満ならば
if N<42:
    # Nを文字列へ変換
    N_str=str(N)
    # 桁数が1なら
    if len(N_str)==1:
        # 「AGC」+「00」+「N」を出力
        print("AGC"+"00"+N_str)
    # そうでなければ(桁数が2ならば)
    else:
        # 「AGC」+「0」+「N」を出力
        print("AGC"+"0"+N_str)
else:
    # (N+1)を文字列へ変換
    N_str=str(N+1)
    # 桁数が1なら
    if len(N_str)==1:
        # 「AGC」+「00」+「N」を出力
        print("AGC"+"00"+N_str)
    # そうでなければ(桁数が2ならば)
    else:
        # 「AGC」+「0」+「N」を出力
        print("AGC"+"0"+N_str)

B - Triple Metre

Tを実際に作って、1文字ずつ順番に確認しましょう。
「oxx」を10^5個結合した文字列Tは以下のように書きます。
T="oxx"*(10**5)

あとはTのi文字目～(i+(Sの文字数))文字目までが一致しているか確認します。
Tのa文字目～b文字目は
T[a:b+1]
と書きます。
※pythonでは先頭を0文字目、次を1文字目、...と数えることに注意してください

一致していたら「Yes」を出力して終了します。
途中で終了する場合は
exit()
と書きます。

【提出】

# 入力の受け取り
S=input()
# Sの文字数
N=len(S)

# Tを作る
T="oxx"*(10**5)

# i=0~((Tの長さ)-N-1)
for i in range(len(T)-N):
    # もしTのi文字目～(i+N-1)文字目がSと一致していたら
    if T[i:i+N]==S:
        # 「Yes」を出力
        print("Yes")
        # 終了
        exit()

# 「No」を出力
print("No")

C - X drawing

まずなにはともあれ紙とペンを用意します。
操作後にどこが塗られるか、具体的に描いてみましょう。

例として以下の入力を考えます。
N：5
A B：3 2
P Q：2 4
R S：2 5

1つ目の操作から考えます。
【kの条件】
max(1−A,1−B)≤k≤min(N−A,N−B)
これに数値をそのまま当てはめます。
max(1−3,1−2)≤k≤min(5−3,5−2)
⇔max(-2,-1)≤k≤min(2,3)
⇔-1≤k≤2
【黒く塗るマス】
(A+k,B+k)
(2,1)
(3,2)
(4,3)
(5,4)

2つ目の操作も同様に考えます。
【kの条件】
max(1−A,B−N)≤k≤min(N−A,B−1)
これに数値をそのまま当てはめます。
max(1−3,2-5)≤k≤min(5−3,2-1)
⇔max(-2,-3)≤k≤min(2,1)
⇔-2≤k≤1
【黒く塗るマス】
(A+k,B-k)
(1,4)
(2,3)
(3,2)
(4,1)

塗る箇所は以下のようになります。太い黒枠はP,R,R,Sで指定された範囲です。
本来黒で塗るのですが、わかりやすいように色を塗り分けています。
・1つ目の操作で塗ったマス=赤
・2つ目の操作で塗ったマス=青
・両方の操作で塗ったマス=紫

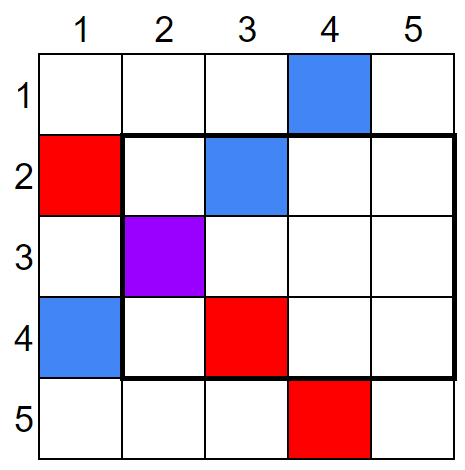
どうやら
1つ目の操作=左上→右下へ
2つ目の操作=右上→左下へ
マスを塗ることがわかります。

左上、右下、右上、左下のマスは簡単に計算できます。
1つ目の操作で得られるkの下限,上限をk1_left,k1_right
2つ目の操作で得られるkの下限,上限をk2_left,k2_right
とします。(kに関する不等式の左、右の意味です)

それぞれの行,列は以下のようになります。
左上：(A+k1_left,B+k1_left)
右下：(A+k1_right,B+k1_right)
右上：(A+k2_left,B-k2_left)
左下：(A+k2_right,B-k2_right)

あとはそれぞれのマスについて黒く塗られているか確認します。
・塗られている範囲内にあるマスか
　(行,列)がそれぞれ[左上]～[右下]の(行,列)範囲内または[右上]～[左下]の(行,列)範囲内にあるか確認します。
　具体的には(行,列)=(i,j)として以下が成り立つ必要があります。
　[左上]行≤i≤[右下]行 かつ [左上]列≤j≤[右下]列
　または
　[右上]行≤i≤[左下]行 かつ [左下]列≤j≤[右上]列

・塗られているマスか
　[左上]から斜め45度降りた場所にあるマス
　または
　[左下]から斜め45度上がった場所にあるマス
　であればよいです。
　具体的には(行,列)=(i,j)として以下が成り立つ必要があります。
　i-[左上]行=j-[左上列]
　または
　[左下]行-i=j-[左下]列

これらの条件を各マスについて確かめます。実装のときは変数名をx1,x2などではなく、[左上]=leftup,[右下]=rightlowなど何を表したものなのか明確にしておくとバグを起こしにくいです。

【提出】

# 入力の受け取り
N,A,B=map(int,input().split())
P,Q,R,S=map(int,input().split())

# 1つ目の操作：Kの下限
k1_left=max(1-A,1-B)
# 1つ目の操作：Kの上限
k1_right=min(N-A,N-B)

# 2つ目の操作：kの下限
k2_left=max(1-A,B-N)
# 2つ目の操作：kの上限
k2_right=min(N-A,B-1)

# 左上の(行,列)
leftup_gyou,leftup_retu=A+k1_left,B+k1_left
# 右下の(行,列)
rightlow_gyou,rightlow_retu=A+k1_right,B+k1_right
# 右上の(行,列)
rightup_gyou,rightup_retu=A+k2_left,B-k2_left
# 左下の(行,列)
leftlow_gyou,leftlow_retu=A+k2_right,B-k2_right

# 答え：最初は全てのマスが白
# 0インデックスのため「S-R+1」+1,「Q-P+1」+1とする
ans=[["."]*(S-R+1+1) for i in range(Q-P+1+1)]

# 行：i
for i in range(P,Q+1):
    # 列：j
    for j in range(R,S+1):
        # 左上～右下の範囲にあるかチェック
        if leftup_gyou<=i<=rightlow_gyou and leftup_retu<=j<=rightlow_retu:
            # 黒マスかどうかのチェック
            if i-leftup_gyou==j-leftup_retu:
                # 黒に塗る
                ans[i-P+1][j-R+1]="#"
        # 右上～左下の範囲にあるかチェック
        if rightup_gyou<=i<=leftlow_gyou and leftlow_retu<=j<=rightup_retu:
            # 黒マスかどうかのチェック
            if leftlow_gyou-i==j-leftlow_retu:
                # 黒に塗る
                ans[i-P+1][j-R+1]="#"

# 行=1~((Q-P+1+1)-1)まで
for gyou in range(1,Q-P+1+1):
    # gyou行目の情報
    ans_gyou=""
    # 列=1~((S-R+1+1)-1)まで
    for retu in range(1,S-R+1+1):
        # 一列ずつ黒か白か確認
        ans_gyou+=ans[gyou][retu]
    # 出力
    print(ans_gyou)

D - Destroyer Takahashi

「区間スケジューリング」と呼ばれる典型問題です。

まず壁の情報を右端の列番号が小さい順にソートします。
二次元配列のk番目の要素をもとにソートする場合は以下のように書きます。
(リスト).sort(key=lambda x:x[k])

壁を壊す時はソートした順に壁の右端へパンチしていきます。
このとき、次の壁の左端列番号が(パンチした場所＋D-1)より左にあれば、その壁はそれまでのパンチで壊れているので再度パンチする必要はありません。

なぜこの方法でうまくいくのかは公式解説で証明されているとおりですが、自分で図を書いて確かめるとより直感的に理解できるかもしれません。

【提出】

# 入力の受け取り
N,D=map(int,input().split())

# 区間の情報
section=[]

# N回
for i in range(N):
    # 入力の受け取り
    l,r=map(int,input().split())
    # 情報を格納
    section.append([l,r])

# 右端の列番号を基準にソート
section.sort(key=lambda x:x[1])

# 最初の壁の右端にパンチを打つ
punch=section[0][1]
# 答え
ans=1

# i=1~(N-1)
for i in range(1,N):
    # i番目の壁の左端、右端
    left,right=section[i][0],section[i][1]
    # 最後にパンチした壁+(D-1)<左端
    # ⇔最後のパンチでi番目の壁を壊せていなければ
    if punch+D-1<left:
        # 右端にパンチを打つ
        punch=right
        # 回数をカウント
        ans+=1

# 答えの出力
print(ans)

E - Fraction Floor Sum

まず[N/i]をi=1~Nまで計算してみましょう。
例としてN=100とすると以下のようになります。

100 50 33 25 20 16 14 12 11 10 9 8 7 7 6 6 5 5 5 5 4 4 4 4 4 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

当たり前ですが後ろの方は同じ数がいくつも並ぶことがわかります。
そこであるkについて
k=[N/i]
となるiがいくつあるのか考えてみます。
たとえばk=1ならばi=51~100で50個存在することがわかります。
k=2ならばi=34~50で17個です。
一般のkについてはi=([N/(k+1)]+1)~[N/k]までがk=[N/i]となるiです。
個数は([N/k]-[N/(k+1)])個となります。
よってk=1,2,...についてk*([N/k]-[N/(k+1)])を計算すれば値は出るのですが、kが取りうるのは1~Nなので全部試すとTLEします。

そこでk=1~√Nまでを上記方法で計算し、それ以外の場合は愚直に計算します。
[N/i]が√Nより大きくなるのはi=1~[N/([√N]+1)]の間です。これならO(√N)で計算できるので間に合います。

【提出】

# 入力の受け取り
N=int(input())

# 答え
ans=0

# [√N]を計算
from math import sqrt
N_sqrt=int(sqrt(N))

# [N/i]=kとなるもの
# k=1～[√N]まで
for k in range(1,N_sqrt+1):
    # kとなるものが([N/k]-[N/(k+1)])個
    ans+=k*(int(N/k)-int(N/(k+1)))

# [N/i]を計算
# i=1～([N/([√N]+1)])まで
for i in range(1,int(N/(N_sqrt+1))+1):
    # 答えの計算
    ans+=int(N/i)

# 答えを出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】