エイシングプログラミングコンテスト2021 A~D問題の解説記事です。
(AtCoder Beginner Contest 202)
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
AISing(エイシング)様について
このコンテストはAISing Ltd.(エイシング)様が主催されています。
エイシング様は、2016年に設立されたAIスタートアップです。
開発した独自のAIアルゴリズムであるAiiR(AI in Real-time)シリーズは、 Deep Learningのような従来のAIアルゴリズムでは難しいとされてきた、 エッジでの学習や調整のいらない逐次学習を可能とした事で、数多くのスタートアップアワードを受賞されています。
経済産業省の育成プログラムであるJ-Startupでは、日本のユニコーン企業(時価総額1,000億円以上の未上場企業)候補92社に選出されています。
興味がある方はホームページをご覧ください。
A - Three Dice
aの裏面は7-a
bの裏面は7-b
cの裏面は7-c
ゆえに答えは(7-a)+(7-b)+(7-c)=21-(a+b+c)です。
これを出力すればよいです。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出】
# 入力の受け取り
a,b,c=map(int, input().split())
# 21-(a+b+c)を出力
print(21-(a+b+c))
B - 180°
問題文のとおりに実装します。
すなわち以下を行います。
(1)Sを反転する
反転はS[::-1]と書くことでできます。
よく出てくる書き方ですが、「python 文字列 反転」等で検索すればすぐに出てくるのでわざわざ覚える必要はありません。
(2)変換する
Sの文字それぞれを順に処理するときは以下のように書きます。
for x in S:
こうすることでSを1文字ずつxへ格納して処理ができます。
あとはif文で各変換を行えばよいです。
0→0
1→1
6→9
8→8
9→6
【提出】
# 入力の受け取り
S=input()
# Sを反転
S=S[::-1]
# 答えを格納する変数
ans=""
# Sの文字をそれぞれxへ
for x in S:
# x=「0」ならば
if x=="0":
# 「0」を末尾へ追加
ans+="0"
# x=「1」ならば
elif x=="1":
# 「1」を末尾へ追加
ans+="1"
# x=「6」ならば
elif x=="6":
# 「9」を末尾へ追加
ans+="9"
# x=「8」ならば
elif x=="8":
# 「8」を末尾へ追加
ans+="8"
# x=「9」ならば
elif x=="9":
# 「6」を末尾へ追加
ans+="6"
# 答えを出力
print(ans)
C - Made Up
以下の入力を例に考えます。
N=5
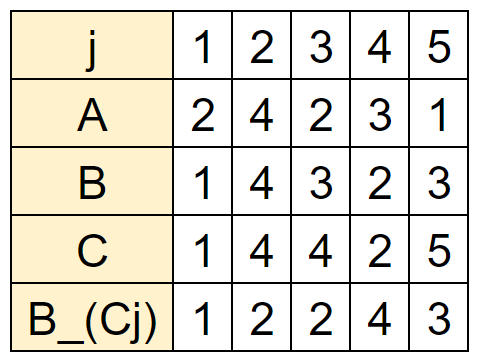
A:2 4 2 3 1
B:1 4 3 2 3
C:1 4 4 2 5
AとB_(Cj)の組を調べるので、まずB_(Cj)を考えましょう。
j=1~5まで代入して調べてみます。
j=1:B_(C1)=B_(1)=1
j=2:B_(C2)=B_(4)=2
j=3:B_(C3)=B_(4)=2
j=4:B_(C4)=B_(2)=4
j=5:B_(C5)=B_(5)=3
この表のAとB_(Cj)について値が同一になる組を確認します。
A[1]とB_(Cj)[1],B_(Cj)[2],...
A[2]とB_(Cj)[1],B_(Cj)[2],...
と順に確認していくと計算量がO(N^2)となるのでTLEします。
まずAとB_(Cj)に1~N(=5)がいくつ含まれるか確認しましょう。
1:A→1個 B_(Cj)→1個
2:A→2個 B_(Cj)→2個
3:A→1個 B_(Cj)→1個
4:A→1個 B_(Cj)→1個
5:A→0個 B_(Cj)→0個
1についてはAに1個、Bに1個ですから、作れる組み合わせは1個です。
組:(A[5],B_(Cj)[1])
これは(Aに1が含まれる個数)×(B_(Cj)に1が含まれる個数)=1×1で計算できます。
2についてはAに2個、Bに2個ですから、作れる組み合わせは4個です。
組:(A[1],B_(Cj)[2]) , (A[1],B_(Cj)[3]) , (A[3],B_(Cj)[2]) , (A[3],B_(Cj)[3])
これは(Aに2が含まれる個数)×(B_(Cj)に2が含まれる個数)=2×2で計算できます。
同様にして考えると
3については1×1=1
4については1×1=1
5については0×0=0
よって合計は1+4+1+1+0=7で7組です。
この方法なら事前に1~N(=5)がいくつ含まれるか計算しておけばO(N)で終わるためTLEしません。
実装では
Aの値をカウントするリスト=A_count
B_Cjの値をカウントするリスト=B_Cj_count
を作り、for文で値を確認していきます。
(例:A_count[2]=3だったらAに「2」が3個ある)
この問題は1インデックスで受け取るため、入力時にA[0],B[0],C[0]を0で埋めています。
インデックス番号をずらして入力と合わせるためで、0という数字に特に意味はありません。
【提出】
# 入力の受け取り
N=int(input())
# 0番目を埋めるため[0]とする
A=[0]+list(map(int, input().split()))
B=[0]+list(map(int, input().split()))
C=[0]+list(map(int, input().split()))
# B_(Cj)の値を格納するリスト
B_Cj=[0]*(N+1)
# j=1~Nまで
for j in range(1,N+1):
# B_(Cj)の値を確認
B_Cj[j]=B[C[j]]
# Aの値をカウントするリスト
# 例:A_count[2]=3だったらAに「2」が3個ある
A_count=[0]*(N+1)
# i=1~Nまで
for i in range(1,N+1):
# Aの値を確認し、カウントしていく
A_count[A[i]]+=1
# B_Cjの値をカウントするリスト
B_Cj_count=[0]*(N+1)
# i=1~Nまで
for i in range(1,N+1):
# B_Cjの値を確認し、カウントしていく
B_Cj_count[B_Cj[i]]+=1
# 答えを格納する変数
ans=0
# i=1~Nまで
for i in range(1,N+1):
# (Aにiが含まれる個数)×(B_(Cj)に2が含まれる個数)
ans+=A_count[i]*B_Cj_count[i]
# 答えの出力
print(ans)
D - aab aba baa
以下の入力を例に考えましょう。
A(「a」の個数):2
B(「b」の個数):2
K:5
「a」2文字、「b」2文字を並び替えて辞書順5番目のものを探します。
・1文字目(確定:「○○○○」)
まず1文字目が「a」か「b」か考えましょう。
『「a○○○」のうち辞書順最初のもの』は当然1番目です。
(具体的には「aabb」です)
『「b○○○」のうち辞書順最初のもの』は何番目でしょうか。
これは『「a○○○」の数』がいくつあるか確認すれば計算できます。
なぜなら『「b○○○」のうち辞書順最初のもの』は「a○○○」のものが全て出尽くした次の文字列だからです。
「a○○○」がいくつあるかは○○○の順列の数を数えればわかります。
「a○○○」は「a」を先頭に1個使っているので○○○の部分に「a」1個、「b」2個が入ります。
同じものを含む順列なので
(aの個数+bの個数)C(bの個数)
=(1+2)C2
=3C2=3
と数えることができます。
具体的には「aabb」「abab」「abba」の3通りです。
※同じものを含む順列がよくわからない人は以下のページを見てください。
『「b○○○」のうち辞書順最初のもの』はこの3つの直後にでてくるわけですから、
『「b○○○」のうち辞書順最初のもの』は辞書順何番目か
=『「a○○○」のうち辞書順最初のもの』+『「a○○○」の数』
=1+3=4番目
であることがわかります。
『「a○○○」のうち辞書順最初のもの』=1番目
『「b○○○」のうち辞書順最初のもの』=4番目
で、K=5は4以上ですから、最初の文字は「b」であり、答えは少なくとも「b○○○」であることがわかります。
・2文字目(確定:「b○○○」)
次に「ba○○」なのか「bb○○」なのか考えます。すなわち2番目の文字を確定させます。
『「ba○○」のうち辞書順最初のもの』は『「b○○○」のうち辞書順最初のもの』と一致します。計算したとおり4番目です。
『「bb○○」のうち辞書順最初のもの』は『「ba○○」の数』がいくつあるか確認すれば計算できます。
「ba○○」がいくつあるかは○○の順列の数を数えればわかります。
「ba○○」は「a」,「b」を先頭に1個ずつ使っているので残り「a」1個、「b」1個が入ります。
1文字目同様に
(aの個数+bの個数)C(bの個数)
=(1+1)C1
=2C1=2
と数えることができます。
具体的には「baab」「baba」の2通りです。
『「bb○○」のうち辞書順最初のもの』はこの2つの直後にでてくるわけですから、
『「bb○○」のうち辞書順最初のもの』は辞書順何番目か
=『「ba○○」のうち辞書順最初のもの』+『「ba○○」の数』
=4+2=6番目
であることがわかります。
『「ba○○」のうち辞書順最初のもの』=4番目
『「bb○○」のうち辞書順最初のもの』=6番目
で、K=5は6より小さいですから、2番目の文字は「a」であり、答えは少なくとも「ba○○」であることがわかります。
・3文字目(確定:「ba○○」)
次に「baa○」なのか「bab○」なのか考えます。すなわち3番目の文字を確定させます。
『「baa○」のうち辞書順最初のもの』は『「ba○○」のうち辞書順最初のもの』と一致します。計算したとおり4番目です。
『「bab○」のうち辞書順最初のもの』は『「baa○」の数』がいくつあるか確認すれば計算できます。
「baa○」は計算しなくても明らかに「baab」の1通りしか作れないことはわかりますが、無理やりnCrを使うと
(aの個数+bの個数)C(bの個数)
=(0+1)C1
=1C1=1
と計算できます。
『「bab○」のうち辞書順最初のもの』は同じように計算して
『「bab○」のうち辞書順最初のもの』は辞書順何番目か
=『「baa○」のうち辞書順最初のもの』+『「baa○」の数』
=4+1=5番目
であることがわかります。
『「baa○」のうち辞書順最初のもの』=4番目
『「bab○」のうち辞書順最初のもの』=5番目
で、K=5は5以上ですから、3番目の文字は「b」であり、答えは少なくとも「bab○」であることがわかります。
・4文字目(確定:「bab○」)
最後に4文字目を確定させますがこれは簡単です。
使える文字がもう「a」しか残っていないからです。4文字目は「a」を使うしかありません。
「baba」となります。
よって答えは「baba」となります。
以上のように先頭の文字から順に確定させていきます。
実装は以下のように行います。
○確定した文字のうち辞書順最初のものが何番目か記録する変数(=num)を作る
初期値は1
(1)「a」の残り個数(=A)または「b」の残り個数(=B)が0ならば残っている文字を末尾へつけるを繰り返す
(2)『確定していない部分の最初の文字が「b」の辞書順最初の文字』が何番目か(=b_start)計算する
→num+『確定していない部分の最初の文字が「a」である場合の順列の数』
→num+『「a」が(A-1)個、「b」がB個の順列の数』
→num+(A-1+B)CB
(3)Kとb_startを比較する
・もしKがb_startより小さいならば(確定していない部分の最初の文字は「a」)
「a」を末尾へ追加
「a」を使ったのでAをマイナス1
・そうでないなら(Kがb_start以上、確定していない部分の最初の文字は「b」)
「b」を末尾へ追加
「b」を使ったのでBをマイナス1
(4)(1)~(3)をA,Bが0になるまで繰り返す。
nCrの計算は関数で用意しておきます。
nCr=n!/(r!(n-r)!)を計算すればよいです。
階乗はmathのfactorialで計算できます。
【提出】
# 階乗
from math import factorial
# nCr 引数:n,r→戻り値:nCr
def nCr(n,r):
# 分子
numerator=factorial(n)
# 分母
denominator=factorial(n-r)*factorial(r)
# (分子)/(分母)を返す
return numerator//denominator
# 入力の受け取り
A,B,K=map(int, input().split())
# 答えを格納する変数
ans=""
# 確定した文字列が辞書順何番目か
num=1
# A(「a」の残り個数)かB(「b」の残り個数)が0より大きい間
while 0<A or 0<B:
# もしAが0ならば
if A==0:
# 「b」を末尾へ
ans+="b"
# 「b」の数を1個減らす
B-=1
# 繰り返し
continue
# もしBが0ならば
if B==0:
# 「a」を末尾へ
ans+="a"
# 「a」の数を減らす
A-=1
# 繰り返し
continue
# 『確定していない部分の最初の文字が「b」』の辞書順最初の文字が何番目か
# num+『確定していない部分の最初の文字が「a」である場合の順列の数』
# num+『「a」が(A-1)個、「b」がB個の順列の数』
b_start=num+nCr(A-1+B,B)
# もしKがb_startより小さいならば
if K<b_start:
# 末尾に「a」を追加
ans+="a"
# 「a」の数を1個減らす
A-=1
# そうでないなら(もしb_start<=Kならば)
else:
# 末尾に「b」を追加
ans+="b"
# 辞書順で(b_start)番目
num=b_start
# 「b」の数を1個減らす
B-=1
# 答えの出力
print(ans)
【広告】
『AtCoder 凡人が『緑』になるための精選50問詳細解説』
AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段:100円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
1~24問目まではサンプルとして無料公開しています
『AtCoder ABC201~225 ARC119~128 灰・茶・緑問題 超詳細解説』
ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを5問分公開しています
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
ARC119~128の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
【booth(pdf)】
『Excelでリバーシを作ろう!! マクロ、VBAを1から学ぶ』
Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です!
マクロ、VBAが全くわからない人でも大丈夫! 丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます!
値段:300円(Kindle Unlimited対象)
サンプルとして「準備」~「三目並べ」を無料公開しています。
【kindle】
【booth(pdf】