ABC208 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC208(AtCoder Beginner Contest 208)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Rolling Dice

A回全て1が出た場合、出た目の合計はA
A回全て6が出た場合、出た目の合計は6A
となりますから、
A≤B≤6A　ならば　Yes
そうでないならば　No
を出力します。

Yes、Noは文字列なので
print("Yes")
というように""をつけることを忘れないようにしてください。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
A,B=map(int, input().split())

# A<=B<=6Aの時
if A<=B<=6*A:
    # Yesを出力
    print("Yes")
# そうでない時
else:
    # Noを出力
    print("No")

B - Factorial Yen Coin

単純に額の大きなコインから使っていけばよいです。
10!≤P!なら10!コインを使う(Pから10!を引く)
P<10!になったら次は9!コインを使う
...
をPが0になるまで繰り返します。

階乗については標準ライブラリ math に factorial という関数があるのでそれを使います。
まず import math を書きましょう。
xの階乗はmath.factorial(x)と書くことで計算できます。

for文について10~1のように大きい数から小さい数へ処理したいときは
for i in range(スタート,ストップ-1,一回ごとに減らす量)
と書きます。

10~1の場合は
スタート：10
ストップ：1
減らす量：-1
となりますから
for i in range(10,0,-1):
と書けばOKです。

【提出】

# 入力の受け取り
P=int(input())

# 答えを格納する変数
ans=0
# mathのインポート
import math

# i=10～0まで、-1ずつ
for i in range(10,0,-1):
    # i!円のコイン
    coin=math.factorial(i)

    # コインよりPが大きい間
    while coin<=P:
        # コインを使う
        ans+=1
        # 使った分をマイナス
        P-=coin
        
# 答えを出力
print(ans)

C - Fair Candy Distribution

(K÷Nの商)個数は全員にお菓子が配られ、国民番号が小さい方から(K÷Nの余り)番目の人は+1個受け取れることがわかります。

例として以下の入力を考えましょう。
「入力例」
4 22
10 30 20 40

22÷4=5 余り 2
ですから、全員5個のお菓子はもらえることがわかります。
余り2個については国民番号の小さい順から2人がプラス1個もらえます。

そこで国民番号(number)が小さい順から何番目なのか(order)変換する連想配列を作りましょう。
※連想配列がわからない人は以下のサイトを参考にしてください。

まず国民番号を小さい順にソートします。
この時A自体をソートするのではなく、A_sortという別の変数へソートしたAを記録します。
A_sort：10 20 30 40

そして小さい順に1,2,3...と連想配列(number_order)で記録します。
number_order[10]=1
number_order[20]=2
number_order[30]=3
number_order[40]=4

このように　数列の要素→小さい順から何番目　と変換する方法を
座標圧縮
と呼びます。

あとはAの要素(国民番号)それぞれについて何番目なのかを変換して確認し、
(余り)番目以下の人：(商)+1個のお菓子
(余り)番目より大きい人：(商)個のお菓子
と出力すればOKです。

【提出】

# 入力の受け取り
N,K=map(int, input().split())
A=list(map(int, input().split()))

# Aをソートした数列
A_sort=sorted(A)

# 国民番号→順序への変換
number_order=dict()

# i=0~Nまで
for i in range(N):
    # 国民番号→順序への変換
    number_order[A_sort[i]]=i+1

# K÷Nの商
syou=K//N
# K÷Nの余り
amari=K%N

# Aのそれぞれの要素について
for num in A:
    # 順序が余り以下なら
    if number_order[num]<=amari:
        # 商+1を出力
        print(syou+1)
    # そうでないなら(順序が余りより大きいなら)
    else:
        # 商を出力
        print(syou)

D - Shortest Path Queries 2

ワーシャルフロイド法を使います。
ワーシャルフロイド法は重み付き有向グラフの全ペアの最短経路問題を、頂点の数をNとしてO(N^3)で解くアルゴリズムです。
要するに一方通行の道路が各都市間に敷いてある時、ある都市から他の都市まで一番速くて何分で着くかを計算できるアルゴリズムです。

例として以下の入力を考えましょう。
「入力例」
4 4
2 1 1
1 3 2
3 4 2
1 4 5

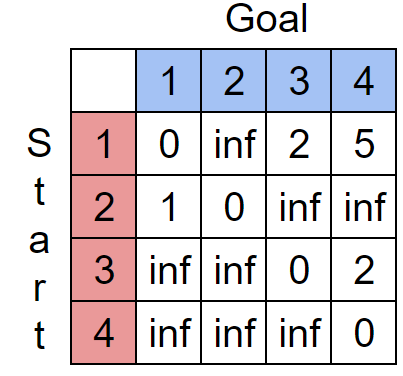
まず都市間の移動時間を表にします。以下のようになります。

StartからGoalまで何分かかるかを表した表です。
(例えば都市2→都市1は Start：2 Goal：1 を見て「1分」とわかります)
StartとGoalが同じ場合は0分です。
infはinfinity(無限大)分、すなわち到達不可能であることを表します。

次にk=1、すなわち都市1のみ通って良い場合、各都市間の移動時間を考えましょう。
これは各Start、Goalについて、
・直接向かう場合　Start→Goal
・都市1を経由する場合　Start→都市1→Goal
どちらか小さい方を採用します。

たとえば都市2から都市3について、上記の表を確認しながら計算しましょう。
・直接向かう場合　都市2→都市3：inf
・都市1を経由する場合　都市2→都市1 + 都市1→都市3：1+2=3
3<infなので、都市1を経由する場合のほうが早く着きます。

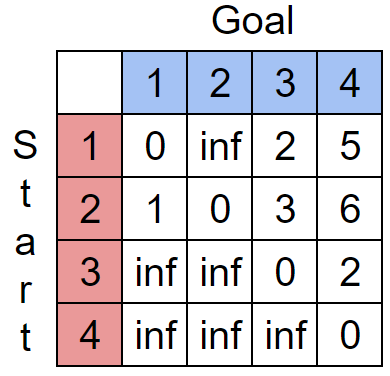
各都市について、同様に計算し、表を埋めると以下のようになります。

K=1(都市番号が1以下の都市のみ通った場合の最短時間)

この表はs=Start,t=Goalとしたときのf(s,t,1)を表しています。
例えばf(2,4,1)=6ということが表を見るだけでわかります。

ゆえに表のinf以外の箇所を全て足せば
Σ[s=1,N]Σ[t=1,N]f(s,t,1)
すなわちk=1のとき、任意のs,tの組についてfを合計したものを計算することができます。

次にk=2、すなわち都市番号が2以下の都市のみ通って良い場合、各都市間の移動時間を考えましょう。

すでにK=1(都市番号が1以下の都市のみ通った場合の最短時間)の各都市間時間は表にしました。
この表を使い、同じ手順で今度は都市2を経由する場合を考えればよいです。
つまり各Start、Goalについて、
・直接向かう場合　Start→Goal
・都市2を経由する場合　Start→都市2→Goal
これらを「K=1」の表を見ながら計算し、どちらか小さい方を採用します。
「K=1」の表を見て計算することで「都市番号2以下」の都市のみ使用した場合の最短時間を計算できるというわけです。

表が埋まったらまたinf以外の全ての箇所を足し算して
Σ[s=1,N]Σ[t=1,N]f(s,t,2)
すなわちk=2のとき、任意のs,tの組についてfを合計したものを計算することができます。

あとはこれをひたすら繰り返すだけです。
参考までにk=4まで埋めた表は以下のようになります。

K=4(都市番号が4以下の都市のみ通った場合(全ての都市を通行可能)の最短時間)

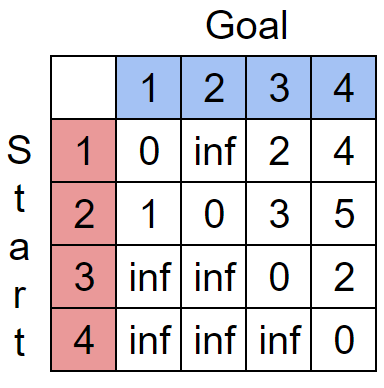
この表は任意の都市間の最短到達時間を示しています。
このようにN^3回の計算で最短到達時間を計算できるのがワーシャルフロイド法です。

実装では
(1)入力を受け取って表を作る(time)
(2)k=1,2,3...について新しい表(new_time)を作り、
・直接向かう場合　Start→Goal
・都市kを経由する場合　Start→都市k→Goal
を表(time)を見ながら計算し、どちらか小さい方を新しい表(new_time)に埋める
(3)new_timeのinfでない部分を全て足し算
(4)timeをnew_timeへ置き換える
(5)次のkについて(2)～(4)を行う
として最後に計算結果を出力すればOKです。

【infについて】
実装では
inf=10**10
など大きな数を用意しますが、大きすぎる(10^20等)とTLEします

pythonでは間に合わないため、pypyで提出します。

【提出】

# pypyで提出

# 入力の受け取り
N,M=map(int, input().split())

# 到達不可能時間(バカでかい数ならなんでも)
inf=10**10
# 時間表
time=[[inf]*(N+1) for i in range(N+1)]

# i=1~Nまで
for i in range(1,N+1):
    # 1→1、2→2、...を時間0へ
    time[i][i]=0

# M回
for i in range(M):
    # 入力の受け取り
    A,B,C=map(int, input().split())
    # 時間表の更新
    time[A][B]=C

# 答えを格納する変数
ans=0

# k=1~N
for k in range(1,N+1):
    # 新しい時間表
    new_time=[[0]*(N+1) for i in range(N+1)]

    # スタート都市　1~N
    for start in range(1,N+1):
        # ゴール都市　1~N
        for goal in range(1,N+1):
            # 新しい時間表を更新　古い時間表の時間　と　kを経由したときの時間　の小さい方
            new_time[start][goal]=min(time[start][goal],time[start][k]+time[k][goal])

            # 新しい時間表でスタート→ゴールが到達不能でなければ
            if new_time[start][goal]!=inf:
                # 新しい時間を答えにプラス
                ans+=new_time[start][goal]

    # 古い時間表を新しい時間表へ更新
    time=new_time

# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】