Juliaで学ぶ確率変数(2) - ２項分布（離散型）

Juliaで学ぶ確率変数(1) - 確率変数の定義 - Qiita
Juliaで学ぶ確率変数(11) - まとめ - Qiita

　確率変数を勉強中ですが、**「確率統計」（森北出版）は数学的に明確な定義がしっかり書かれているので、これを中心に勉強しています。あわせて「統計学入門」（東京大学出版会）と「確率論入門」（ちくま学芸文庫、赤攝也）**も併読しています。

　本記事は、それらの教科書を読みながら、実際に例題や問題をJuliaで解いていく試みです。Juliaの離散型確率変数のライブラリのドキュメントです。　==>Distributions/Univariate/DiscreteDistributions

#１．離散型確率変数の例

離散型確率変数は確率密度関数を具体的に与えることで定義されます。

以下に代表的な離散型確率変数の例を見ていくとともに、対応するJuliaの関数を使い、例題を計算したり、プロットしたりしていきたいと思います。

Distributionsには、代表的な分布の**確率密度関数（確率関数）**が揃っています。
以下はその例です。

2点分布の確率密度関数
Distributions.Bernoulli

2項分布の確率密度関数
Distributions.Binomial

幾何分布の確率密度関数
Distributions.Geometric

ポアソン分布の確率密度関数
Distributions.Poisson

***確率密度関数の評価関数
Distributions.pdf
Evaluate the probability density (mass) at x.

以上に挙げた確率密度関数は、実際には確率密度関数を定義するだけのものです。実際に定義された確率密度関数を実行（評価）するにはpdf関数 (Probability density function) を用います。

#２．２項分布 B(k;n,p)

ある試行をn回繰り返したとき、ある事象Aの起こる回数Xの確率分布を二項分布といいます。

２項分布 B(n;p)の確率密度関数の定義です。

一般的に、標本空間（全事象）や確率変数は必ずしも明示的に定義はされていない場合でも、確率密度関数（確率分布）だけ明示的に与えられ、問題を解く場合があります。「確率論入門」（ちくま学芸文庫、赤攝也）を除いて、他の教科書では、例題や問題において標本空間（全事象）や確率変数が明示的に示されることはほとんどないんですよね。しかも確率密度関数（確率分布）の定義においても明示されない場合があります。

「確率論入門」（ちくま学芸文庫、赤攝也）では、２項分布の説明にあたり、標本空間（全事象）や確率変数Xが、多重試行の確率変数として、明示的に定義されています。以下にまとめてみました。

\begin{align}
&\Omega:標本空間、　E:事象\\
&X_i^{(n)} : \Omega^{(n)} \rightarrow  \{0,1\}\\

&X_i^{(n)}(a_1,a_2,...,a_n) = 
\left\{
\begin{array}{ll}
1 & (a_i \in E) \\
0 & (a_i \notin E)
\end{array}
\right.\\
\\

&S^{(n)} : \Omega^{(n)} \rightarrow \{0,1,...,n\}\\
&S^{(n)} = X_1^{(n)} + X_2^{(n)} +...+ X_n^{(n)}\\
\\
&つまり、S^{(n)}(a_1,a_2,...,a_n) = k \;は以下のことを意味する。\\
&a_1,a_2,...,a_nのうちEに属するものの個数がk個である。\\
\\
&p \equiv p(E) \; とおくと、0 < p < 1、となる。\\
&確率変数S^{(n)}の確率密度関数は以下のようになる（反復試行の確率の定理）。\\
&f(k) = B(k;n,p) = \begin{pmatrix} n \\k \end{pmatrix} p^k (1-p)^{n-k} \qquad (k=0,1,...,n)\\
\\
&*** ２項定理より、\sum_{k=0}^n f(k) =1
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad \qquad  \qquad\\
\end{align}

２項分布B(n;p)の平均と分散を示しておきます。

\begin{align}
\\
&平均\\
&E[X] = np\\
\\
&分散\\
&V[X] = np(1-p)\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad\\
\end{align}

##２－１．２項分布を当たりくじで表現すると

確率密度関数f(k)は、当たる確率がPのくじをn本引いたときに、
ちょうどk本が当たる確率を意味する。

##２－２．Juliaで例題を解いてみる(1)

Juliaで分布を扱うための基礎知識は以下のページを参照してください。
「Juliaで学ぶ確率変数(1) - 確率変数の定義」の「４．Juliaで確率分布を扱う」

Juliaでは Distributions.Binomialを使います。

　前にも紹介しましたが、「確率論入門」（ちくま学芸文庫、赤攝也）の例題を計算してみます。以下の問題を考えます。

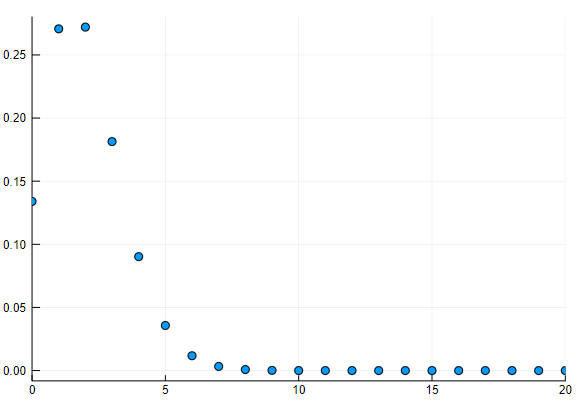
左利きの人が1%いる集団から1人選び、右利きか左利きかをみる。それを200回繰り返したときに4人以上が左利きである確率を計算する。

確率pの試行をn回繰り返す。ちょうどk回だけ成功する確率は以下の通り。
$$f(k)=p^k (1-p)^{n-k} * (n個からk個を取り出す組み合わせ数) \qquad　 \qquad$$

ちょうど4人が左利きである確率は以下の通りです。
$$f(x)=(1/100)^4 (1-(1/100))^{200-4} * (200から4を取り出す組み合わせ数)$$

この場合、**標本空間（全事象）や確率変数は必ずしも明示的に定義はされていないけど、確率密度関数は明示的に定義することができます。B(k;n,p)のk,n,pだけわかればよいわけです。**そして現実の問題を解くことができます。

　この問題を、Distributions.Binomialで解いてみます。big関数を使って精度を高め、計算がオーバーフローしないようにしています。

using Distributions
using StatPlots

d= Binomial(big(200), big(1/100))
println(cdf(d,200)-cdf(d,3))
scatter(d, leg=false, xlims = (0,20))
0.1419659655552563

d=Distributions.Binomialは確率密度関数の定義だけを返し、cdf(d,k)が、kを指定して、確率分布（kまでの累積）を計算します。cdf(d,200)-cdf(d,3)がK=4～200までの値になります。

##２－３．Juliaで例題を解いてみる(2)

ある工場で製造される工業製品には、0.1%の割合で不良品が混ざる。この工業製品1万個の中の不良品の個数をXであらわす。1万個の製品は独立に製造されたと考えるとき、Xの平均と分散を求めよ。

Xは2項分布 B(10000, 0.001) に従う。

using Statistics, Distributions
using StatPlots

n=10000
p=0.001
d= Binomial(n, p)

println("平均=", n*p)                 # 自力で計算
println("平均=", Statistics.mean(d))  # 平均関数で計算
println("分散=", n*p*(1-p))           # 自力で計算
println("分散=", Statistics.var(d))   # 分散関数で計算

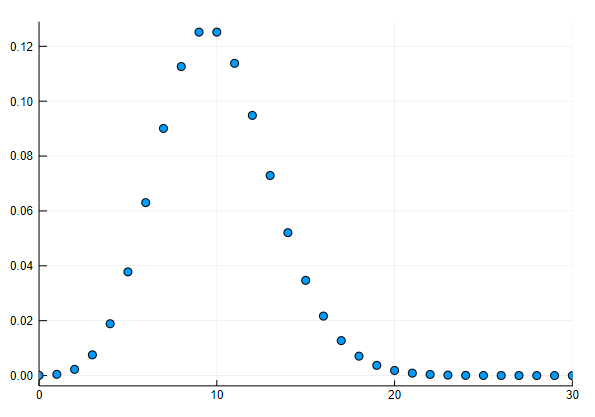
scatter(d, leg=false, xlims = (0,30)) # 0-30個までの散布図

当然ですが、平均値と分散は、自力の計算とStatisticsの関数で計算した値は等しいです。

出力結果

平均=10.0
平均=10.0
分散=9.99
分散=9.99

0-25までの確率密度関数の値を出力します。
（注意）Juliaではf.(A)という構文で配列Aの要素ごとに関数fを適用することができます。pdfでなくpdf.となっていることに注意してください。

pdf.(d,0:1:25)

出力結果

 4.517334597704865e-5  
 0.00045218564541590217
 0.0022629650993561605 
 0.007549257612066367  
 0.01888636845541227   
 0.037795423239299526  
 0.06302389977924569   
 0.09007019224850303   
 0.11262155044285409   
 0.12516010811088846   
 0.12517263665023892   
 0.11379330604567171   
 0.09481826277028821   
 0.07292252318084523   
 0.05207187466088258   
 0.03470068337427908   
 0.02167707229055156   
 0.012743560604655679  
 0.007074795101561427  
 0.00372059452630453   
 0.0018586213196719417 
 0.000884171827557367  
 0.0004014537568111273 
 0.0001743354478592268 
 7.254524371419332e-5  
 2.897743148319481e-5  

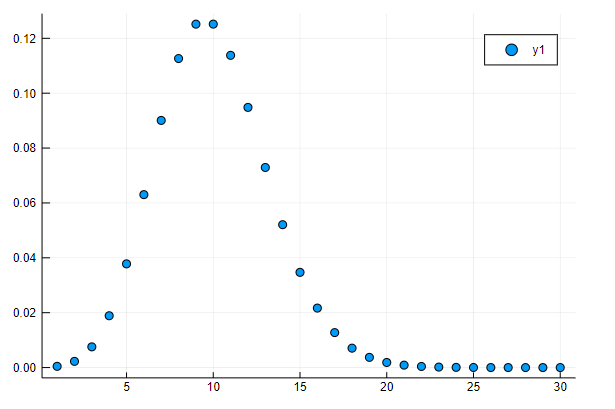
散布図はscatterでなく以下のようにplotでも描けますが、scatterの方が自然ですね。

plot(1:30, pdf.(d,1:30), seriestype=:scatter)

Juliaは素晴らしいツールですね。

今回は以上になります。