Juliaで学ぶ確率変数(1) - 確率変数の定義 - Qiita
Juliaで学ぶ確率変数(11) - まとめ - Qiita
確率変数を勉強中ですが、**「確率統計」(森北出版)は数学的に明確な定義がしっかり書かれているので、これを中心に勉強しています。あわせて「統計学入門」(東京大学出版会)と「確率論入門」(ちくま学芸文庫、赤攝也)**も併読しています。
本記事は、それらの教科書を読みながら、実際に例題や問題をJuliaで解いていく試みです。Juliaの連続型確率変数のライブラリのドキュメントです。 ==>Distributions/Univariate/ContinuousDistributions
1.一様分布 U(a,b)
\begin{align}
\\
\\
&a,bをa<bとなる定数とする\\
\\
&X: \Omega \rightarrow 区間 \; [a, b]\\
\\
&確率密度関数f(x)が以下のように書けるとき、Xは一様分布U(a,b)に従うという。\\
\\
&f(x) =
\left\{
\begin{array}{ll}
\frac{1}{b-a} & (a \leqq x \leqq b \;のとき) \\
0 & (x<a\;または\;b<xのとき)
\end{array}
\right.\\
\\
\\
&ここで、以下が成り立つ。\\
&E[X] = \int_{-\infty}^{\infty} xf(x) dx =\frac{a+b}{2}\\
&V[X] = \int_{-\infty}^{\infty} (x - E[X])^2 f(x) dx = \frac{(b-a)^2}{12}\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-1.Juliaで例題を解いてみる
Juliaで分布を扱うための基礎知識は以下のページを参照してください。
「Juliaで学ぶ確率変数(1) - 確率変数の定義」の「4.Juliaで確率分布を扱う」
Juliaでは正規分布の確率密度の定義はDistributions.Uniformを使います
サイト「連続一様分布2 - 統計Web」の例題をJuliaで解いてみましょう。
0以上5以下の範囲で乱数を10,000個作成したとき、その中で1以上2以下の値をとる確率はいくらでしょうか。
連続型確率変数の、区間[a,b]の確率は分布関数の引き算**cdf(d,b)-cdf(d,a)**で求まります。
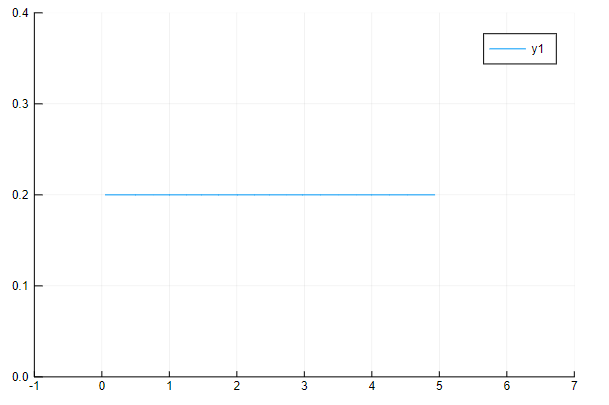
using Plots
using Distributions
using StatPlots
d=Uniform(0,5)
println( cdf(d,2)-cdf(d,1) )
plot(d,xticks = -1:1:7, xlims = (-1,7), ylims = (0,2/5))
cdf(d,2)-cdf(d,1)=0.2が出力されます。
今回は以上です。