Juliaで学ぶ確率変数(1) - 確率変数の定義 - Qiita
Juliaで学ぶ確率変数(11) - まとめ - Qiita
確率変数を勉強中ですが、**「確率統計」(森北出版)は数学的に明確な定義がしっかり書かれているので、これを中心に勉強しています。あわせて「統計学入門」(東京大学出版会)と「確率論入門」(ちくま学芸文庫、赤攝也)**も併読しています。
本記事は、それらの教科書を読みながら、実際に例題や問題をJuliaで解いていく試みです。Juliaの連続型確率変数のライブラリのドキュメントです。 ==>Distributions/Univariate/ContinuousDistributions
1.ガンマ分布G(α,ν)
ガンマ分布G(α,ν)のは、指数分布を一般化したもので、その持つ意味合いは、**期間1/αあたりに1回起こると期待されるランダムな事象がν回起こるまでの時間の分布、**と言われています。やはり製品部品の寿命やウイルスの潜伏期間のほか、人の体重なんかも従うらしいです。
\begin{align}
\\
\\
&定数 \alpha,\; \nu を\alpha>0,\; \nu>0 とする。\\
\\
&X: \Omega \rightarrow 非負の実数値\\
\\
&確率密度関数f(x)が以下のように書けるとき、Xはガンマ分布G(\alpha,\nu)に従うという。\\
\\
&f(x) =
\left\{
\begin{array}{ll}
\frac{1}{\Gamma (\nu)} \alpha^\nu x^{\nu-1} e^{-\alpha x} & (x \geqq 0 \;のとき) \\
0 & (x<0\;のとき)
\end{array}
\right.\\
\\
\\
&念のため x \geqq 0の時の定義を大きく書いておきます。\\
&f(x) = \frac{1}{\Gamma (\nu)} \alpha^\nu x^{\nu-1} e^{-\alpha x}
\\
\\
&ここで\Gamma (\nu)は解析学でガンマ関数と呼ばれるものです。\\
\\
\\
&ここで以下が成り立つ。\\
&E[X] = \frac{\nu}{\alpha}\\
&V[X] = \frac{\nu}{\alpha^2}\\
&p(\Omega)=\int_{-\infty}^{\infty} f(x) dx = \int_{0}^{\infty} \frac{1}{\Gamma (\nu)} \alpha^\nu x^{\nu-1} e^{-\alpha x} dx = 1\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-1.ガンマ関数の定義
\begin{align}
\\
&ガンマ関数の定義\\
&x>0の時\\
&\Gamma(x) =\int_{0}^{\infty} t^{x-1}e^{-t} dt\\
\\
\\
&ガンマ関数の性質\\
&[G1] \; \Gamma(1) = 1\\
\\
&[G2] \; \Gamma(x+1) = x\Gamma(x) \qquad 任意の実数x \geqq 1\\
&\qquad とくに、\\
&\qquad \Gamma(n+1) = n! \qquad 任意の非負整数n\\
\\
&[G3] \; \Gamma = \sqrt {\pi}\\
\\
\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
簡単なので[G2]の証明を見てみたいと思います。
\begin{align}
\\
&部分積分を使います。\\
&[G2] \; \Gamma(x+1) = \int_{0}^{\infty} t^{x} e^{-t} dt\\
&\qquad = \int_{0}^{\infty} t^{x} \frac {d \;(-e^{-t})}{dt} dt\\
&\qquad = [t^x(-e^{-t})]_0^\infty - \int_{0}^{\infty} \frac{d\;t^{x}}{dt} (-e^{-t}) dt\\
&\qquad =[-t^xe^{-t}]_0^\infty + \int_{0}^{\infty} xt^{x-1} e^{-t} dt\\
&\qquad = 0 + x \Gamma(x) = x \Gamma(x) \qquad \qquad Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-2.Juliaで解く例題
Juliaで分布を扱うための基礎知識は以下のページを参照してください。
「Juliaで学ぶ確率変数(1) - 確率変数の定義」の「4.Juliaで確率分布を扱う」
エクセルを用いたガンマ分布の計算の問題です。
--- 問題 ---
単位時間にα人の訪問者があるウェブの場合、ν人が訪問するまでの時間は次式の確率密度関数であるガンマ分布G(α,ν)に従う。訪問者が1分間に5人来るウェブの場合、訪問者が100人になる時間の確立密度分布を求めなさい。
--- Juliaの計算 ---
期間1/αあたりに1回起こると期待されるランダムな事象がν回起こるまでの時間の分布。
今の場合、問題より、1/α = 1/5です。
Juliaでは正規分布の確率密度の定義はDistributions.Gammaを使います。νとαが与えられれば、**Gamma(ν,1/α)**で定義します。juliaのAPIとガンマ分布の定義が少しずれているので、頭の体操が必要です。
using Plots
using Distributions
using StatPlots
v=100
a=1/5
d=Gamma(v, a)
plot(d,fill=(0, .5,:orange))
println("F(10) = ", cdf(d,10))
println("F(15) = ", cdf(d,15))
println("F(20) = ", cdf(d,20))
println("F(25) = ", cdf(d,25))
println("F(30) = ", cdf(d,30))
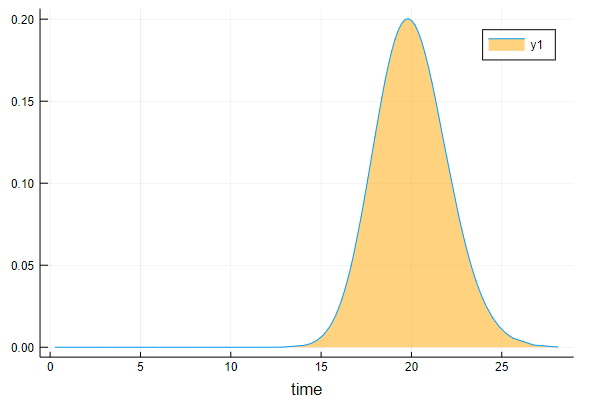
plot(d,fill=(0, .5,:orange),xlabel = "time")
分布の出力は以下のようになります。
F(10) = 3.200065324585125e-10 # 10分で100人来る確率 ほぼゼロ
F(15) = 0.0033524414981869707 # 15分で100人来る確率 ちょっとだけ
F(20) = 0.5132987982791488 # 20分で100人来る確率 50%の確率
F(25) = 0.990620868331174 # 25分で100人来る確率 99%の確率
F(30) = 0.9999940754596646 # 30分で100人来る確率 ほぼ1に近い
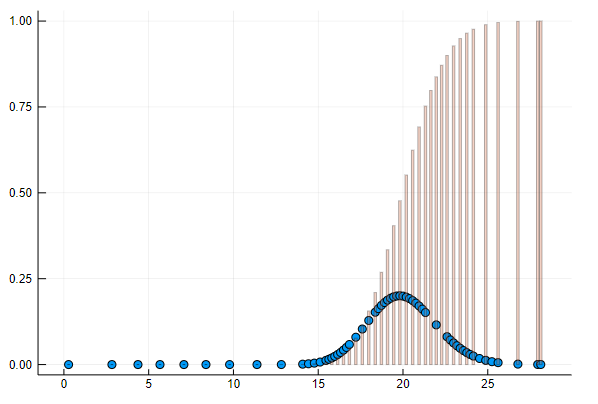
確率密度関数と分布のグラフです。
v=100
a=1/5
d=Gamma(v, a)
scatter(d, leg=false) # 確率密度関数 散布図
bar!(d, func=cdf, alpha=0.3) # 分布 棒グラフ
今回は以上です。