Juliaで学ぶ確率変数(4) - ポアソン分布（離散型）

Juliaで学ぶ確率変数(1) - 確率変数の定義 - Qiita
Juliaで学ぶ確率変数(11) - まとめ - Qiita

　確率変数を勉強中ですが、**「確率統計」（森北出版）は数学的に明確な定義がしっかり書かれているので、これを中心に勉強しています。あわせて「統計学入門」（東京大学出版会）と「確率論入門」（ちくま学芸文庫、赤攝也）**も併読しています。

　本記事は、それらの教科書を読みながら、実際に例題や問題をJuliaで解いていく試みです。Juliaの離散型確率変数のライブラリのドキュメントです。　==>Distributions/Univariate/DiscreteDistributions

#１．ポアソン分布 Po(λ)

以下のような偶然に起きる現象の回数は近似的にポアソン分布に従うと考えられています。

• １日に起こる交通事故の件数、
• １日に来るメールの数、
• コンサートチケットのキャンセル件数、
• ある時間帯の飲食店への来客数

以下にポアソン分布の定義を示します。ポアソンの小数法則が示すように、ポアソン分布は2項分布の近似であるという側面を持ちます。つまり２項分布B(n;p)において、npが一定で、nが十分に大きく、pが十分小さい状況を考える。このとき、２項分布の確率密度関数f(k)は、λ=npのポアソン分布で近似できます。

\begin{align}
\\
\\
&X : \Omega \rightarrow \{0,1,2...\}\\
&f(k)=e^{-\lambda}\frac{\lambda ^k}{k!} \qquad (k=0,1,2,...)、\lambda は正の定数\\
\\
&f : 0 \rightarrow e^{-\lambda}\\
&f : 1 \rightarrow e^{-\lambda} {\lambda}\\
&...\\
&f : k \rightarrow e^{-\lambda} \frac{\lambda^k}{k!}\\
&...\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad \\
\end{align}

ポアソン分布の平均と分散を示しておきます。

\begin{align}
&E[X] = \lambda\\
&V[X] = \lambda\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad \qquad \\
\end{align}

##１－１．ポアソンの小数法則

二項分布B(k;n,p)の近似式としてのポアソン分布です。

\begin{align}
&二項分布の平均値npに関して、一定値 \lambda を \lambda = np とおくとき、\\
&以下が成り立つ。\\

&\lim_{p \to 0} B(k;n,p) = e^{-\lambda}\frac{\lambda ^k}{k!}\\
\\
\\
&つまり平均値\lambdaの２項分布は、p \rightarrow 0、のとき、\\
&限りなくポアソン分布Po(λ)に近づく、といえる。\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad  \qquad \\
\end{align}

つまり、平均値npだけが計算できて、個々のnやpが必ずしも明らかではない場合、pが十分小さい値と想定できれば、ポアソン分布を使って２項分布の代わりとすることができます。

Juliaでどの程度の近似になっているのかを試してみます。結構、驚くほどいい感じで近似しています。

using Distributions

# ２項分布の確率密度関数の定義
n=200  # nを十分大きくとる
p=1/100  # pを十分小さくとる
d1= Distributions.Binomial(big(n), big(p))

# ポアソン分布の確率密度関数の定義
l=n*p   # 平均値だけわかればよい
d2=Poisson(l)


pdf.(d1,0:10)   # ２項分布の出力
 0.13397967485796192   
 0.2706660098140646    
 0.2720330098636306    
 0.18135533990908706   
 0.09021970192447003   
 0.035723356721608354  
 0.011727364580325972  
 0.0032829851783307885 
 0.0008000203780528317 
 0.00017239496362081214
 3.326003843593452e-5  

pdf.(d2,0:10)   # ポアソン分布の出力
 0.1353352832366127    
 0.2706705664732254    
 0.2706705664732254    
 0.18044704431548364   
 0.09022352215774178   
 0.03608940886309671   
 0.012029802954365572  
 0.0034370865583901616 
 0.0008592716395975415 
 0.00019094925324389769
 3.81898506487796e-5

ポアソンの小数法則によって、２項分布のモデルの問題をポアソン分布で解くことができます。しかも平均値だけがわかっていればいいのです。（nが大きくて、pが小さい、という条件は必要）。以下にポアソン分布を適用する例を見ていきます。

##１－２．コンサートチケットのキャンセル数

\begin{align}
&n人がチケットを購入 \leftarrow nは十分に大きい\\
&p:キャンセルの確率  \leftarrow pは十分に小さい\\
&2項分布のモデルで考える。\\
\\
&\Omega = \{0,1\} \qquad 1=キャンセル、0=キャンセルしない\\
&***根元事象は人ではなく、その人がキャンセルするか、しないか、である。\\
&***例えば、くじ引きの場合の根元事象は、くじそのものではなく、\\
&***1等か２等かの等級である。\\
&つまりキャンセルする事象をE=\{1\}と表す。当然、E^c=\{0\}\\
&チケットを購入したn人に対して確率変数を定義する。\\
&X_i^{(n)}(a_1,a_2,...,a_n) = 
\left\{
\begin{array}{ll}
1 & (a_i \in E) \\
0 & (a_i \notin E)
\end{array}
\right.\\
\\

&S^{(n)} : \Omega^{(n)} \rightarrow \{0,1,...,n\}\\
&S^{(n)} = X_1^{(n)} + X_2^{(n)} +...+ X_n^{(n)}\\
\\
&つまり、S^{(n)}(a_1,a_2,...,a_n) = k \;は以下のことを意味する。\\
&a_1,a_2,...,a_nのうちチケットをキャンセルする人数がk人である。\\
&（Eに属する個数がk個。）\\
\\
&ポアソンの小数法則によって、λ=np 定数とすれば、\\
&キャンセルする人数はポアソン分布に従う。\\
\\
&つまり、過去の統計からキャンセルの平均値さえわかれば、\\
&キャンセル数ごとの確率が計算できます。\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad  \qquad   \qquad \qquad   \\
\end{align}

１日に来るメールの数
同じようにして解ける。

• n人：A君にメールを送る可能性のある人の数
• p:それぞれがメールを送る確率
• λ=np 定数とすれば、メールを送る人数はポアソン分布に従う

##１－３．休日ある時間帯の飲食店への来客数

\begin{align}

&n人；休日のある時間帯に街に出かかる人の人数 <=nは十分に大きい\\
&m店：ランチを提供するレストラン数\\
&\lambda 人：=  １店の平均人数 \; ( \lambda = n/m )\\
&p：どこのレストランに入るかの確率 (p=1/m)\\
\\
&2項分布のモデルで考える。\\
\\
&\Omega = \{a_1,a_2,...,a_n\}\\
&Eをある店に来店する事象。\\
&\Omega = \{0,1\} \qquad 1=来店する、0=来店しない\\
&***根元事象は人ではなく、その人が来店するか、しないか、である。\\
&***例えば、くじ引きの場合の根元事象は、くじそのものではなく、\\
&***1等か２等かの等級である。\\
&つまり来店する事象をE=\{1\}と表す。当然、E^c=\{0\}\\
&街に出かけたn人に対して確率変数を定義する。\\
&X_i^{(n)}(a_1,a_2,...,a_n) = 
\left\{
\begin{array}{ll}
1 & (a_i \in E) \\
0 & (a_i \notin E)
\end{array}
\right.\\
\\

&S^{(n)} : \Omega^{(n)} \rightarrow \{0,1,...,n\}\\
&S^{(n)} = X_1^{(n)} + X_2^{(n)} +...+ X_n^{(n)}\\
\\
&つまり、S^{(n)}(a_1,a_2,...,a_n) = k \;は以下のことを意味する。\\
&a_1,a_2,...,a_nのうちある店に来店する人数がk人である。\\
&（Eに属する個数がk個。）\\
\\
&ここまでは2項分布のモデルですが、ポアソンの小数法則によって、\\
&λ=np 定数とすれば、あるレストランに来店する人数はポアソン分布に従う。\\
&つまり来店する人数ごとの確率が計算できる。\\
\\
\\
\\
&\qquad \qquad  \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad \qquad \qquad  \qquad \qquad  \qquad \qquad \qquad  \qquad \qquad  \qquad \\
\end{align}

具体的な数字を当てはめて考えてみます。

全人数 n=10,000人
お店の数 m=200店
平均来店数 λ=n/m=50人
来店の確率 p=1/m=1/200

ポアソン分布で必要なのは平均来店数（50人）だけです。

using Plots
using Distributions
using StatPlots

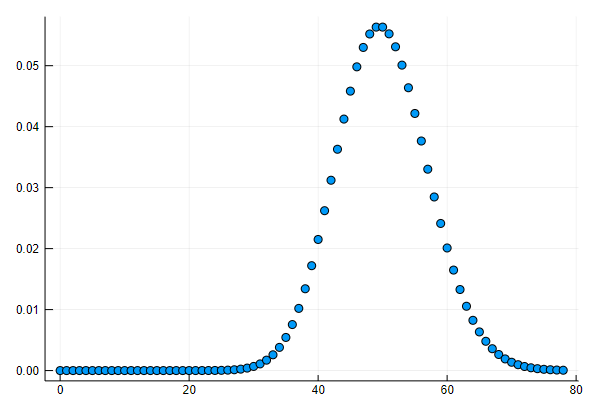
d = Poisson(50) 
scatter(d, leg=false) 

分布図は以下のようになります。

当然ですが、ここで仮定されているのは、n人の人が全くランダムにお店を選択すればという前提です。たまたま中華が好きな人が多いとか、焼き肉好きが多いとか、ということは排除されます。

##１－４．Juliaで例題を解いてみる(1)

Juliaで分布を扱うための基礎知識は以下のページを参照してください。
「Juliaで学ぶ確率変数(1) - 確率変数の定義」の「４．Juliaで確率分布を扱う」

JuliaではDistributions.Poissonを使います。

「確率論入門」（ちくま学芸文庫、赤攝也）で紹介されていた、以下の有名な例を考えてみます。

ボルトキエヴィッチは、プロシャの延べ200個の軍団のおのおのについて、1年間のうちに馬にけられて死亡した兵士の数kを記録し、下のような表にまとめた。

k	0	1	2	3	4	5以上
軍団の数	109	65	22	3	1	0

これは例えば、兵士1人が死んだ軍団の数が109個あるという表です。
平均値を求めてみます。

\frac{0*109+1*65+2*22+3*3+4*1}{200} = 0.61

平均値が分かったので、逆にポアソン分布を使って、Juliaで確率密度を計算してみる。

import Pkg; Pkg.add("Distributions")
using Distributions
d=Poisson(0.61)
pdf.(d,0:5)*200

 108.67017381489997   
  66.28880602708898   
  20.218085838262144  
   4.111010787113301  
   0.6269291450347785 
   0.07648535569424297

以下のような表が得られました。オリジナルとほぼ一致します。不思議ですね。

k	0	1	2	3	4	5以上
軍団の数	108.7	66.2	20.2	4.1	0.6	0

参考までにPlotしてみます。

using Plots
using Distributions
using StatPlots

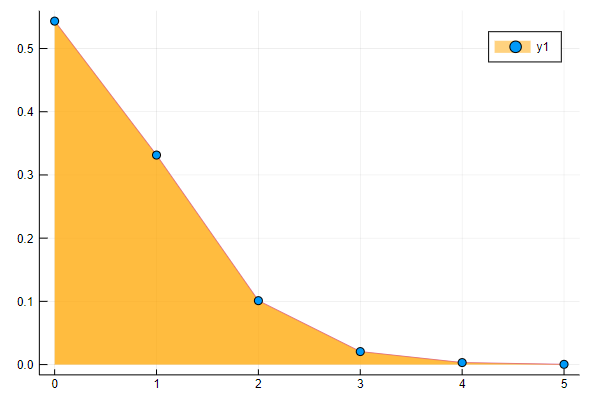
d=Poisson(0.61)
plot(d,fill=(0, .5,:orange))

（補足）Juliaでは破壊的な関数の名前に ! をつけるのが慣習です。

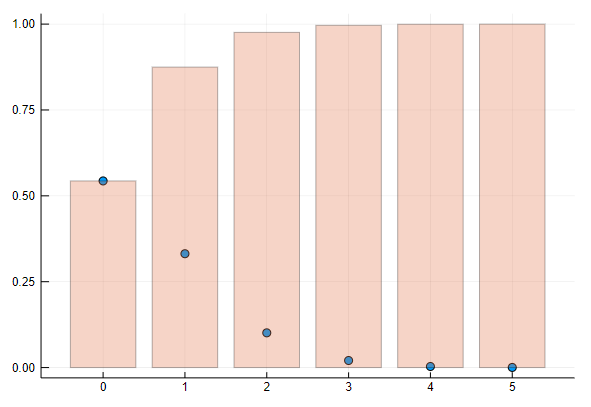
scatter(d, leg=false)         # 確率密度を散布図にする
bar!(d, func=cdf, alpha=0.3)  # 分布を棒グラフにする

##１－５．Juliaで例題を解いてみる(2)

あるビジネスマンには、平日午後１時から２時までの間の１時間に、平均８通の電子メールが来るという。この１時間に届く電子メールの数Xがポアソンの分布に従うとみなせるとき、届く電子メールが３通未満である確率を求めよ。

E[X]=8 なのでポアソン分布 Po(8)で計算できる。

using Plots
using Distributions
using StatPlots

d = Poisson(8)  # 平均値=8のポアソン分布
cdf(d,2)        # ３通未満の確率
0.013753967744002994

ポアソン分布の確率密度の散布図を描く
（補足）Juliaでは破壊的な関数の名前に ! をつけるのが慣習です。

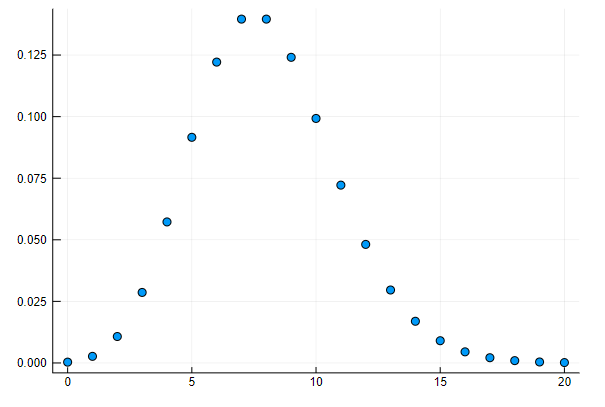
scatter(d, leg=false)         # 確率密度を散布図にする

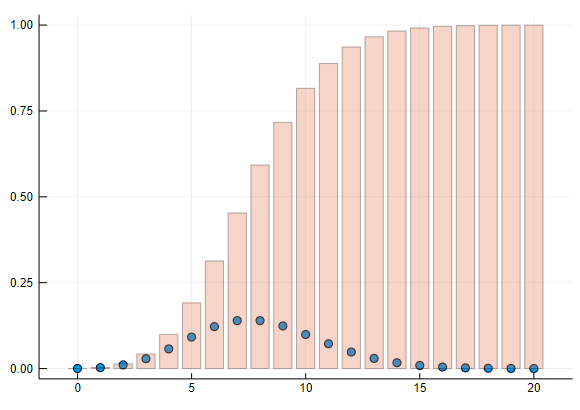
ポアソン分布の確率密度の散布図と分布の棒グラフを描く

scatter(d, leg=false)         # 確率密度を散布図にする
bar!(d, func=cdf, alpha=0.3)  # 分布を棒グラフにする

##１－６．Juliaで例題を解いてみる(3)

ある果樹園から市場に出荷されるミカンの中には、どうしても0.1%は傷んだものが混ざってしまうという。果樹園から市場へ1000個のミカンを出荷したとき、３個以上のミカンが傷んでいる確率を概算せよ。

ミカンが傷んだ個数の確率変数Xは、n=1000, p=0.001の２項分布に従うと思われる。しかし(1-p)^999=0.999^9999の計算などを手計算でもとめるのは無理があります。ポアソン分布で近似を求めるのが現実的です。しかもここではポアソン分布をJuliaで計算してみます。

using Plots
using Distributions
using StatPlots

n=1000
p=0.001

d = Poisson(n*p)  # （２項分布の）平均値=n*p のポアソン分布
1-cdf(d,2)        # 1-（2個以下の確率）

0.08030139707139416  # ３個以上のミカンが傷んでいる確率

0-5の範囲の確率密度関数の値を表示させます。

pdf.(d,0:1:5)   # 0-5の範囲の確率密度関数の値

 0.36787944117144233  
 0.36787944117144233  
 0.18393972058572114  
 0.06131324019524039  
 0.015328310048810105 
 0.0030656620097620196

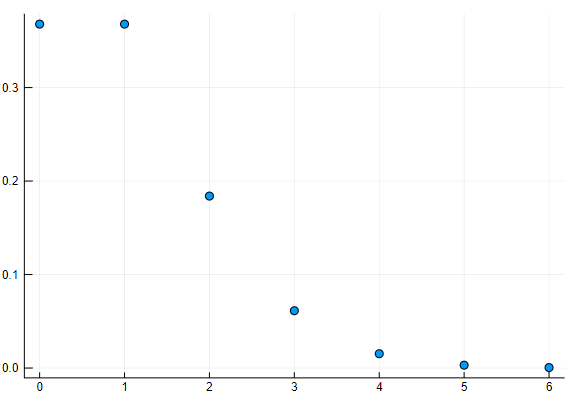
ポアソン分布の確率密度の散布図を描く
（補足）Juliaでは破壊的な関数の名前に ! をつけるのが慣習です。

scatter(d, leg=false)         # 確率密度を散布図にする

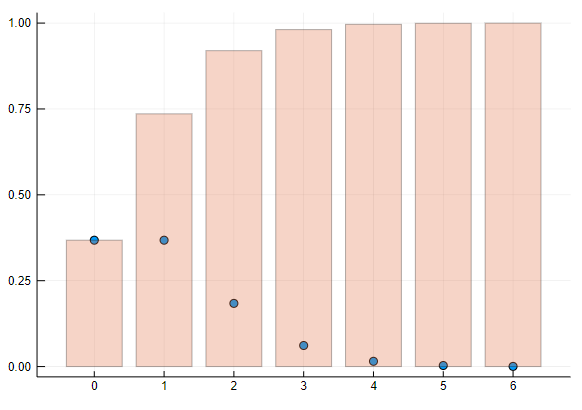
ポアソン分布の確率密度の散布図と分布の棒グラフを描く

scatter(d, leg=false)         # 確率密度を散布図にする
bar!(d, func=cdf, alpha=0.3)  # 分布を棒グラフにする

今回は以上です。