Juliaで学ぶ確率変数(1) - 確率変数の定義 - Qiita
Juliaで学ぶ確率変数(11) - まとめ - Qiita
確率変数を勉強中ですが、**「確率統計」(森北出版)は数学的に明確な定義がしっかり書かれているので、これを中心に勉強しています。あわせて「統計学入門」(東京大学出版会)と「確率論入門」(ちくま学芸文庫、赤攝也)**も併読しています。
本記事は、それらの教科書を読みながら、実際に例題や問題をJuliaで解いていく試みです。Juliaの連続型確率変数のライブラリのドキュメントです。 ==>Distributions/Univariate/ContinuousDistributions
1.指数分布 Ex(λ)
指数分布 Ex(λ)は、『連続的な待ち時間分布』と呼ばれ、期間1/λあたりに1回起きると期待される事象が1回起きるまでの時間の分布、という意味を持つとされています。幾何分布と同じく待ち時間分布という性質を持っています。機械の部品などの故障時間の分布として使われることが多い。
\begin{align}
\\
\\
&\lambdaを正の定数とする。\\
\\
&X: \Omega \rightarrow 非負の実数値\\
\\
&確率密度関数f(x)が以下のように書けるとき、Xは指数分布Ex(\lambda)に従うという。\\
\\
&f(x) =
\left\{
\begin{array}{ll}
\lambda e^{-\lambda x} & (x \geqq 0 \;のとき) \\
0 & (x<0\;のとき)
\end{array}
\right.\\
\\
\\
&ここで、以下が成り立つ。\\
&p(\Omega)=\int_{-\infty}^{\infty} f(x) dx = \int_{0}^{\infty} \lambda e^{-\lambda x} dx = 1\\
&E[X] = \int_{0}^{\infty} xf(x) dx = \frac {1} {\lambda}\\
&V[X] = \int_{0}^{\infty} (x - E[X])^2 f(x) dx = \frac {1} {\lambda^2}\\
&F(x) = p(\{X \leqq x\})
= \int_{-\infty}^{x} f(t) dt
= \int_{0}^{x} \lambda e^{-\lambda t} dt = 1-e^{-\lambda x}\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-1.p(Ω)の証明
解析学の練習にp(Ω)とE[X]、F(x)の証明を追ってみたいと思います。「確率統計」(森北出版)の証明は全く分からなかったので、「改訂版 解析学大要」(養賢堂)で解析学を復習しつつ試みました。
\begin{align}
\\
&p(\Omega)=\int_{-\infty}^{\infty} f(x) dx = \int_{0}^{\infty} \lambda e^{-\lambda x} dx\\
\\
&上の定義から以下を導きます。\\
&p(\Omega) = 1\\
\\
\\
&まず \; x=\varphi(t) = -\frac{t}{\lambda} \; とすると、t = -\lambda x となります。\\
&\varphi(0)=0,\; \varphi(-\infty)=\infty \; であるから、置換積分により、\\
&p(\Omega) = \int_{0}^{\infty} \lambda e^{-\lambda x} dx
= \lambda \int_{0}^{-\infty} e^{t} \frac{dx}{dt} dt
= \lambda \int_{0}^{-\infty} e^{t} \frac{-1}{\lambda} dt \\
&= -\int_{0}^{-\infty} e^{t} dt
= -[e^t]_0^{-\infty}\\
\\
\\
&一般に、\lim_{x \to -\infty} e^x = 0,\; e^0=1が成り立つから、\\
\\
&p(\Omega) = -(0-1)=1 \qquad \qquad Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-2. E[X]の証明
\begin{align}
\\
&E[X]=\int_{0}^{\infty} xf(x) dx = \int_{0}^{\infty} x \lambda e^{-\lambda x} dx\\
\\
&上の定義から以下を導きます。\\
&E[X] = \frac {1} {\lambda}\\
\\
\\
&まず \; x=\varphi(t) = \frac{t}{\lambda} \; とすると、t = \lambda x となります。\\
&\varphi(0)=0,\; \varphi(\infty)=\infty \; であるから、置換積分により、\\
&E[X] = \int_{0}^{\infty} x \lambda e^{-\lambda x} dx = \int_{0}^{\infty} t e^{-t} \frac{dx}{dt} dt =\int_{0}^{\infty} t e^{-t} \frac{1}{\lambda} dt = \frac{1}{\lambda} \int_{0}^{\infty} t e^{-t} dt \\
\\
&また\frac{d\;(-e^{-t})}{dt}=e^{-t}だから、部分積分により、\\
&\lambda \; E[X] = \int_{0}^{\infty} t e^{-t} dt
= \int_{0}^{\infty} t \frac{d\;(-e^{-t})}{dt} dt\\
&= [t(-e^{-t})]_0^\infty - \int_{0}^{\infty} (-e^{-t})dt \\
&= [t(-e^{-t})]_0^\infty - [e^{-t}]_0^\infty\\
\\
&一般に、\lim_{x \to -\infty} e^x = 0,\; \lim_{x \to \infty} xe^{-x} = 0 ,\; e^0=1が成り立つから、\\
&\lambda \; E[X] = 0 - (-1) = 1
\\
&よって \; E[X]=\frac {1} {\lambda} \qquad \qquad Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
1-3.F(x)の証明
\begin{align}
\\
&F(x) = p(\{X \leqq x\})
= \int_{-\infty}^{x} f(t) dt
= \int_{0}^{x} \lambda e^{-\lambda t} dt\\
\\
&上の定義から以下を導きます。\\
&F(x) = 1-e^{-\lambda x}\\
\\
\\
&「1-1.P(\Omega)の証明」と同じようにして以下が成り立つ。\\
\\
&まず \; t=\varphi(s) = -\frac{s}{\lambda} \; とすると、s = -\lambda t となります。\\
&\varphi(0)=0,\; \varphi(-\lambda x)=x \; であるから、置換積分により、\\
&F(x) = \int_{0}^{x} \lambda e^{-\lambda t} dt
= \lambda \int_{0}^{-\lambda x} e^{s} \frac{dt}{ds} ds
= \lambda \int_{0}^{-\lambda x} e^{s} \frac{-1}{\lambda} ds \\
&= -\int_{0}^{-\lambda x} e^{s} ds
= -[e^s]_0^{-\lambda x}=1-e^{-\lambda x}\\
\\
&Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\end{align}
計算するとき便利でした。==>「数列の極限」
1-4.Juliaで解く例題(1)
Juliaで分布を扱うための基礎知識は以下のページを参照してください。
「Juliaで学ぶ確率変数(1) - 確率変数の定義」の「4.Juliaで確率分布を扱う」
以下のサイトの例題を考えてみます。
[練習問題(15. いろいろな確率分布3)- 統計WEB]
https://bellcurve.jp/statistics/course/8282.html
--- 問題 ---
Kさんのもとには、日々たくさんのお問い合わせメールが届く。お問い合わせメールに対する返信メールの作成時間は1通あたり平均15分の指数分布に従うと仮定できる。
1.作成時間が30分以上となる確率を求めよ。
2.また、作成時間が5分以上10分以下となる確率を求めよ。
--- 解答 ---
\begin{align}
&まず\lambdaを求めます。指数分布の期待値の公式より、E[X]=\frac{1}{\lambda}=15なので、\\
&\lambda=\frac{1}{15}と求められます。\\
\\
\\
&メールの作成時間が30分以下となる確率は、分布F(30)と表現できます。\\
&F(30) = 1-e^{-\lambda 30} = 1-e^{-\frac{1}{15} 30}= 1-e^{-2}\\\
\\
&作成時間が30分以上となる確率は、余事象の確率で、1-F(30)、となります。
\\
\\
\\
&作成時間が5分以上10分以下となる確率は分布で、F(10) - F(5)、となります。\\
&F(10) - F(5) = (1-e^{-\lambda 10}) - (1-e^{-\lambda 5}) = e^{-\frac{1}{15} 5}-e^{-\frac{1}{15} 10}\\
\\
\\
&これ以上の具体的な計算は、Juliaに任せます。\\
&Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\\
\end{align}
--- Juliaの計算 ---
JuliaのパッケージDistributionsでは、確率密度関数(Probability Density Function = PDF)の評価はpdf関数でした。分布(累積分布関数) (Cumulative Distribution Function = CDF)の評価はcdf関数を使います。
Distributions.cdf — Method.
cdf(d::UnivariateDistribution, x::Real)
Evaluate the cumulative probability at x.
Juliaでは正規分布の確率密度の定義はDistributions.Exponentialを使います。\lambdaが与えられれば、**Exponential(1/lambda)**で定義します。Exponential(lambda)でないことに注意してください。
using Plots
using Distributions
using StatPlots
d=Exponential(15)
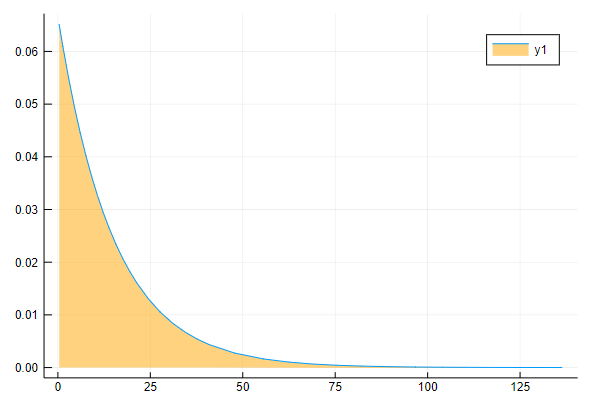
plot(d,fill=(0, .5,:orange))
println("F(30) = ", cdf(d,30))
println("1 - F(30) = ", 1-cdf(d,30))
println("F(10) - F(5) = ", cdf(d,10) -cdf(d,5))
plot(d,fill=(0, .5,:orange))
出力は以下のようになります。
F(30) = 0.8646647167633873 # メールの作成時間が30分以下となる確率
1 - F(30) = 0.1353352832366127 # 作成時間が30分以上となる確率
F(10) - F(5) = 0.20311419154119725 # 作成時間が5分以上10分以下となる確率
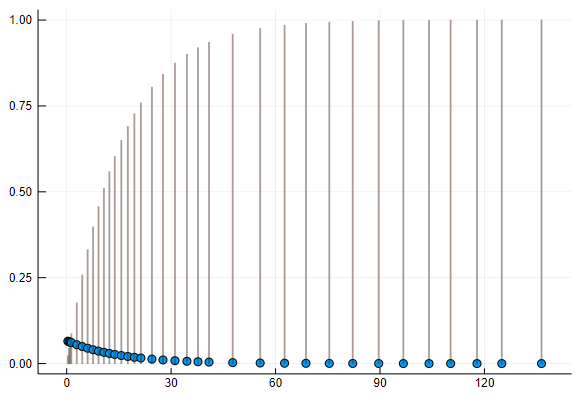
確率密度関数と分布の関係をグラフで表します。
d=Exponential(15)
scatter(d, leg=false) # 確率密度関数
bar!(d, func=cdf, alpha=0.3) # 分布
1-5.Juliaで解く例題(2)
「確率統計」(森北出版)にある例題です。
--- 問題 ---
ある機械がx時間以内に故障する確率F(x)が以下の式で与えられているとする。
$$F(x)=1-e^{-\frac{x}{100}} \qquad (x>0)$$
1.機械が故障するまでの時間X従う分布と確率密度関数を求めよ。
2.機械が故障するまでの時間の平均E[X]と分散V[X]を求めよ。
3.この機械が故障するまでの時間が200時間を超える確率pを求めよ。
--- 解答 ---
\begin{align}
&1.まず分布の定義と問題の条件より、\\
&F(x) = p(\{X \leqq x\})= 1-e^{-\frac{x}{100}} \qquad (x>0)\\
\\
&ゆえに確率密度関数f(x)は以下のようになる。\\
&f(x) = \frac{d \; F(x)}{dx} = \frac{1}{100} e^{-\frac{x}{100}}\\
\\
&つまり\lambda = \frac{1}{100}として、Xは指数分布E_x(\frac{1}{100})に従うと言える。\\
\\
\\
\\
&2.\lambda = \frac{1}{100}だから、\\
&E[X] = \frac {1} {\lambda} = 100\\
&V[X] = \frac {1} {\lambda^2} = 10000\\
\\
\\
\\
&3.200時間までに機械が故障する確率はF(200)で表される。\\
&求める確率は余事象の確率なので、p=1-F(200)となる。\\
\\
\\
&これ以上の具体的な計算は、Juliaに任せます。\\
&Q.E.D.\\
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \\
\\
\end{align}
--- Juliaの計算 ---
using Plots
using Distributions
using StatPlots
d=Exponential(100)
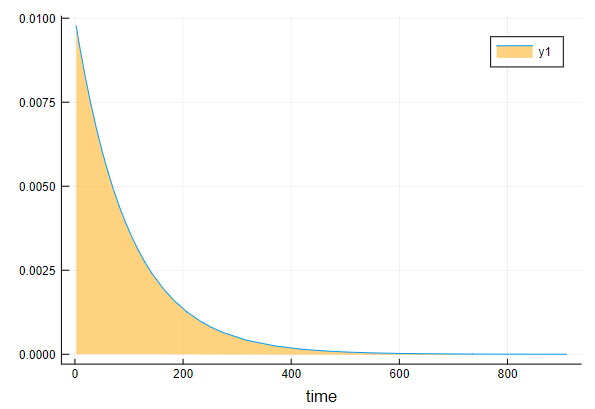
plot(d,fill=(0, .5,:orange))
println("F(200) = ", cdf(d,200))
println("1 - F(200) = ", 1-cdf(d,200))
plot(d,fill=(0, .5,:orange),xlabel = "time")
出力は以下のようになります。
F(200) = 0.8646647167633873 # 200時間までに機械が故障する確率
1 - F(200) = 0.1353352832366127 # 故障するまでの時間が200時間を超える確率
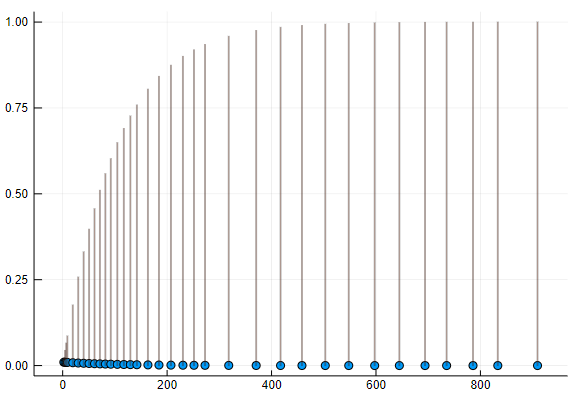
確率密度関数と分布の関係をグラフで表します。
d=Exponential(100)
scatter(d, leg=false) # 確率密度関数
bar!(d, func=cdf, alpha=0.3) # 分布
今回は以上です。