Juliaをはじめてみる

　Julia言語が正式リリースされたことで早速使ってみました。Juliaは科学計算に特化した言語で2009年に開発が始まり、2012年に初公開されてから、やっと10年の月日を経て2018年8月に1.0がリリースされたものです。MITの4人の研究者が開発をはじめ、科学計算に焦点を当てて開発されていますが、あくまでも汎用言語です。やはりMITで様々なプロジェクトに使用されてきたようです。例えばWebフレームワークなどのライブラリもあります。

　そうすると当然、Pythonとは大きく領域が被りますが、julia言語の差別化はズバリ速度です。ザックリ言ってC言語より2倍遅く（10倍や100倍ではない）、Pythonより10倍、30倍速いということが言われています。kerasを使って1日2日かかっていた学習を数時間で終わらせることができるかも、という期待が胸を横切ります。はじめから機械学習は言語開発のターゲットになっているので、FluxやKnet、Mochaなどのフレームワークが存在します。TensorFlowのラッパーもあります。その他の科学計算のためのライブラリも充実しているようなので、勉強のお供によいですね。

「Julia 1.0」がリリース--急成長を見せるMIT開発のプログラミング言語
https://japan.techrepublic.com/article/35125276.htm

#インストール

　Windows10のパッケージ「Current stable release (v1.0.1)」をダウンロードしインストールします。jupyter notebook(anaconda)は既にインストール済みなので、その環境にマージします。

　Juliaのインストールが終わったら、環境変数のPathに追加します。
C:\Users\user123\AppData\Local\Julia-1.0.1\bin

（jupyter notebookを全然使いこなしてませんが、今回はjupyterlabの方を使います。）

　以下の操作でAnacondaを更新します。（jupyterlabも最新になる）
Anaconda Promtを「管理者として実行」（右クリック）し、以下のコマンドを打つ

conda update --all

　IJuliaをインストールするために、コマンドプロンプトからjuliaを起動して以下を実行します。これでjupyterにjuliaが追加されます。

using Pkg
Pkg.add("IJulia")
using IJulia

　juliaの追加を確認するために、Anaconda Promtを起動してjupyter kernelspec listを打ちます。

(base) C:\Users\user123>jupyter kernelspec list
Available kernels:
  julia-1.0    C:\Users\user123\AppData\Roaming\jupyter\kernels\julia-1.0
  python3      C:\ProgramData\Anaconda3\share\jupyter\kernels\python3

#２．動作確認

jupyter lab で起動し、動作を確認します。

###動作確認 Plots

　以下のようにPlotsのみをインストールすることによって、グラフを描くことができます。

import Pkg
Pkg.add("Plots")
using Plots
gr()
plot(randn(100,3))

###動作確認 Statistics

　標準ライブラリStatisticsを使って、標準偏差（std)や分散(var)の関数が使えます。確認してみましょう。

using Statistics
mean(1:20)
a=[71,80,89,80]
b=[77,80,83,80]
std(a)
7.3484692283495345
std(b)
2.449489742783178
var(a)
54.0
var(b)
6.0

###動作確認 2項分布

　簡単な2項分布を計算してみます。

　今読んでいる「確率論入門」（ちくま学芸文庫、赤攝也）の例題を計算してみましょう。左利きの人が1%いる集団から1人選び、右利きか左利きかをみる。それを200回繰り返したときに4人以上が左利きである確率を計算する。2項分布を使って以下のように計算できます。

\sum_{i=4}^{200}
\begin{pmatrix} 200 \\i \end{pmatrix}
\left(\frac{1}{100}\right)^i
\left(\frac{99}{100}\right)^{200-i}

Julia言語のBaseのMathematicsカテゴリのbinomial関数を使います。BaseなのでMathematicsカテゴリの関数は特に何もしなくとも利用できます。
Mathematics
https://docs.julialang.org/en/v1/base/math/

function mybinomial(k, n, p)
    s = 0.0
    for i in k:n
        s += binomial(n,i)*(p)^i*(1-p)^(n-i)
    end
    s
end

mybinomial(4, big(200), big(1/100))

　0.141965965....というような値になります。参考書には0.143,,,とあり少し違うの気になります。PCの精度のちがい？

　mybinomial(4, 200, 1/100)で呼び出すとoverflowエラーとなります。big(200), big(1/100)とすると、Int64ではなくBigIntでの計算に切り替わりoverflowに陥りません。

　同じ問題を、Distributionsライブラリを使えば一発で計算できます。

using Distributions
d= Distributions.Binomial(big(200), big(1/100))
sum(pdf(d, 4:200))
0.14196596555525592

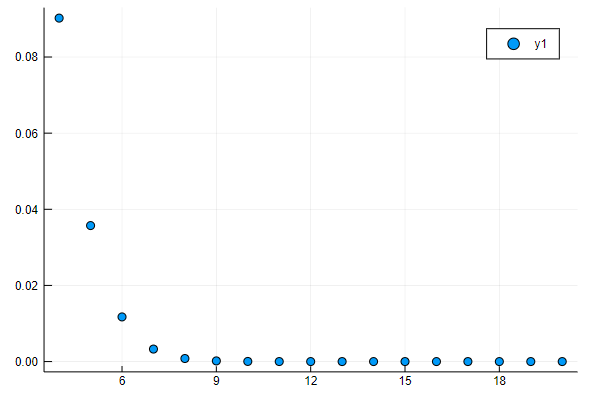
プロットしてみましょう。

plot(4:20, pdf(d,4:20), seriestype=:scatter)

　これからも確率統計の勉強のお供にjuliaを活用してきたいと思います。

以上です。