Plots.jlで線形計画問題の図的解法をやってみる

##はじめに

最近Juliaを使うようになって、グラフの出力にPlots.jlを使うのですが、いまひとつ思ったようにグラフの出力ができないで微妙に詰まったのでグラフの出力の練習に線形計画問題の図的解法をやってみることにしました。
今回出力するのは直線と直線で囲まれた領域です。

線形計画問題

次の問題を解いていきます。
$$
\begin{align*}
maximize ~ & ~ x_1 + 2x_2, \\
subject ~ to ~ & ~ x_1 + 3x_2 \leq 15, \\
& ~ x_1 + x_2 \leq 7, \\
& ~ 2x_1 + x_2 \leq 12, \\
& ~ x_1, x_2 \geq 0.
\end{align*}
$$

式を変形すると、実行可能領域を図示するのに必要な次の式が得られます。
$$
x_2 = -\frac{1}{3}x_1 + 5 \\
x_2 = -x_1 + 7 \\
x_2 = -2x_1 + 12 \\
0 \leq x_2 \leq f(x_1), ~ s.t. ~ f(x) =
\begin{eqnarray}
\begin{cases}
-\frac{1}{3}x + 5, ~ if ~ x \in [0, 3) & \\
-x + 7 ~ if ~ x \in [3, 5) & \\
-2x + 12 ~ if ~ x \in [5, 6] &
\end{cases}
\end{eqnarray}
$$

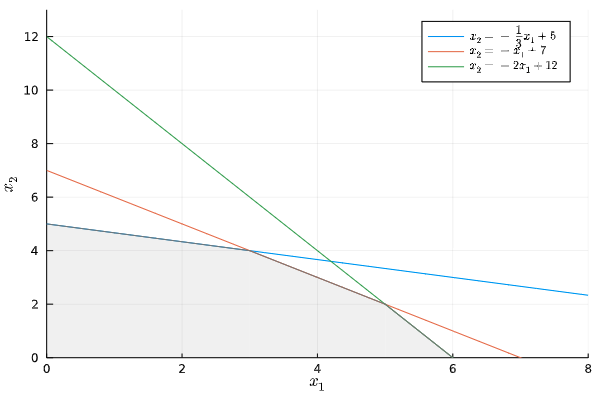
実行可能領域の図の出力

using LaTeXStrings
using Plots; plots.gr()

function plotRegion!(interval, f)
    Plots.plot!(
        interval,
        f,
        fillrange = 0,
        fillalpha = 0.1,
        c = :grey,
        label = ""
    )
end

function plotFeasibleRegion()
    Plots.plot(
        x -> (-(1/3)x + 5),
        xlims = (0, 8),
        ylims = (0, 13),
        xlabel = L"x_1",
        ylabel = L"x_2",
        label = L"x_2 = -\frac{1}{3}x_1 + 5"
    )
    Plots.plot!(x -> -x + 7, label = L"x_2 = -x_1 + 7")
    Plots.plot!(x -> -2x + 12, label = L"x_2 = -2x_1 + 12")
    plotRegion!(0:3, x -> -(1/3)x + 5)
    plotRegion!(3:5, x -> -x + 7)
    plotRegion!(5:6, x -> -2x + 12)
end

plotFeasibleRegion()

領域部分は凡例部分に出てほしくなかったので、label = ""を指定して凡例部分から消しました。
領域部分の描画は直線の交点が交わる$x_1$を境界にして3つに分割しました。

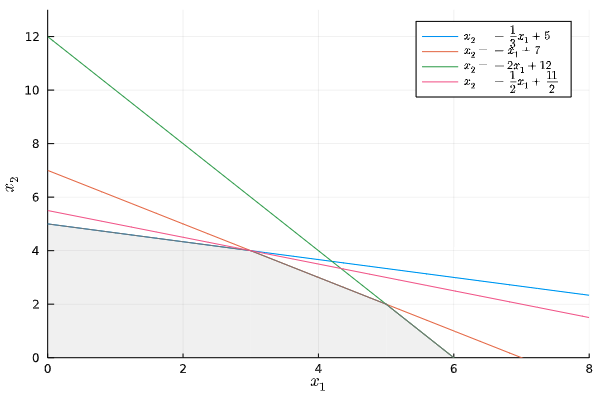
解の導出

最小化する関数を$k = x_1 + 2x_2$と置いて変形すると、$x_2 = -\frac{1}{2}x_1 + \frac{k}{2}$となり、この直線の傾きから直線が$(3, 4)$を通るとき，すなわち$x_1 = 3, x_2 = 4$が$k$が最大となる線形計画問題の最適解であるとわかります。

図示してみます。

plotFeasibleRegion()
plot!(x -> -(1/2)x + 11/2, label = L"x_2 = -\frac{1}{2}x_1 + \frac{11}{2}")

おわりに

LaTeXStringsの構文ハイライトが変になっていますが気にしないでください。
Julia使いはじめて日が浅いのでコードの中に改善できる点があるかもしれません。
何かありましたらコメントでのご指摘よろしくおねがいします。

バージョン等

Docker Image jupyter/datascience-notebook 2eac078be835
実行にJupyter Notebookを使用

Julia 1.6.0
Plots 1.11.2
LaTeXStrings 1.2.1

参考ページ