【図解】最難関Sランクの1問目「村人の友好関係」を解いてみた

はじめに

paiza×Qiita記事投稿キャンペーン「プログラミング問題をやってみて書いたコードを投稿しよう！」
というのをやってます。参加してみました。

やった問題

一番上にあった「村人の友好関係」というSランクの問題をやりました。

結果

100点でした。

解説

大量のデータの一部がちょこちょこと変わり、変わるごとに全体の最大値を答える問題です。
セグメント木で方針を立てます。
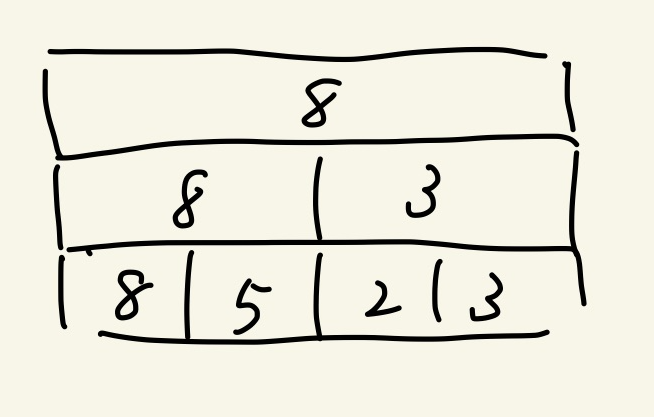
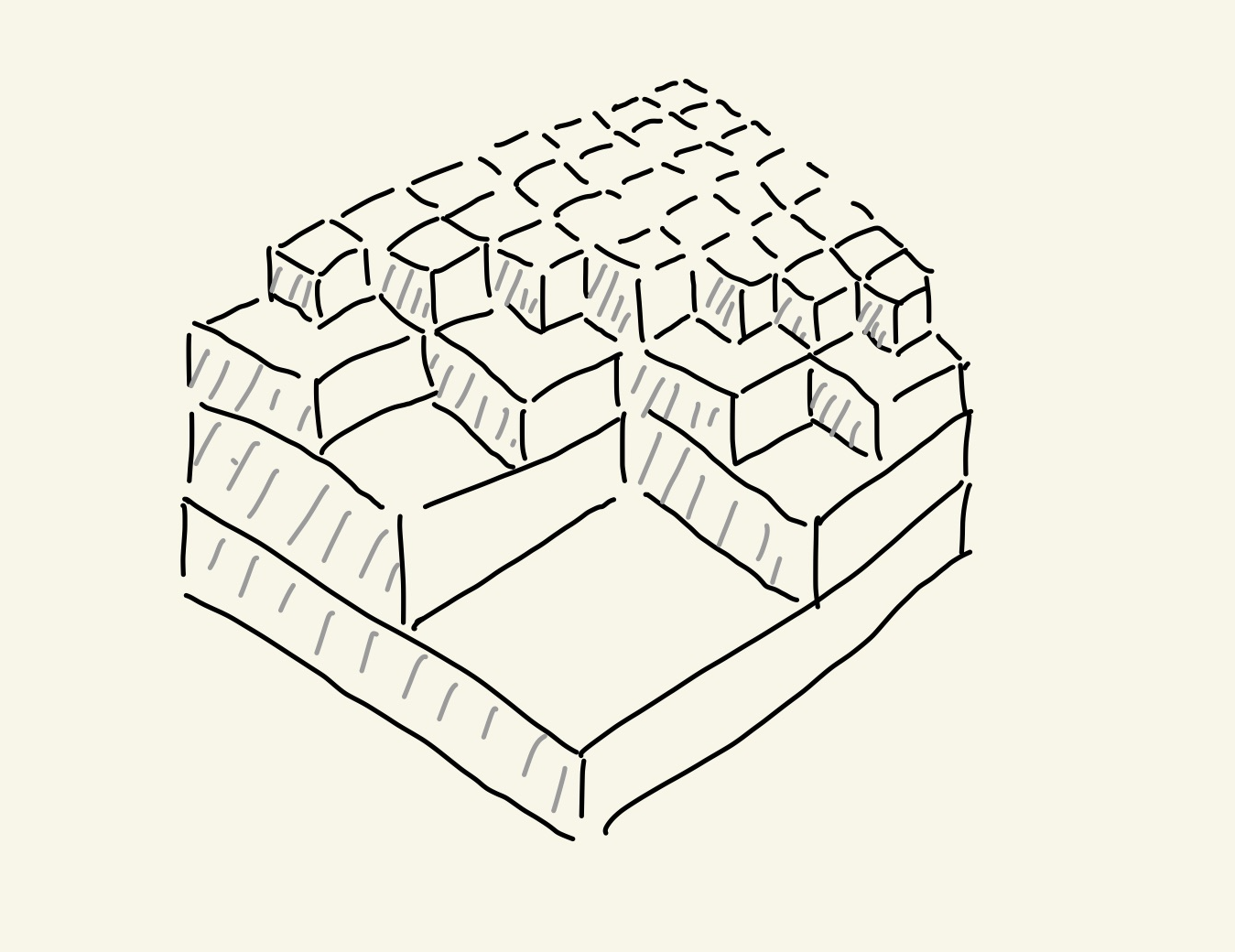
セグメント木はこういうものです。

上に乗っかっている積み木はその下の2つの最大値を保持します。
一番下の積み木は個々のデータです。
一番上の積み木は全体の最大値になります。
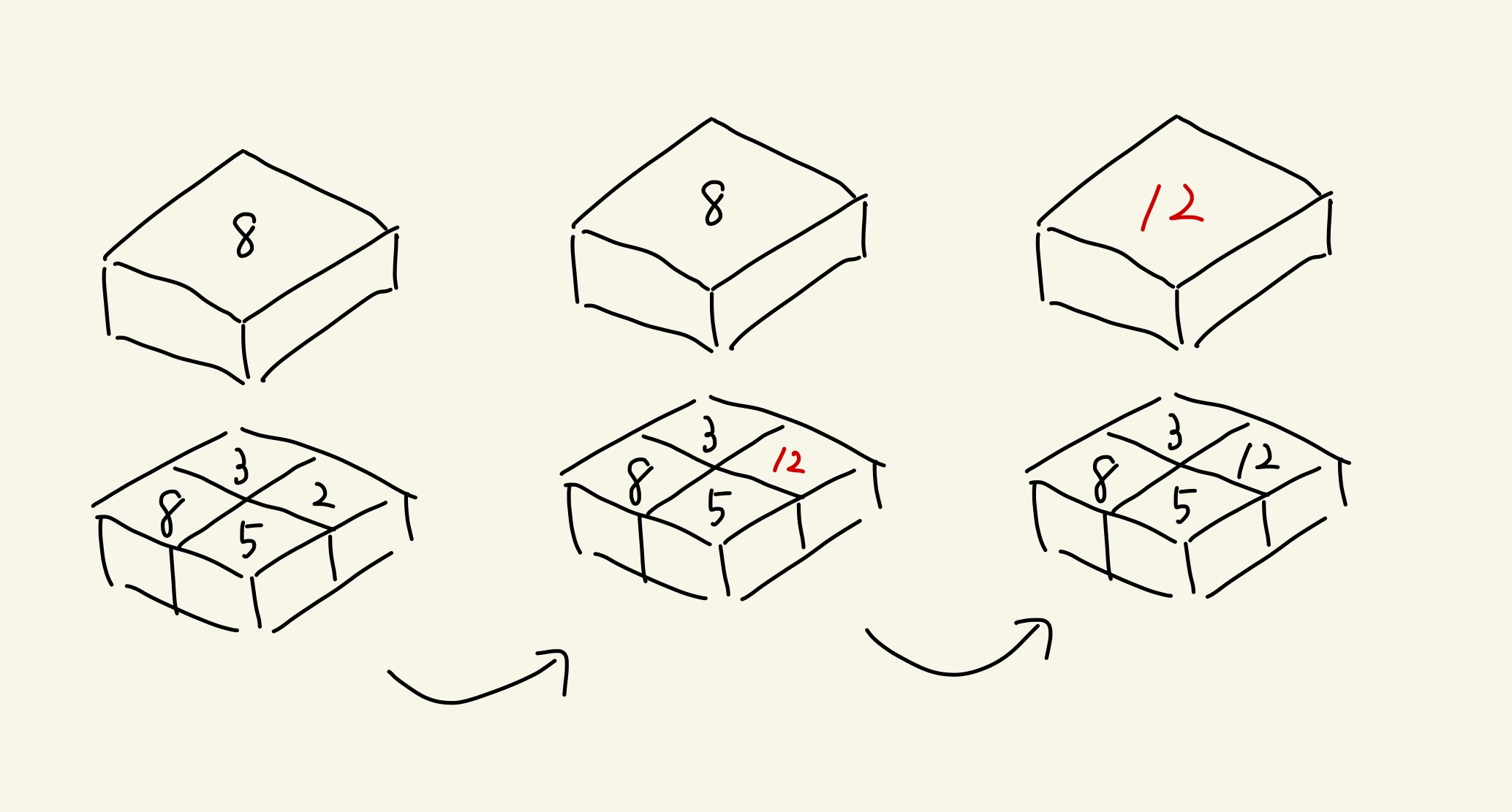
4つの値のどれかが変化するが、その都度全体の最大を答える問題ではこのように7つの積み木になります。

ある値を大きくしたときはこうなります。

ある値を小さくしたときはこうなります。

今回は「人Aと人Bの関係」というものが大量にあり、それが正の値か0かを取ります。
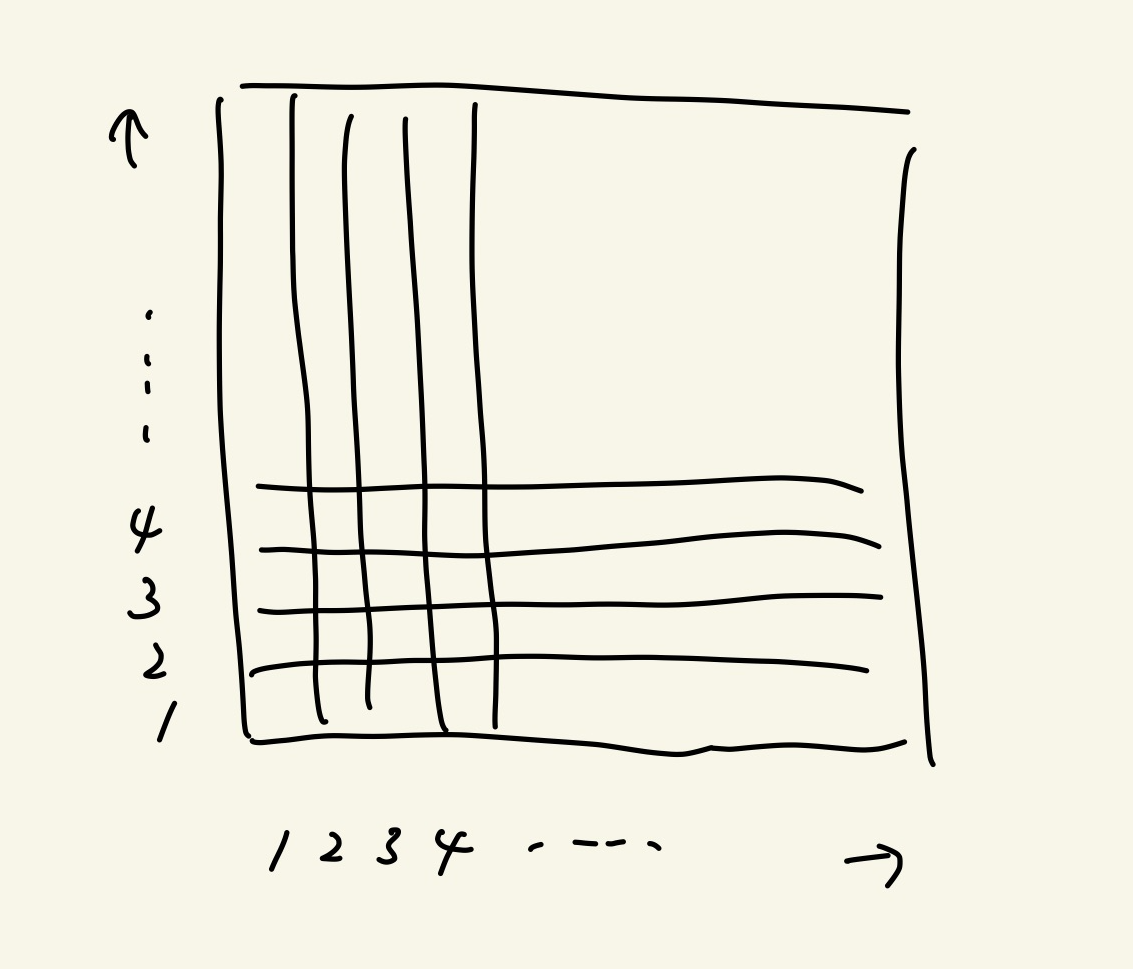
「人Aと人Bの関係」なので2次元をイメージします。

「人5と人3の関係」は、「人3と人5の関係」のように、必ず小さい値から使うように変換すると、使うデータは約半分になります。次のように左上だけ使います。

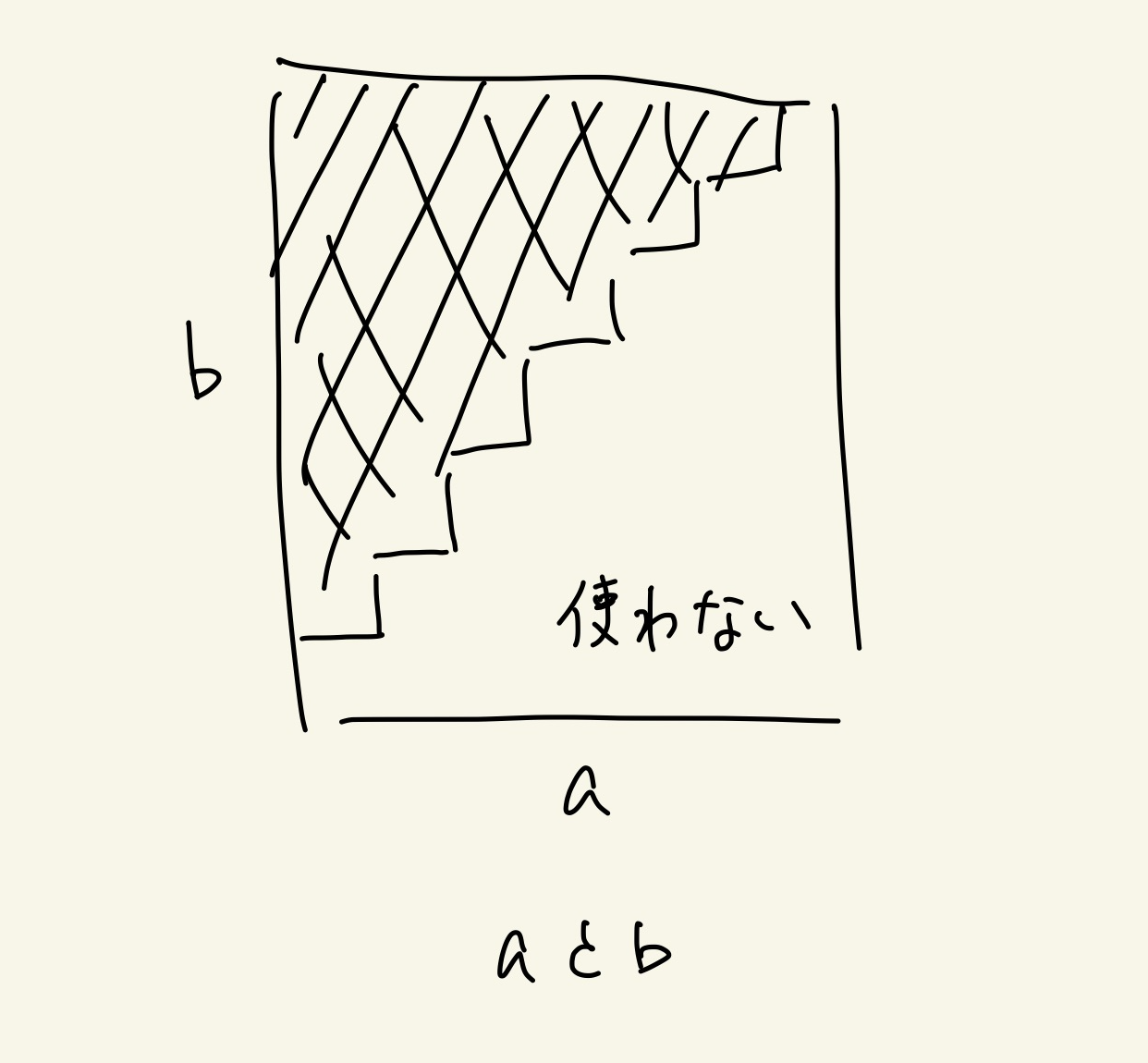
求めるものは2次元データをセグメント木化するものなので、3次元セグメント木を作成します(3次元セグメント木という名前は私が勝手に付けました)。
今まで上の積み木の方が大きいやり方で説明してきましたが、見やすくするために上下反対にして描きます。また、使わない部分を描かないでいます。

イメージ出来たので、また上の積み木の方が大きいやり方に戻します。
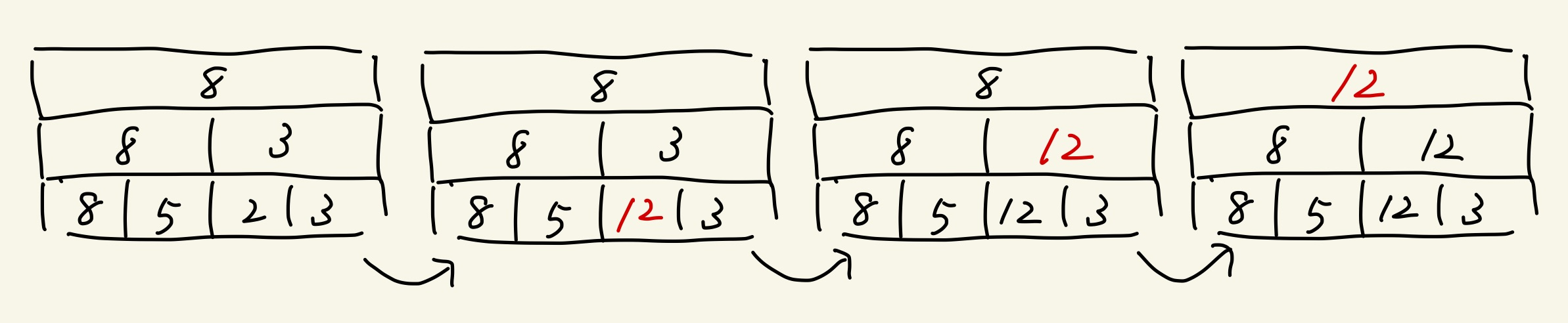
基本の動きは次のようになります。
まずは値を増加させた場合

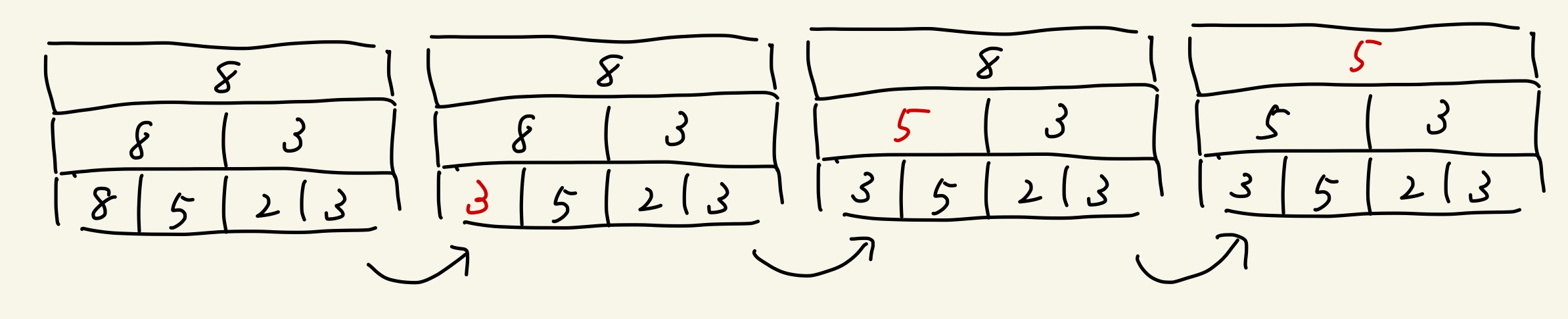
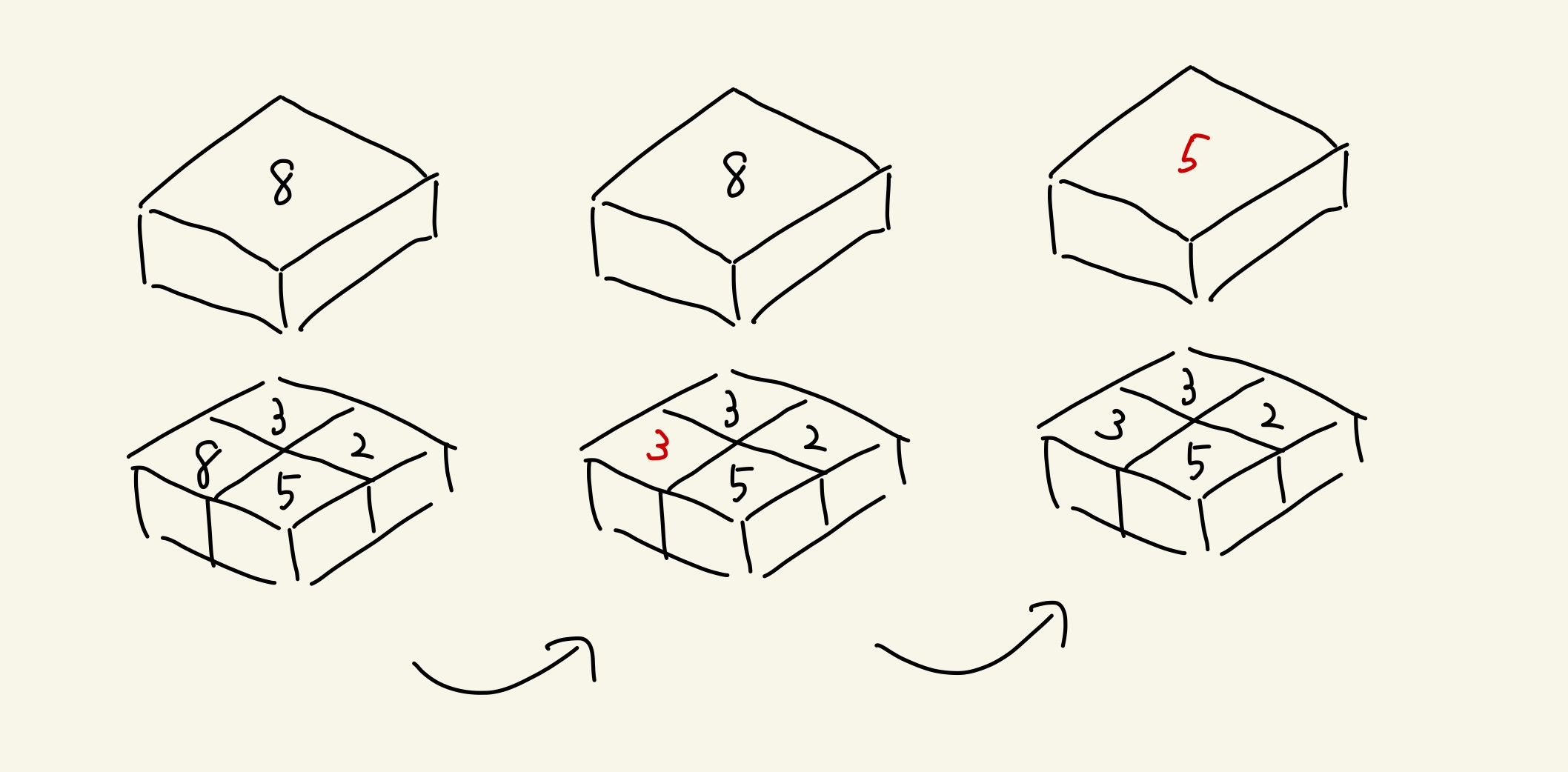
次に減少させた場合

これらの操作後に上の段へ伝えます。伝える必要がない場合はそこで伝達処理を終えます。

3次元セグメント木に与えるデータですが、人pの加入/脱退の情報が与えられたら、その他の人とpが同じになるか確認し、加入/脱退が同じになる場合は1段目の該当する箇所を0にして減少の処理を行い、加入/脱退が異なる場合は値を入力し増加の処理をします。

この3次元セグメント木のメモリ量ですが、
人が500人なので、3次元積み木の1段目に必要なのは500x500です。2のべき乗の都合から512x512で作成します。
2段目は256x256です。
10段目で1x1になり全部で10段あります。
段ごとに違う容量のものを用意するより全部統一したほうがシンプルになるので全段512x512で作成し、使わないところは放置するようにしました。
結果、512x512x10=約2,600,00
整数データが8バイトだと約21MBとなり容量も大丈夫そうです。

計算量は
1人の加入/脱退に対して、残りの約500人との関係を書き直します。
1つの関係の書き込みで1段目から10段目まで行くと、
1人の加入/脱退に対して、5000の処理があります。
加入/脱退の総数が50000なので250000000となります。
O記法だとO(QNlogN)あるいはMを入れるならO(M+QNlogN)になりますでしょうか。

コード

Swiftで書きました。

func readInt() -> Int {
    Int(readLine()!)!
}

func readInts() -> [Int] {
    readLine()!.split(separator: " ").map { Int(String($0))! }
}

func readStrings() -> [String] {
    readLine()!.split(separator: " ").map { String($0) }
}

let nmq = readInts()
let n = nmq[0]
let m = nmq[1]
let qN = nmq[2]

var favo = [[Int]](repeating: [Int](repeating: 0, count: n + 1), count: n + 1)

for _ in 1...m {
    let d = readInts()
    favo[d[0]][d[1]] = d[2]
}

var size = 1
var floors = 1
while size < n + 1 {
    size *= 2
    floors += 1
}

var st = [Int](repeating: 0, count: size * size * floors)
var joined = [Bool](repeating: false, count: n + 1)

for _ in 1...qN {
    let d = readStrings()
    let op = d[0]
    let p = Int(d[1])!
    for o in 1...n {
        if o == p {
            continue
        }
        let minP = min(o, p)
        let maxP = max(o, p)
        switch (op, joined[o]) {
            case ("+", false), ("-", true):
                if favo[minP][maxP] != 0 {
                    plus(floor: 0, p1: minP, p2: maxP, v: favo[minP][maxP])
                }
            case ("+", true), ("-", false):
                if st[minP + maxP * size] != 0 {
                    minus(floor: 0, p1: minP, p2: maxP, v: 0)
                }
            default:
                break
        }
    }
    
    print(st[size * size * (floors - 1)])
    if op == "+" {
        joined[p] = true
    }
    if op == "-" {
        joined[p] = false
    }
}

func plus(floor f: Int, p1: Int, p2: Int, v: Int) {
    let base = size * size * f
    st[base + p1 + p2 * size] = v
    if f == floors - 1 {
        return
    }
    if st[base + size * size + p1 / 2 + p2 / 2 * size] < v {
        plus(floor: f + 1, p1: p1 / 2, p2: p2 / 2, v: v)
    } 
}

func minus(floor f: Int, p1: Int, p2: Int, v: Int) {
    let base = size * size * f
    st[base + p1 + p2 * size] = v
    if f == floors - 1 {
        return
    }
    let x = p1 / 2 * 2
    let y = p2 / 2 * 2
    let maxV = max(st[base + x + y * size], 
                   st[base + x + 1 + y * size], 
                   st[base + x + (y + 1) * size], 
                   st[base + x + 1 + (y + 1) * size])
    if st[base + size * size + p1 / 2 + p2 / 2 * size] > maxV {
        minus(floor: f + 1, p1: p1 / 2, p2: p2 / 2, v: maxV)
    } 
}