SwiftのFloat系の演算で、いつのまにか余り演算子の%が使えなくなりました。使おうとすると次のエラーが出ます。
'%' is unavailable: For floating point numbers use truncatingRemainder instead
'%' は使えません。小数はtruncatingRemainderを代わりに使います。
ということで、%の代わりのメソッドを使います。エラーメッセージにはひとつしか書いてませんが、代わりのメソッドは次の2つあります。
- truncatingRemainder メソッド
- remainder メソッド
そのまとめです。
truncatingRemainder メソッド
public func truncatingRemainder(dividingBy other: Self) -> Self
従来の%に変わるものです。どんどん削っていって最後に残ったものと解釈できます。だるま落とし方式です。
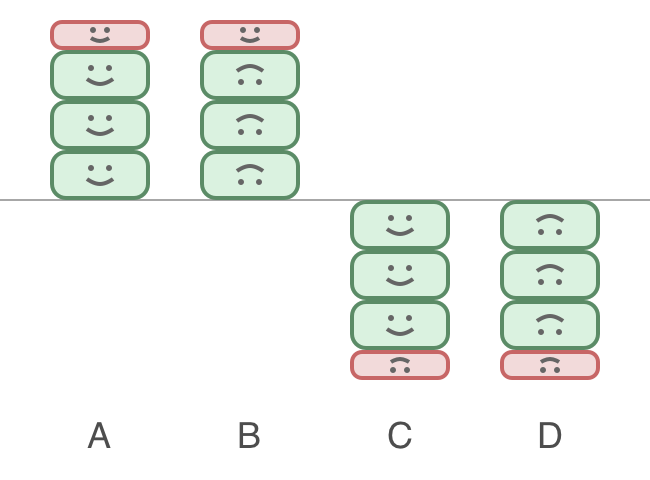
Aの例 : 18.0を5.0で割った余りは3.0
Bの例 : 18.0を-5.0で割った余りは3.0
Cの例 : -18.0を5.0で割った余りは-3.0
Dの例 : -18.0を-5.0で割った余りは-3.0
実装と実行結果はこのようになります。
18.0.truncatingRemainder(dividingBy: 5.0) //3.0
18.0.truncatingRemainder(dividingBy: -5.0) //3.0
-18.0.truncatingRemainder(dividingBy: 5.0) //-3.0
-18.0.truncatingRemainder(dividingBy: -5.0) //-3.0
【語句】truncate …の頭部[尾部]を切る
remainder メソッド
public func remainder(dividingBy rhs: Self) -> Self
もうひとつのメソッドが、remainderです。数直線上に、割る数の間隔で印をつけて、割られる数に一番近い印を見つける。その印から見た割る数の位置が余りになります。
最寄駅方式です。一番近い駅から目的地までの向きと距離、と解釈できます。
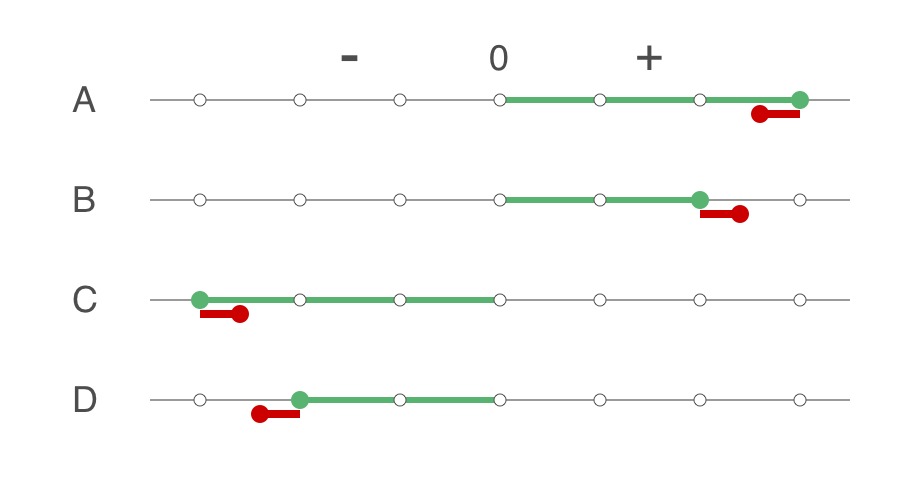
赤丸が割られる数です。
Aの例 : 13.0を5.0で割った余りは-2.0
Bの例 : 12.0を5.0で割った余りは2.0
Cの例 : -13.0を5.0で割った余りは2.0
Dの例 : -12.0を5.0で割った余りは-2.0
実装と実行結果はこのようになります。
13.0.remainder(dividingBy: 5.0) //-2.0
12.0.remainder(dividingBy: 5.0) //2.0
-13.0.remainder(dividingBy: 5.0) //2.0
-12.0.remainder(dividingBy: 5.0) //-2.0
割る数の正負が反対になっても最寄駅は変わりません。結果も同じです。
13.0.remainder(dividingBy: -5.0) //-2.0
12.0.remainder(dividingBy: -5.0) //2.0
-13.0.remainder(dividingBy: -5.0) //2.0
-12.0.remainder(dividingBy: -5.0) //-2.0