はじめに
迷路を作成するというQiitaの企画があったので参加します。
Qiitaの企画
https://qiita.com/official-events/55631b864217a4df857a
この企画は、プログラムを使ってできるだけ「良い」迷路を作るものです。良いの基準は自分で決めてよいそうです。良い迷路になるようにソース上でいろいろな工夫をしていきます。言語はSwiftを使用します。
作成する迷路について
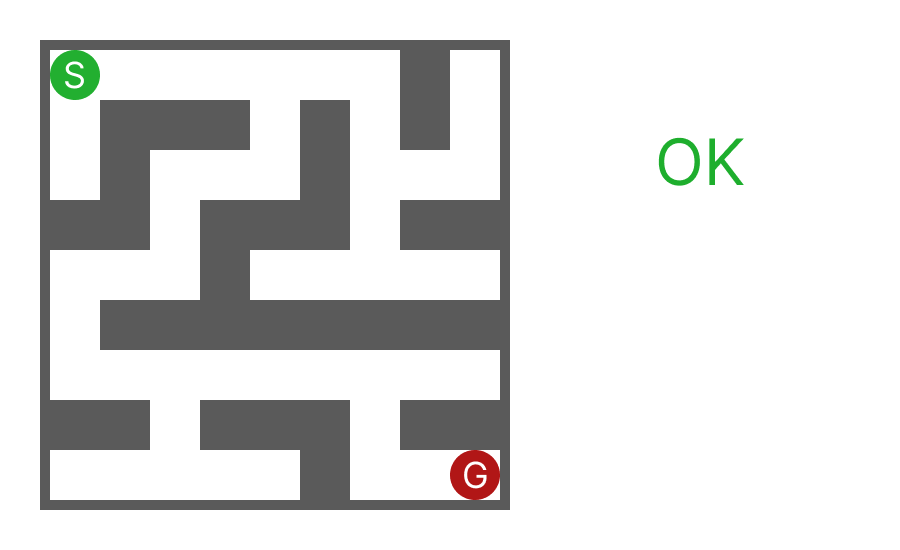
- 長方形で、左上がスタート、右下がゴール
- 大きさは縦横ともに7から30程度(壁の厚さも1と数える)
- 正解の経路は一つ
- ループ(同じところをぐるぐる回る)なし
- すべて通路になっている2x2のエリアは存在しない
- すべて壁になっている2x2のエリアは存在しない
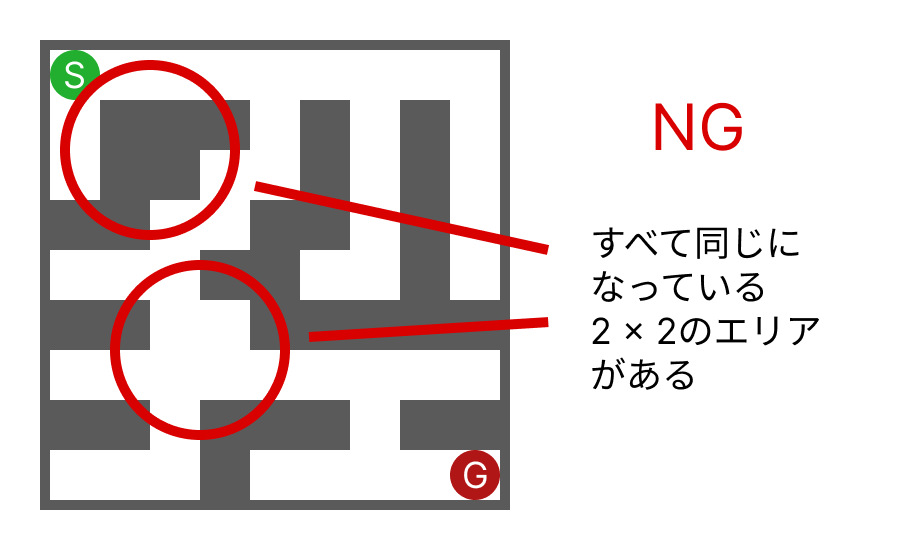
すべて通路(or壁)になっている2x2のエリアは無駄な感じがするのでやめます。
迷路作りの概要
- 乱数を利用して候補となる迷路を作成する
- 作成した候補を判定する
1と2を繰り返して良い迷路を更新していきます。
候補を作成する
構造
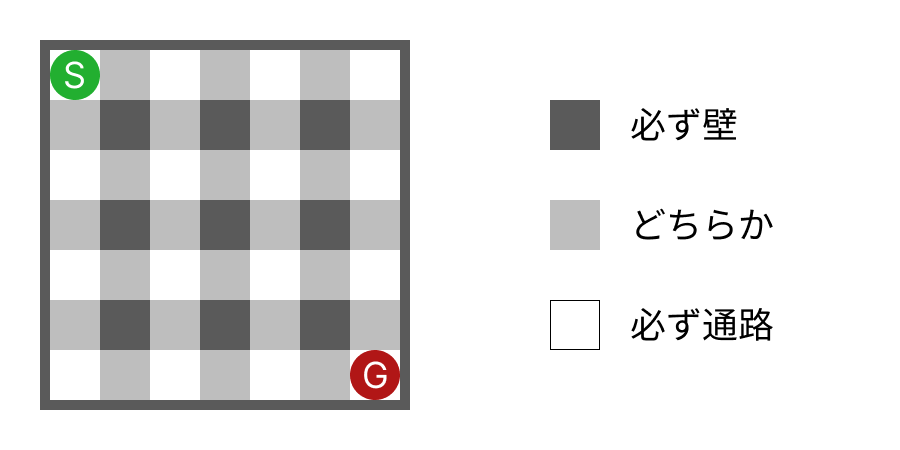
マスはその位置によって「必ず壁」「必ず通路」「どちらか」の3つに分かれます。その配置は次のようになります。
迷路の候補を作るときは、この「どちらか」のマスを通路か壁に決定していきます。完成時には「必ず通路」がすべてつながります。
上の図でわかるように縦と横のサイズは奇数になります。
このチェック模様のやり方をすると「全部壁(or通路)となる2x2のエリアは存在しない」という迷路の条件を満たします。
通路の呼び方について
候補はスタートからどんどん伸びていくように作成します。このとき、通路には
- スタートとつながっている通路
- つながっていない通路(必ず通路になるマスだがまだスタートとつながっていない)
があります。
この記事ではその2つを区別して言いたい場面で
- スタートとつながっている通路を「確定した通路」
- スタートとつながっていない通路を「未確定通路」
候補作成の基本方針
候補作成のやり方は
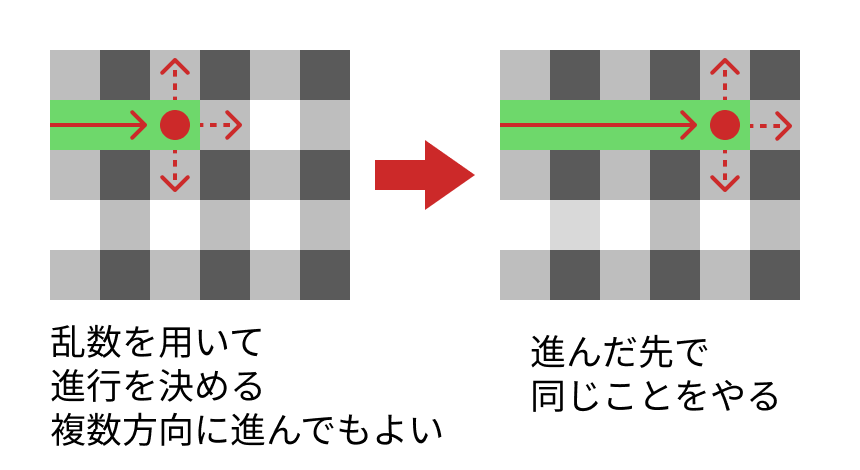
スタートから始めて、必ず通路になるマス上でどの方向に通路を伸ばすか(あるいは伸ばさないか)を乱数で決定し、進むならその方向に2つ進んで同じことする。必ず通路になるマスが全部つながるまでこれを行う。
です。
あるマスから進む方向が複数あってもかまいません。
乱数を用いるので進行が停止することがあります。停止したらどこかの場所から再開します。
細かいテクニック
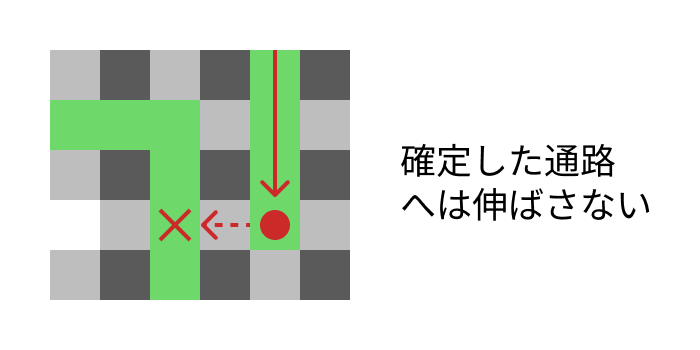
進もうとする先が確定した通路の場合、その方向には伸ばさない。伸ばしてしまうとループが発生してしまうので。
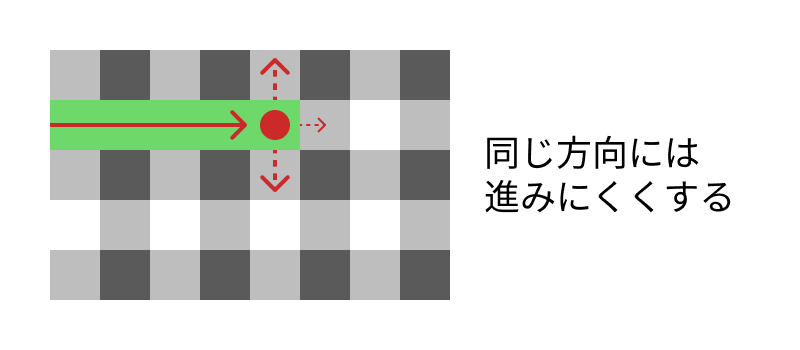
直線経路はつまらないので、直線が長くならないように、同じ方向にどれだけ連続しているかを記録して、その方向へ進む確率を小さくする。
乱数を使って判断するので途中で進行が終了してしまうことがあります。そのときは再開可能なマスを選んでそこから再開します。
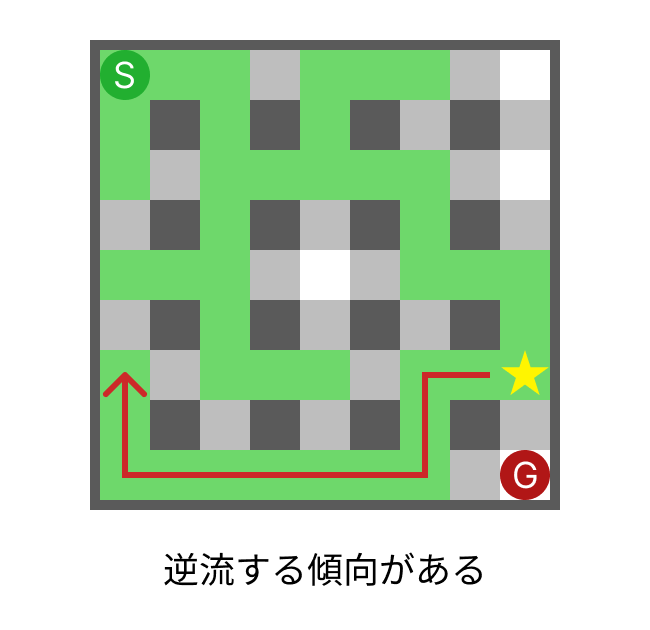
このとき、スタートに近い方のマスが選ばれるようにします。ゴールに近い方のマスを選んでしまうと次のように、ゴールに近い部分から後戻りの経路を作成する挙動が多く見られました。多くというのは私の希望と比べてです。この経路は正解ではないとすぐにバレるのでゴールに近い方のマスが選ばれる確率を少なくします。
選択するマスは、一番スタートに近いマスよりも、少しランダマイズしたほうが良かったので、ランダマイズしてスタートに近い方がだいたい選ばれるようにしています。
具体的な計算は
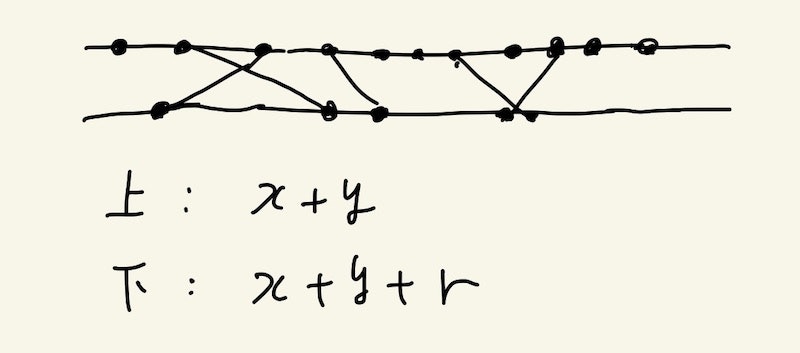
-(w + h) / 3 から (w + h) / 3 の間でランダムに値を選び r とし、x + y + r の値で最低更新の比較を行います。これをランダムに選んだ5個ほどで行い、最低の値を出したものを次のスタート地点として採用します。
候補作成のアルゴリズムまとめ
基本的に
- あるマスに到達
- x方向、y方向のどっちを先にトライするか乱数で決定
- 4方向の各方向ごとに工程4以降を実行する。
- 進む先がエリアの範囲内かチェック
- 進む先が未確定通路かチェック
- 直線チェック。直線が続いていたら進む確率が下がる
- 乱数を用いて進むかどうか判断
- 進むなら2つ進んで工程1に戻る
- 進まないなら工程3に戻る。ただしトライする方向が残っていないならそのマスは終了
- 進まなくなったらスタートに近いマスから再スタート
- 通路にすべきマスが全部つながれば(未確定通路がなくなれば)終了
です。
候補を判定する
ここから候補の判定を行います。いくつかの判定項目で点数をつけた後、掛け合わせて総合点を出します。
判定の項目
- 正解経路の長さ
- 正解経路の曲がる数
- 正解経路上の分岐の数
- 不正解経路の複雑さ
正解経路の長さ
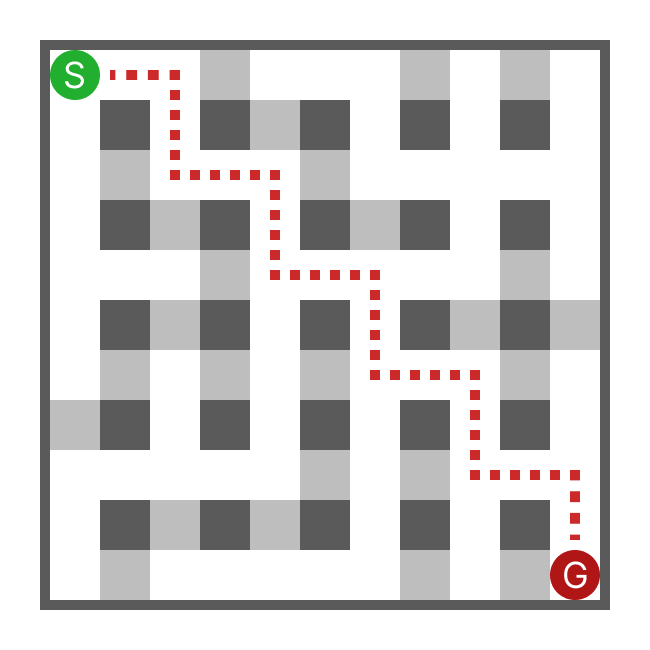
次のような迷路は良くない迷路だと思います。
このような迷路は迷路をやった感じがしません。これを回避するために「どれだけゴールから遠い方向(つまり上か左)に進むか」を判定にいれます。これは単純に正解経路の長さで判断すればよいでしょう。
正解経路の曲がる数
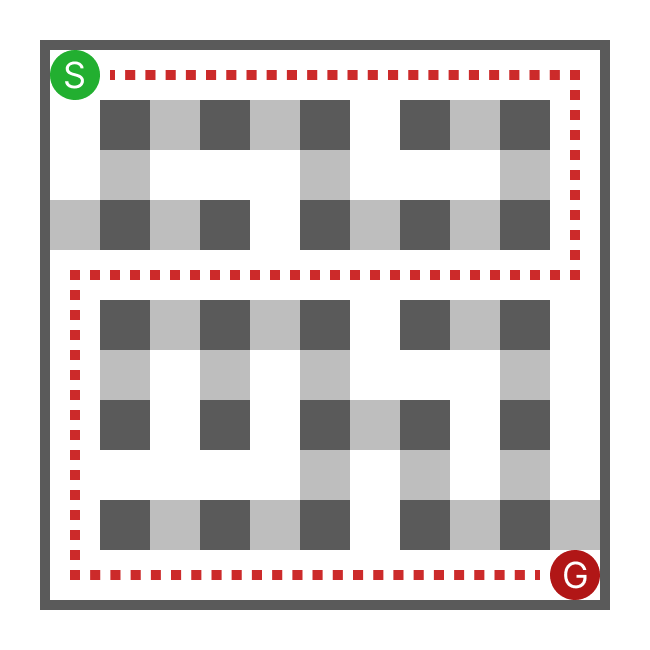
次のような迷路も良くない迷路だと思います。
これは曲がる回数が少なすぎます。これを回避するために、正解経路の曲がる数も判定に入れます。これは次のように連続する3マスの1番目と3番目の位置で判断すればよいでしょう。
1と2は横に2つ離れているので曲がってない。
2と3は縦も横も2つ離れていないので曲がっている。
3と4は縦に2つ離れているので曲がってない。
正解経路上の分岐の数
上の2つに比べて分かりにくいのですが、次のような迷路も良くない迷路だと思います。
スタートからゴールまで分岐が1回しかありません。その分岐で正しい方を選んだ場合、すぐにゴールにたどり着きます。この正解経路上の分岐の数も判定に入れます。
以上3つの評価の仕方
この3つの項目で大事なことは、できるだけ良いものを見つけるのことではなく、排除すべきものをしっかり排除するということです。つまり、上の方はあまり値が変わらなく、下の方を確実にバラつかせるというやり方をします。
これには次の式を利用します。
y = \frac{x}{x + 1}
これは
y = \frac{1}{x}
をx軸でひっくり返して、1足して左に1ずらしたものです。
ただ、得られたデータを直接xに入れてもだめなので、
y = \frac{x}{x+1}
のxの部分をf(x)を通すようにして
y = \frac{f(x)}{f(x)+1}
とします。
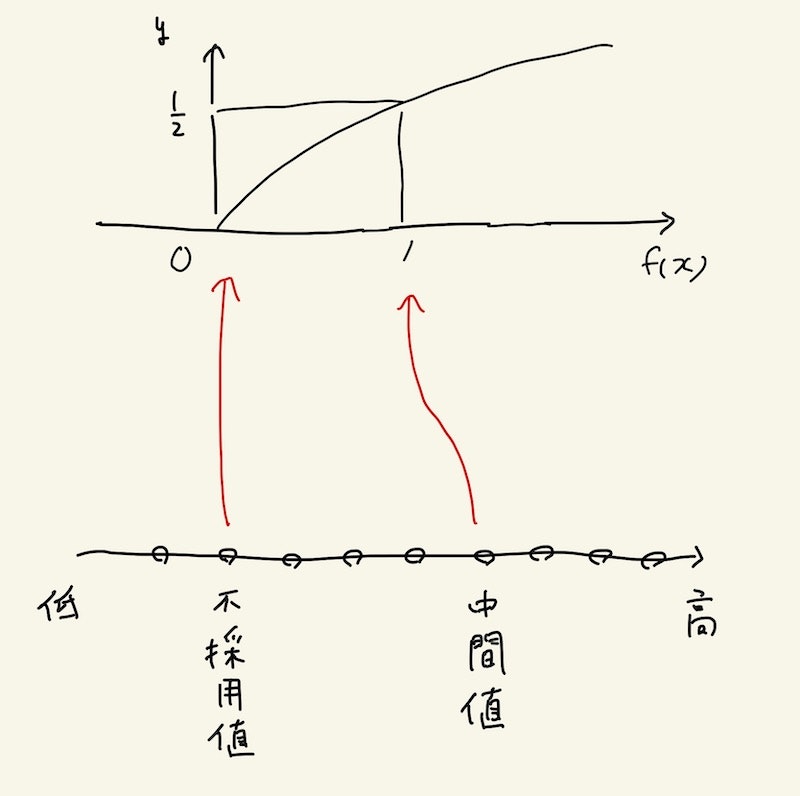
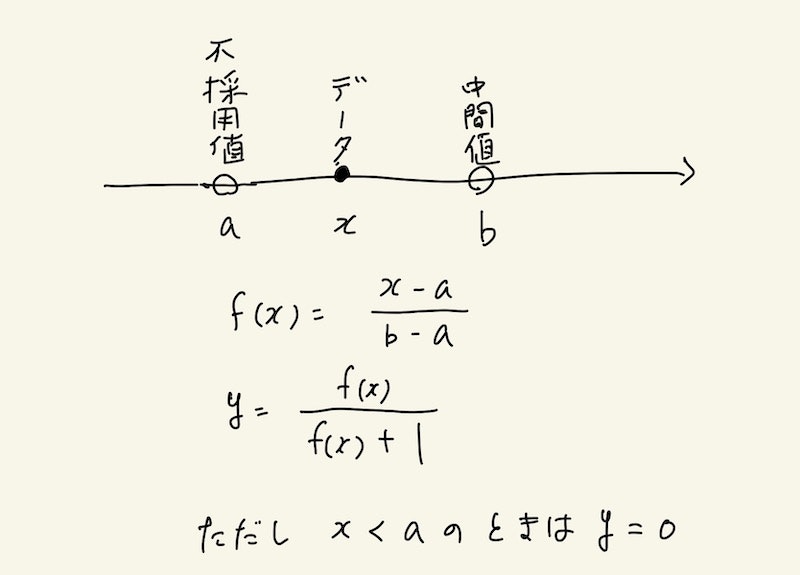
次に各項目で2つの値を決めます
- これ以下の値は採用しないという値。不採用値ということにします。
- ばらつかせる/ばらつかせないの間の値。中間値ということにします。
ここから、次のようにf(x)を調整します。
- 不採用値でf(x)が0になり、yが0になる
- 中間値でf(x)が1になり、yが1/2になる
調整
上の方も区別を明確にするように点をつけてしまうデメリット
あらためてここで上の方も区別を明確にするやり方のデメリットを説明します。
- 点が高い項目が点が低い項目を殺してしまう
- 高い点をとりやすい項目が全体を支配するため、多くの回数トライして最高のものを取り出すというやり方では出てくるものが似たものになってしまう
不正解経路の複雑さ
最後の判定項目は不正解経路の複雑さです。
不正解経路を不正解だと判断していくことが迷路の醍醐味です。そのためこの不正解経路も数値化します。基本的には経路の長さで決まりますが、分岐があればその分ボーナスが掛けられる仕様です。
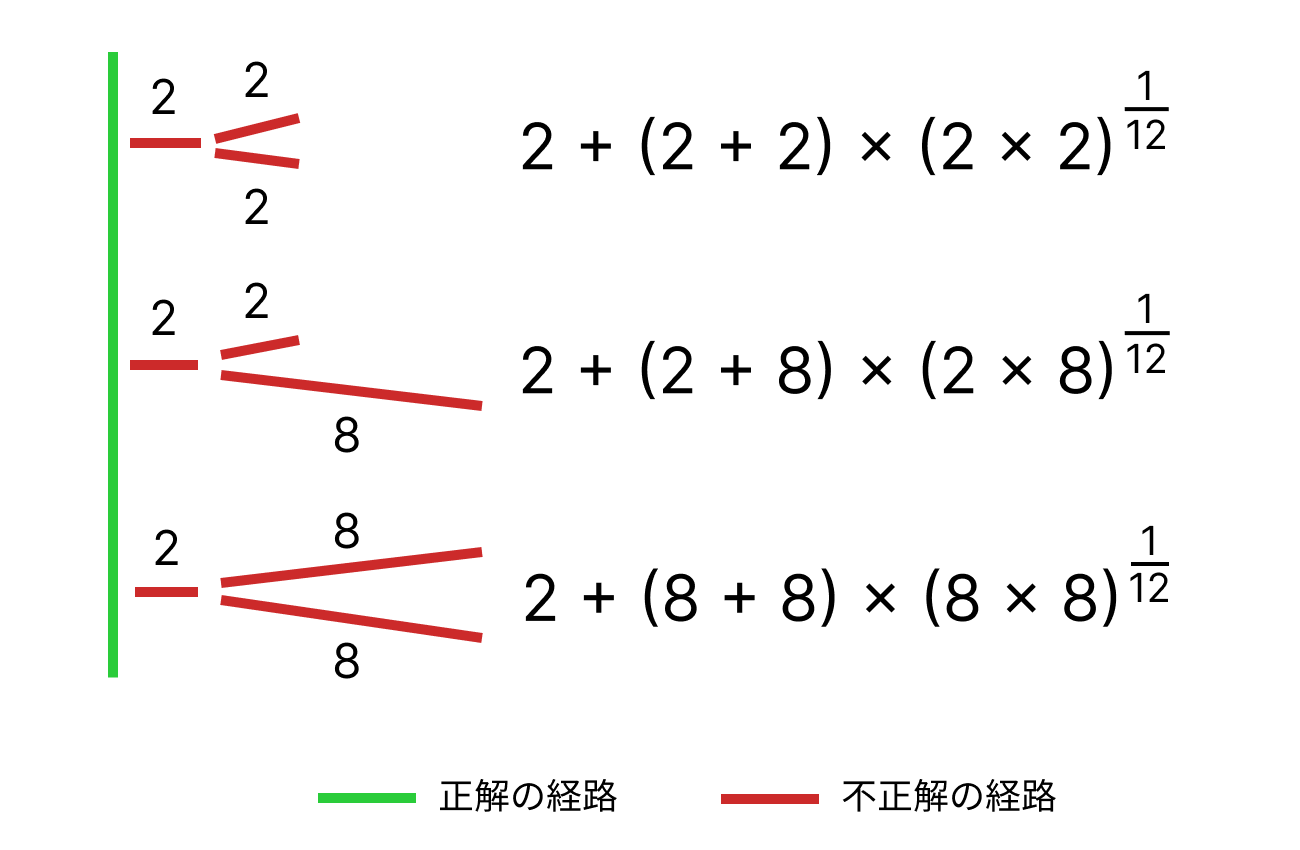
次のようにします。
分岐によって2と2に別れた場合、2+2=4という基本の値に2x2の12乗根がかけられます。値の組み合わせとその結果の一覧をこの記事の一番下に載せています。
12という値は、いくつか試して一番イメージに近いものを採用しました。感覚的な判断です。
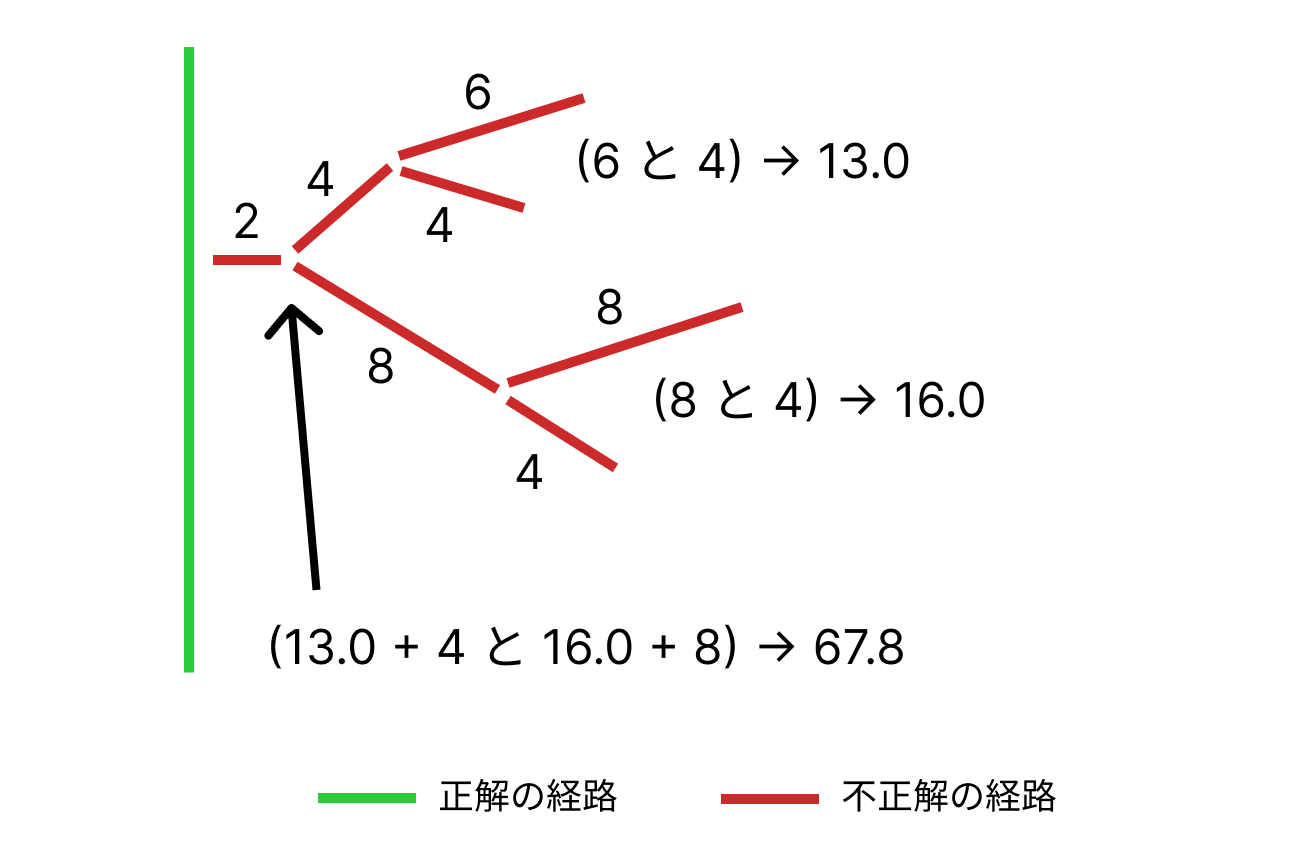
分岐が複雑になった場合は、先端側の分岐の計算結果を根本側の分岐の計算に使います。
3つに分かれているときの計算はこのようになります。
指数の値は2分岐と3分岐で同じ値を採用しました。
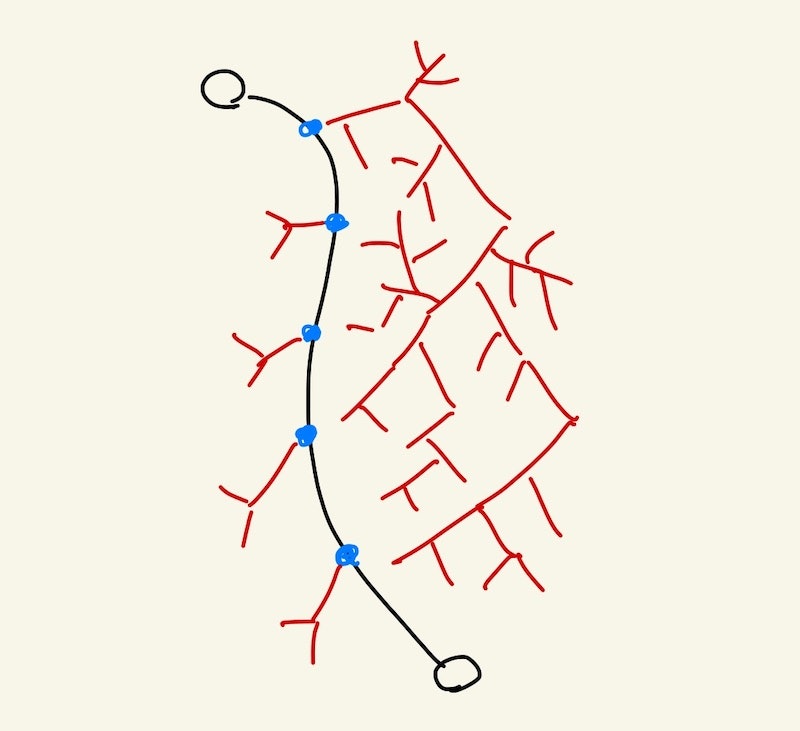
正解経路から生えているひとつの不正解経路の複雑さの求め方は以上ですが、さらに正解経路のどの部分から生えているかも考慮します。スタートに近いところから生えている方が高い点になります。ゴールに近いところは正解経路が見えやすく、不正解経路はバレやすいので。
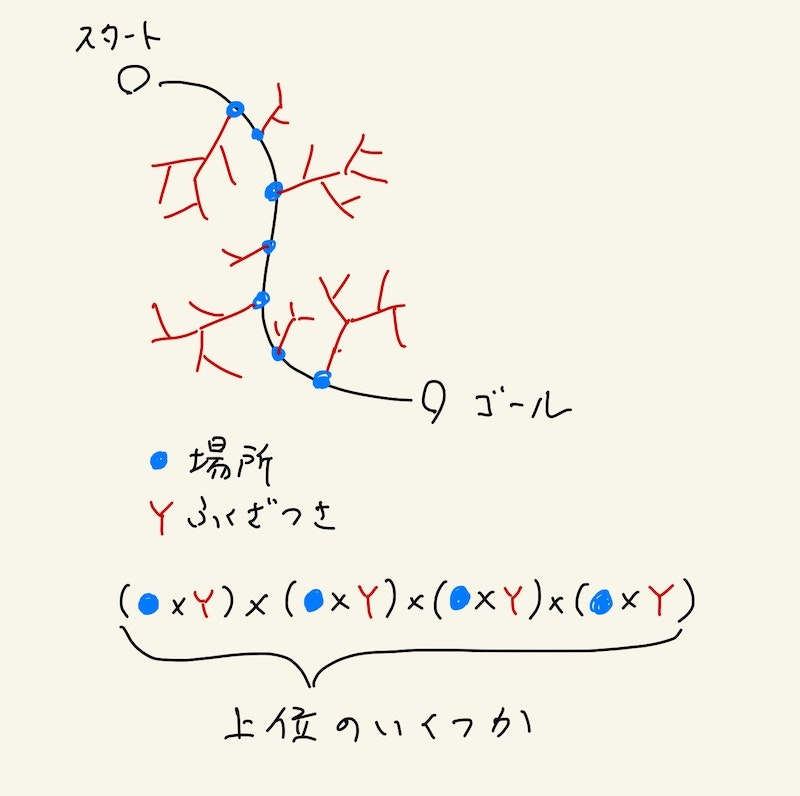
ひとつの不正解経路に対して
- 不正解経路の複雑さ
- 正解経路のどの部分から生えているか
の2つの値が求まったらかけた値を求めます。
正解経路から生えている不正解経路は複数あり、それらの値の上位のいくつかをかけます。
上位のいくつかけるかは、次のうちの最低を採用する仕様にしました。
- 不正解経路の数
- (w + h) / 6
- 8
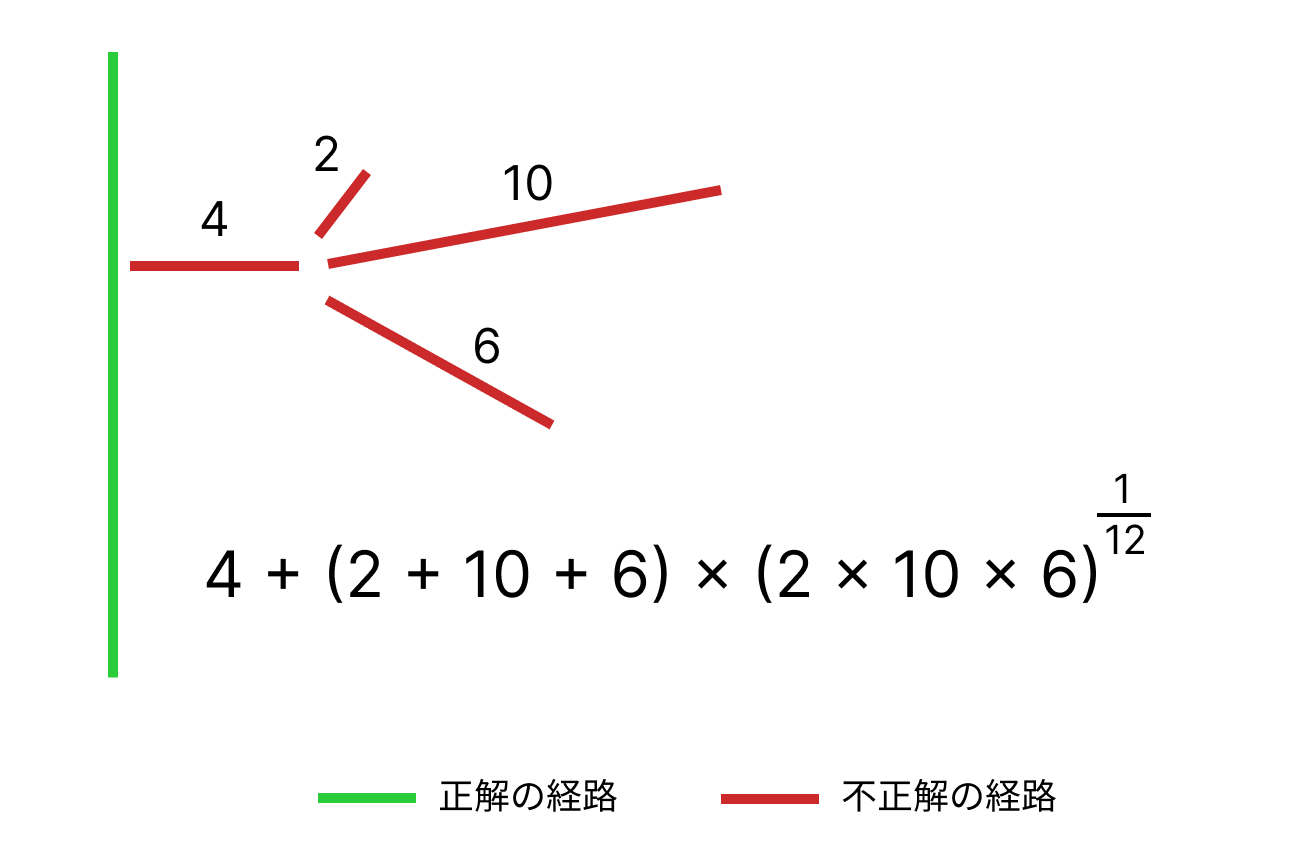
足す方法もありましたが、次の絵のように大きいものがひとつだけと細かいものが複数というパターンのときに、高い値を出してしまうのでやめました。
これは最初の分岐でたまたま正解を選んでしまうと簡単に終わってしまう迷路になります。また、正解経路が端っこを通るものになりやすいという症状がありました。
以上が不正解経路の判定方式ですが、この判定方式はまだ改良の余地があると感じます。
最終得点の求め方
各項目の点をかけた値を最終の得点とします。
今は、単純にかけているだけです。
各要素のバランスの取り方にも改良の余地があると思います。締切の関係で切り上げました。
何度か行って一番いい候補を採用する
迷路の縦と横の大きさによってトライ回数を設定します。
結果の例
文字が縦長なので「##」の2文字で壁1マスを表します。
######################
##ST ## ##
## ###### ## ## ##
## ## ## ##
###### ## ###### ##
## ## ## ##
## ###### ###### ##
## ## ## ##
## ########## ######
## ## GL##
######################
##############################
##ST ## ## ##
###### ###### ###### ######
## ## ## ##
###### ## ## ###### ## ##
## ## ## ## ##
## ########## ## ###### ##
## ## ## ##
########## ## ###### ######
## ## ## ##
## ###### ###### ##########
## ## ## ## ##
## ## ###### ###### ## ##
## ## ## ##GL##
##############################
######################################
##ST ## ## ## ## ##
## ## ###### ## ###### ## ## ##
## ## ## ## ## ##
## ###### ###### ## ########## ##
## ## ## ## ## ##
###### ########## ###### ###### ##
## ## ## ##
## ## ###### ## ########## ######
## ## ## ## ## ##
###### ## ## ###### ###### ######
## ## ## ## ## ##
###### ###### ## ###### ##########
## ## ## ## ## ##
## ############## ## ###### ## ##
## ## ## ##
## ## ## ## ###### ########## ##
## ## ## ## ## ##GL##
######################################
##############################################
##ST## ## ## ## ## ##
## ## ########## ## ## ###### ## ## ##
## ## ## ## ## ##
###### ## ## ############## ## ###### ##
## ## ## ## ## ##
## ## ###### ###### ## ############## ##
## ## ## ## ## ## ##
## ## ## ###### ########## ## ## ######
## ## ## ## ## ## ##
########## ###### ## ## ## ###### ## ##
## ## ## ## ## ## ## ## ##
## ## ########################## ###### ##
## ## ## ## ## ##
## ###### ## ########## ## ## ## ######
## ## ## ## ## ## ##
###### ## ## ## ########## ###### ## ##
## ## ## ## ## ## ## ##
## ########## ## ## ## ## ###### ## ##
## ## ## ## ## ## ## ##
## ###### ## ## ## ###### ########## ##
## ## ## ## ## ## ##GL##
##############################################
######################################################
##ST ## ## ## ## ## ##
## ###### ## ## ###### ## ###### ## ##########
## ## ## ## ## ## ## ##
## ## ## ###### ## ## ## ############## ## ##
## ## ## ## ## ## ## ##
###### ###### ###### ########## ############## ##
## ## ## ## ## ## ##
########## ############## ## ###### ###### ## ##
## ## ## ## ## ## ##
## ## ########## ############## ## ## ## ######
## ## ## ## ## ## ##
###### ## ## ###### ## ## ########## ###### ##
## ## ## ## ## ## ## ## ##
## ## ############## ## ###### ## ## ##########
## ## ## ## ## ## ##
########## ###### ## ## ## ## ########## ######
## ## ## ## ## ## ## ## ##
###### ###### ## ############## ## ###### ## ##
## ## ## ## ## ## ## ##
## ## ## ############## ## ###### ########## ##
## ## ## ## ## ## ## ##
## ###### ########## ## ###### ########## ######
## ## ## ## ## ## ##
###### ###### ## ## ## ## ########## ###### ##
## ## ## ## ## ##GL##
######################################################
##############################################################
##ST ## ## ## ## ## ## ##
###### ########## ## ## ## ## ## ########## ## ######
## ## ## ## ## ## ## ##
###### ## ## ###### ###### ## ###### ##################
## ## ## ## ## ## ## ##
## ###### ############## ## ## ## ## ## ###### ## ##
## ## ## ## ## ## ## ##
############## ## ################## ###### ## ## ######
## ## ## ## ## ## ## ## ##
## ## ## ############## ## ########## ## ########## ##
## ## ## ## ## ## ## ##
###### ###### ########## ## ## ## ########## ##########
## ## ## ## ## ## ## ## ##
## ## ## ###### ############## ## ###### ###### ## ##
## ## ## ## ## ## ## ## ## ## ##
########## ## ## ## ###### ########## ## ## ##########
## ## ## ## ## ## ## ## ##
## ## ###### ###### ## ## ## ## ## ############## ##
## ## ## ## ## ## ## ## ##
## ########## ########## ###### ## ########## ## ## ##
## ## ## ## ## ## ## ## ## ##
###### ########## ## ################## ## ## ## ######
## ## ## ## ## ## ## ##
## ###### ########## ## ## ###### ###### ########## ##
## ## ## ## ## ## ## ##
###### ###### ###### ###### ## ## ## ########## ## ##
## ## ## ## ## ## ## ## ##
###### ########## ###### ########## ## ## ## ## ## ##
## ## ## ## ## ## ## ##GL##
##############################################################
######################################################################
##ST## ## ## ## ## ## ## ## ## ##
## ## ###### ## ###### ###### ## ## ## ###### ###### ## ##
## ## ## ## ## ## ## ##
## ## ## ## ## ## ###### ## ## ###### ########## ###### ##
## ## ## ## ## ## ## ## ## ## ## ##
## ## ############## ## ## ########## ########## ## ## ######
## ## ## ## ## ## ## ## ## ## ##
########## ## ###### ## ###### ## ########## ## ########## ##
## ## ## ## ## ## ## ##
## ## ########## ########## ###### ###### ## ## ###### ## ##
## ## ## ## ## ## ## ## ##
## ###### ########## ## ############## ###### ###### ##########
## ## ## ## ## ## ## ## ##
## ########## ###### ###### ###### ###### ################## ##
## ## ## ## ## ## ## ## ##
###### ## ############## ## ## ## ## ###### ## ## ## ## ##
## ## ## ## ## ## ## ## ## ## ##
## ############## ###################### ###### ## ###### ######
## ## ## ## ## ## ## ## ## ##
###### ############## ## ## ## ########## ########## ###### ##
## ## ## ## ## ## ## ##
########## ## ########## ###### ###### ################## ######
## ## ## ## ## ## ## ## ##
## ## ############## ## ## ###### ########## ########## ## ##
## ## ## ## ## ## ## ## ## ##
## ###### ## ## ## ########## ###### ## ## ## ## ###### ##
## ## ## ## ## ## ## ## ##
###### ## ## ## ###### ############## ## ###### ## ## ######
## ## ## ## ## ## ## ## ## ## ## ## ##
## ################## ############## ###### ## ############## ##
## ## ## ## ## ##
###### ## ## ## ###### ## ###### ## ###### ########## ## ##
## ## ## ## ## ## ## ## ## ##GL##
######################################################################
ソースコード
ソースコードのいじれるところ
迷路のサイズ
var w = 15
var h = 15
ただし、この変数に値を設定しているところが別(宣言時ではない)にあればそこで設定を行う
道を開通する確率
進める方向に進むかどうか
let seed = 0.5
不採用値/中間値
点数付けの際の
- 不採用値
- 中間値
var valueSouece = [
[answerLength, 1.1, 1.3, 0.0],
[turnCount, 0.1, 0.3, 0.0],
[choiceCount, 0.1, 0.25, 0.0],
]
横に並んだ4つの値は、処理前、不採用値、中間値、処理後を入れる用、です。2番目の不採用値と3番目の中間値をいじれます。
不正解経路の分岐ボーナス
let branchBonus = 1.0 / 12.0
分岐のボーナスを大きくしたいなら、1.0 / 8.0 のようにしてください。
分岐のボーナスを小さくしたいなら、1.0 / 16.0 のようにしてください。
さいごに
最終結果だけ書いているのでシンプルに見えますが、試行錯誤を含めるとやったことはこの3倍くらいありました。
ただ、この記事に挙げたものも、無駄な部分がないとは言いきれません。
まだ、手動作成に勝ってると言い難い実感です。
付録 - 分岐の計算式 12乗根をかける効果について
for i in stride(from: 2, through: 20, by: 2) {
for j in stride(from: i, through: 20, by: 2) {
print(i, j, i + j, terminator: " ")
print(String(format: "%.2f", Double(i + j) * pow(Double(i * j), 1.0 / 12.0)))
}
}
分岐ボーナスは1/12
左から、分岐Aの値、分岐Bの値、A+Bの値、ボーナス込みの値
2 2 4 4.49
2 4 6 7.14
2 6 8 9.84
2 8 10 12.60
2 10 12 15.40
2 12 14 18.25
2 14 16 21.12
2 16 18 24.03
2 18 20 26.96
2 20 22 29.92
4 4 8 10.08
4 6 10 13.03
4 8 12 16.02
4 10 14 19.04
4 12 16 22.09
4 14 18 25.17
4 16 20 28.28
4 18 22 31.42
4 20 24 34.58
6 6 12 16.18
6 8 14 19.33
6 10 16 22.51
6 12 18 25.71
6 14 20 28.93
6 16 22 32.18
6 18 24 35.45
6 20 26 38.75
8 8 16 22.63
8 10 18 25.93
8 12 20 29.26
8 14 22 32.60
8 16 24 35.96
8 18 26 39.34
8 20 28 42.74
10 10 20 29.36
10 12 22 32.79
10 14 24 36.23
10 16 26 39.69
10 18 28 43.16
10 20 30 46.65
12 12 24 36.31
12 14 26 39.85
12 16 28 43.39
12 18 30 46.95
12 20 32 50.52
14 14 28 43.47
14 16 30 47.10
14 18 32 50.73
14 20 34 54.38
16 16 32 50.80
16 18 34 54.50
16 20 36 58.22
18 18 36 58.28
18 20 38 62.06
20 20 40 65.90