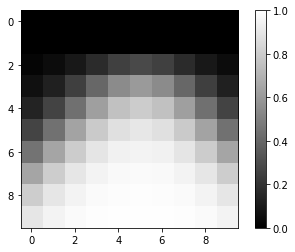ニュートラルネットワーク（重みとバイアス）応用

##ポイント
➀ニュートラルネットワークの構造
・入力ノードは二個　中間ノードは二個　出力ノードは一個
⇒中間層に必要な重みは四個　出力層に必要な重みは二個
➁重みやバイアスを変更することで、様々な出力状態を表現できるため、試してみるとよい。
➂活性化関数としては、今回シグモイド関数以外に恒等関数を用いた。
➃重みとバイアスのサイズが異なるため、演算時にはブロードキャストの知識が必要になる。
➄行列同士の計算では、dotにより実装することができる。
➅行列の初期化では、zerosやonesがよく使われる（zeros⇒0詰め行列　ones⇒1詰め行列）

##ソース

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

#x,yともに、10個のデータを準備する
X=np.arange(-1.0,1.0,0.2)
Y=np.arange(-1.0,1.0,0.2)

#10x10の0詰め行列の準備
Z=np.zeros((10,10))

#重み行列
#中間層(2x2)
w_middle=np.array([[-4.0,-4.0],
                   [4.0,-4.0]])
#出力層(2x1)
w_out=np.array([[1.0],[-1.0]])

#バイアス行列
#中間層
b_middle=np.array([3.0,-3.0])
#出力層
b_out=np.array([0])

#中間層の実装
def middle_layer(x,w,b):
  u=np.dot(x,w)+b#線形変換
  return 1/(1+np.exp(-u))#非線形変換(シグモイド関数)

#出力層の実装
def out_layer(x,w,b):
  u=np.dot(x,w)+b #線形変換
  return u #非線形変換(恒等関数）

#ニュートラルネットワークの実装
for i in range(10):
  for j in range(10):

    #入力層
    inp=np.array([X[i],Y[j]])
    #中間層
    mid=middle_layer(inp,w_middle,b_middle)
    #出力層
    out=out_layer(mid,w_out,b_out)

    #出力データの格納
    Z[j][i]=out[0]

#グリッド表示
plt.imshow(Z,"gray",vmin=0.0,vmax=1.0)
plt.colorbar()
plt.show()

##出力

##補足
・ブロードキャスト(サイズの異なる行列の演算）

a=np.array([[1,1],[1,1]])#2x2の行列
b=np.array([1,2])#一次元配列
c=np.array([[1],[2]])#2x1の行列

print(a+b)
print(a+c)
>>>
[[2 3]
 [2 3]]
[[2 2]
 [3 3]]

・行列同士の積(一般的に、MxHの行列とHxNの行列の積の結果はMxNの行列となる）

x=np.array([[2,3],[1,2],[5,6]])#3x2の行列
y=np.array([[3,3,2],[3,7,9]])#2x3の行列
print(np.dot(x,y))#3x3の行列が出力される
>>>
[[15 27 31]
 [ 9 17 20]
 [33 57 64]]

・行列の初期化(0詰め行列と1詰め行列の生成）

np.zeros((2,3))
>>>
array([[0., 0., 0.],
       [0., 0., 0.]])

np.ones((2,3))
>>>
array([[1., 1., 1.],
       [1., 1., 1.]])

##関連記事
ニュートラルネットワーク(重みとバイアス)