More than 3 years have passed since last update.

予測性と説明性を両立した一般化加法モデルとGA2M

Last updated at 2020-11-20Posted at 2019-09-24

はじめに

線形モデルの一つに一般化加法モデルが存在します。
存在は知っていましたが、今まで気にとめることはありませんでした。
先日、KDD2019においてMicrosoftのチームが、医療データにおける分析についてのセッション(参考)を行ったそうです。
そこで、医療分野で予測モデルを作成した際には、予測精度と共に説明性が求められることが多く、その時に一般化加法モデルが有用だと紹介していたそうです。
また、一般化加法モデルに交互作用項を加えたGA$^2$Mを紹介していたそうです。
非常に気になりましたので、簡単にまとめてみたいと思います。

一般化加法モデル

概要

一般化加法モデルは、次のように表現される線形モデルです。

Y = \beta_0 + \sum^M_{i=1} f_i(x_i)

一般化線形モデルでの線形予測子を、非線形な関数の和としたモデルです。
この時の非線形な関数は、局所回帰関数、平滑化スプライン、Bスプライン、自然スプライン等が用いられます。
その中でも平滑化スプラインを用いた非線形関数で構成されたGAMが多く用いられているようです。
変数が１つの時の$f(x)$を推定することを考えます。
平滑化スプライン補間では次のペナルティ付き残差平方和PRSSが最小になるような、$f(x)$を推定します。

PRSS=\sum_{i=1}^n(y_i-f(x_i))^2+\lambda \int^{\infty}_{-\infty} \{f''(x)\}^2dx

ただし、$x_1<x_2<...<x_n$あり、$f''(x)$は曲率、$\lambda$は平滑化パラメータです。
第一項は、データへの当てはまりを表現する項、第二項は曲げ弾性エネルギーと呼ばれ小さいほど曲線が滑らかになる。
$\lambda$を$\infty$に近づけると$f(x_i)$は一次関数=直線に近づきます。
逆に、$\lambda$を0に近づけると与えられた全てのデータを滑らかな曲線で表現するようになります。
つまり、過学習することになるため、最適な$\lambda$を一般化クロスバリデーションで探索する必要があります。

Rで一般化加法モデル作成

一般化加法モデルはmgcvパッケージで実装できます。
今回利用するデータは、定番のBostonデータです。
はじめに通常の線形回帰モデルを当てはめてみます。

library(tidyverse)
library(mgcv)
require(MASS)
select <- dplyr::select

lm.model <- lm(medv~tax+crim+age+ptratio+nox+ptratio+dis, data=Boston)
summary(lm.model)

> summary(lm.model)

Call:
lm(formula = medv ~ tax + crim + age + ptratio + nox + ptratio + 
    dis, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-13.111  -4.661  -1.301   2.431  32.135 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  8.609e+01  4.480e+00  19.217  < 2e-16 ***
tax          2.793e-04  3.023e-03   0.092  0.92641    
crim        -1.754e-01  4.448e-02  -3.944 9.15e-05 ***
age         -5.282e-02  1.800e-02  -2.935  0.00349 ** 
ptratio     -1.794e+00  1.669e-01 -10.751  < 2e-16 ***
nox         -3.610e+01  5.188e+00  -6.960 1.08e-11 ***
dis         -1.654e+00  2.549e-01  -6.488 2.10e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.946 on 499 degrees of freedom
Multiple R-squared:  0.4365,	Adjusted R-squared:  0.4297 
F-statistic: 64.42 on 6 and 499 DF,  p-value: < 2.2e-16

tax以外は統計的に有意な影響があるようです。
次に一般化加法モデル(gam関数)です。
基本的には、通常のlm関数の記法と同じですが、説明変数をs()で囲うことで非線形関数とすることができます。
s()で囲わないと通常の一次関数の回帰となります。

gam.model <- gam(medv~s(tax)+s(crim)+s(age)+s(ptratio)+s(nox)+s(ptratio)+s(dis), data=Boston)

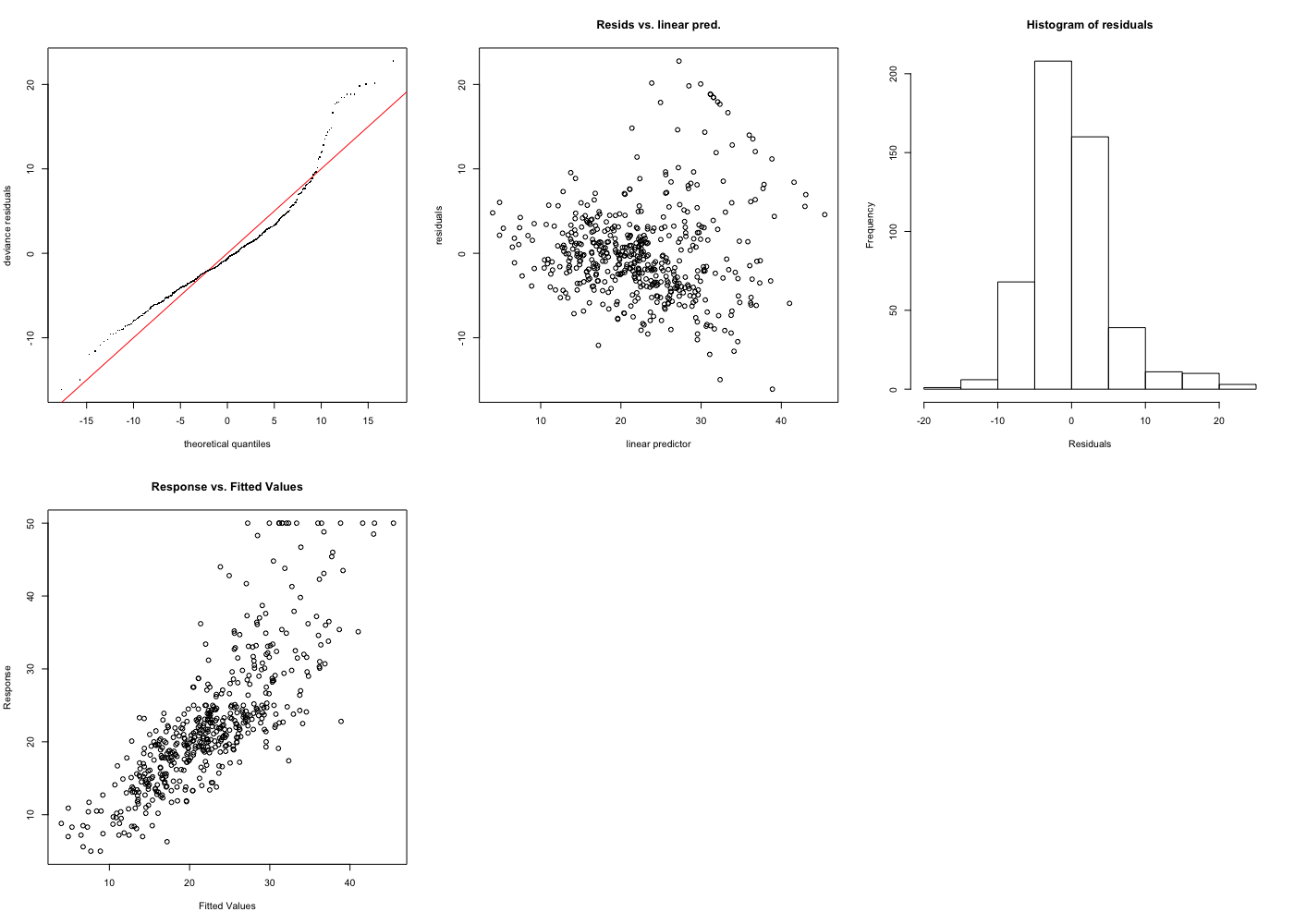
推定されたモデルを確認してみます。

> gam.check(gam.model)

Method: GCV   Optimizer: magic
Smoothing parameter selection converged after 16 iterations.
The RMS GCV score gradient at convergence was 2.019673e-06 .
The Hessian was positive definite.
Model rank =  55 / 55 

Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.

             k'  edf k-index p-value    
s(tax)     9.00 7.22    0.67  <2e-16 ***
s(crim)    9.00 3.46    0.96   0.135    
s(age)     9.00 1.00    1.04   0.830    
s(ptratio) 9.00 7.05    0.70  <2e-16 ***
s(nox)     9.00 8.75    0.67  <2e-16 ***
s(dis)     9.00 8.49    0.89   0.005 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

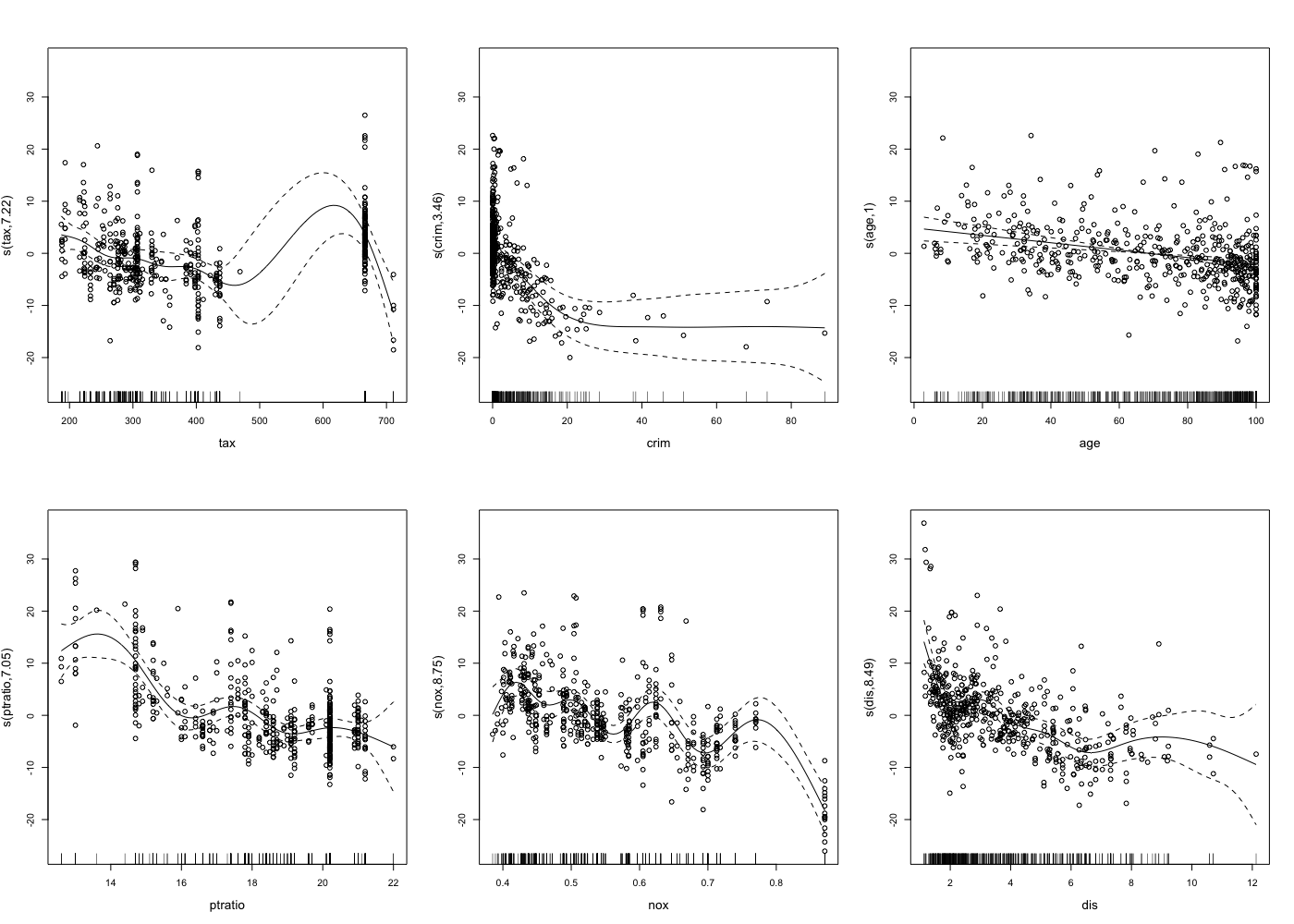
各変数における目的変数への影響の平滑化曲線を可視化してみます。

plot(gam.model, residuals=T, pch=1, se=T, cex.lab=1.3)

crimは線形モデルだと、有意な負の影響があると出ていますが、20以下だと影響が弱くなり、0付近では正の影響があると言えるようです。
disに関しても、5以下だと影響が弱くなり、0付近では正の影響があると言えるようです。
より細かい分析ができそうですね。

#交互作用を含めた一般化加法モデル

概要

交互作用を含めた一般化加法モデルは次にように表現できます。

Y = \beta_0 + \sum_{i=1} f_i(x_i)+ \sum_{i \neq j} f_{ij}(x_i, x_j)

この時の平滑化は、平滑化スプラインは利用できず、薄板平滑化スプライン(Thin plate spline法)を用いることになります。
薄板平滑化スプラインは、２変数に限らない多変量の時のスプライン補間です。
次のような$f$に関する最小化問題を解くことを考えことになります。

 \begin{aligned} \| \boldsymbol Y - \boldsymbol f \|^2 + \lambda J_{md}(f) \end{aligned}

ここで、$f$は$i$番目の要素に$f(x_i)$を持つ関数値ベクトルです。
$J_{md}(f)$は$f$の滑らかさを表現する罰則項で、次にように表現されます。

J_{md}(f) = \int \cdots \int_{\mathcal{R}^d} \sum_{\nu_1 + \cdots + \nu_d = m} \frac{m!}{ \nu_1 ! \ldots \nu_d !} \left( \frac{\partial^m f}{ \partial x_1^{\nu_1} \cdots \partial x_d^{\nu_d} } \right)^2 dx_1 \ldots dx_d

特に2変数の交互作用$m=d=2$の時は次のようになります。

J_{22}(f) = \int \int_{\mathcal{R}^2} \sum_{\nu_1 + \nu_2 = 2} \frac{2!}{ \nu_1 ! \nu_2 !} \left( \frac{\partial^2 f}{ \partial x_1^{\nu_1} \partial x_2^{\nu_2} } \right)^2 dx_1 dx_2

Rで交互作用を含めたGAM

Rで交互作用を含めたGAMを作成するためには、次のようにs()に2つの説明変数を含めれば良いです。

gam.model <- gam(medv~s(ptratio)+s(rm)+s(ptratio,rm), data=Boston)

> gam.check(gam.model)

Method: GCV   Optimizer: magic
Smoothing parameter selection converged after 58 iterations.
The RMS GCV score gradient at convergence was 0.001950721 .
The Hessian was not positive definite.
Model rank =  46 / 46 

Basis dimension (k) checking results. Low p-value (k-index<1) may
indicate that k is too low, especially if edf is close to k'.

              k'   edf k-index p-value
s(crim)     9.00  1.72    1.04    0.81
s(rm)       9.00  6.81    0.98    0.35
s(crim,rm) 27.00 27.00    1.05    0.81

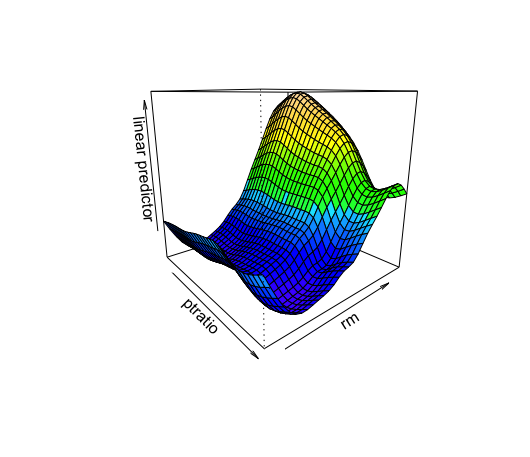
結果を３Dの可視化してみます。
パラメータにse=Tを追加すると信頼区間も図示できますが、結構見にくくなります。

vis.gam(gam.model,color="topo",theta=50)

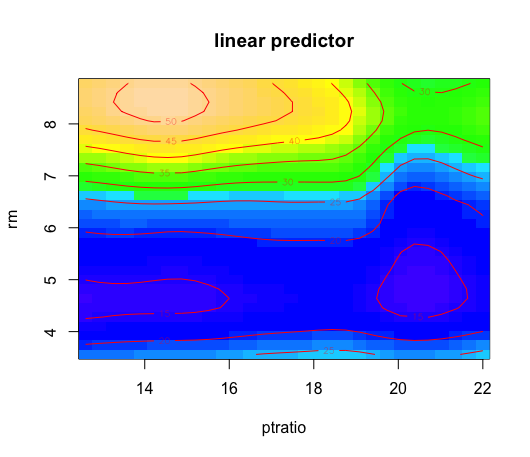
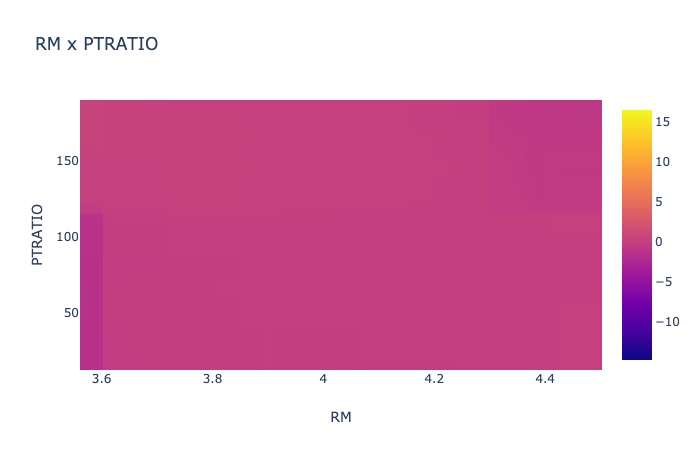
また、ヒートプロットもやってみます。

vis.gam(gam.model,color="topo",plot.type="contour")

GA2M

GA$^2$MはMicrosoftが開発しKDD2015で発表した、GAMに交互作用項を含めたモデルです。<[論文](https://www.microsoft.com/en-us/research/wp-content/uploads/2017/06/KDD2015FinalDraftIntelligibleModels4HealthCare_igt143e-caruanaA.pdf)>
正確には、単にGAMに交互作用項を入れたものではなく、GAMを拡張し高速化したExplainable Boosting Machine(EBM)です。(結果を見るに決定木ベースのモデル？)

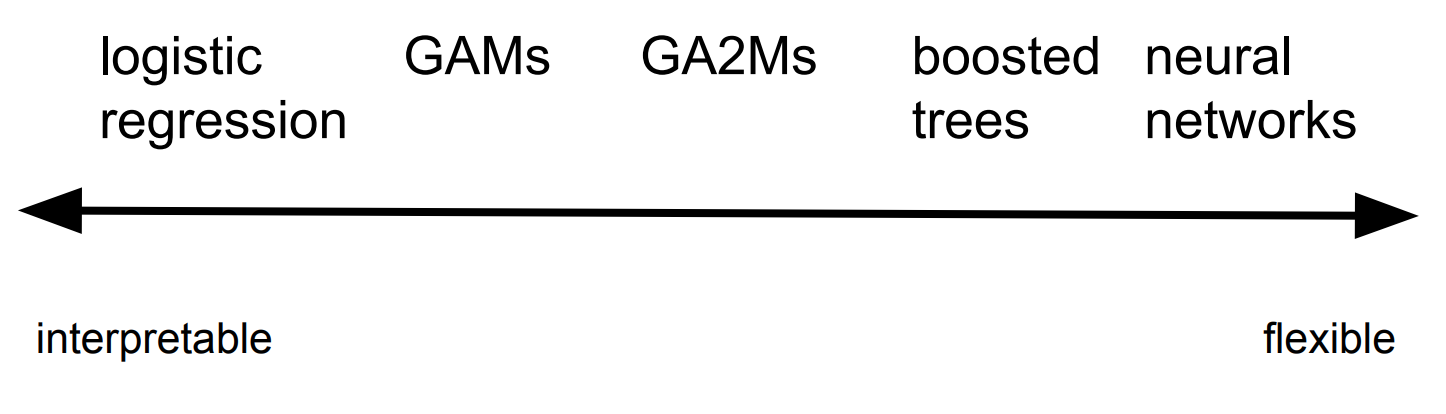
また、ロジスティック関数のような説明性とNeural Networkのような柔軟性(予測性)をそれぞれ持ち合わせたモデルであるとしています。

MSの公式は予測精度について次にような結果を示しており、データセットによってはXGBoostと同程度かそれ以上の精度が出るとしています。

Dataset/AUROC	Domain	Logistic Regression	Random Forest	XGBoost	Explainable Boosting Machine
Adult Income	Finance	.907±.003	.903±.002	.922±.002	*.928±.002*
Heart Disease	Medical	.895±.030	.890±.008	.870±.014	*.916±.010*
Breast Cancer	Medical	*.995±.005*	.992±.009	*.995±.006*	*.995±.006*
Telecom Churn	Business	.804±.015	.824±.002	.850±.006	*.851±.005*
Credit Fraud	Security	.979±.002	.950±.007	*.981±.003*	.975±.005

交互作用を含めたGAMはmgcvパッケージでも良いですが、予測タスクの場合は説明変数が多量になることが多く、交互作用を一々記述したり確認するのは困難になってくると考えられます。
このGA$^2$Mだと全ての組み合わせにおける影響の算出を行ってくれますし、ライブラリが提供するUI上で影響度が大きい交互作用の組み合わせを優先的に表示してくれます。
こちらの記事では、次にような利用時のポイントをあげています。

GAMはで十分な精度が得られるならGAMを利用する。
GAMよりもはるかに精度がある場合や、ドメインの知識から実際の相互作用があると考えられる場合、交互作用があまり複雑ではない場合、GA$^2$Mを使用する。
データについての解釈があまりない(データの癖が強い？)場合は、boosting tree（xgboostまたはlightgbm）を試す。
画像や音声、コンテキストなど、高度で複雑な相互作用がある場合、Neural Networkまたは複雑な相互作用を捉えれるモデルを利用する。

PythonでGA2M

Pythonのinterpretライブラリで実装可能です。
基本的な利用方法は、Microsoftが公開しているGithubのページに記載してあります。
簡単にモデル作成と結果表示を行ってみたいと思います。

import pandas as pd
import plotly
from interpret import show
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split

boston = load_boston()
feature_names = list(boston.feature_names)
df = pd.DataFrame(boston.data, columns=feature_names)
df["target"] = boston.target
# df = df.sample(frac=0.1, random_state=1)
train_cols = df.columns[0:-1]
label = df.columns[-1]
X = df[train_cols]
y = df[label]

seed = 1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=seed)

from interpret.glassbox import ExplainableBoostingRegressor, LinearRegression, RegressionTree

ebm = ExplainableBoostingRegressor(random_state=seed,interactions=15)
ebm.fit(X_train, y_train)   #Works on dataframes and numpy arrays

explanation = ebm.explain_global()

show(explanation)

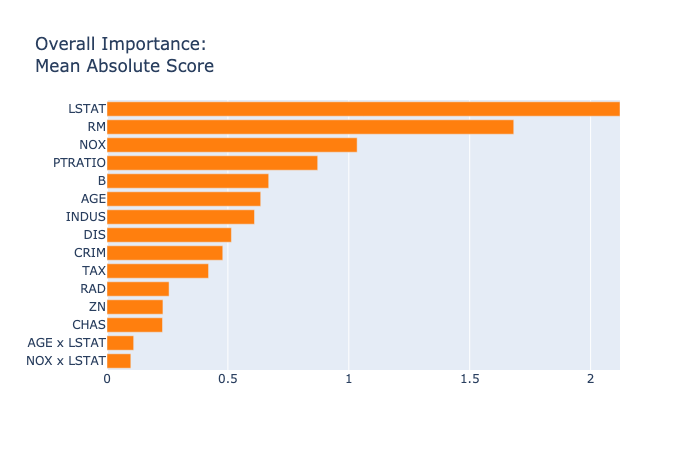
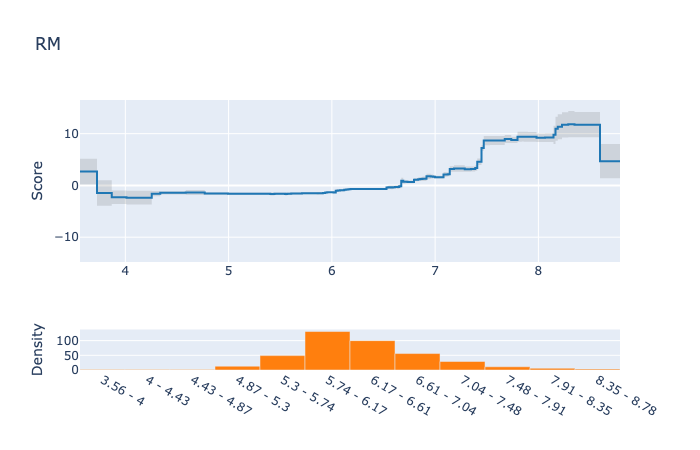
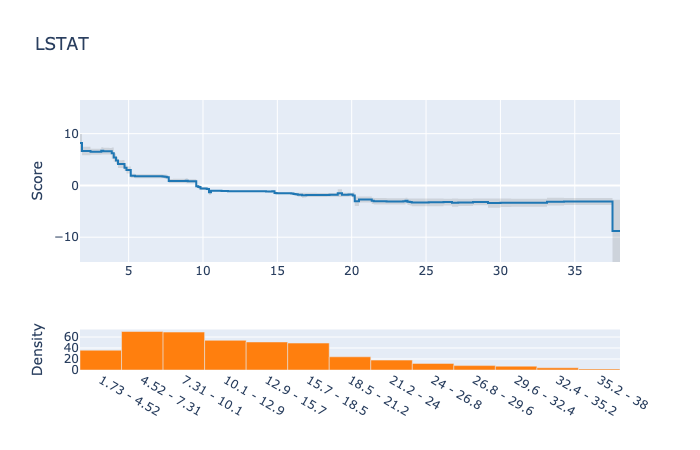
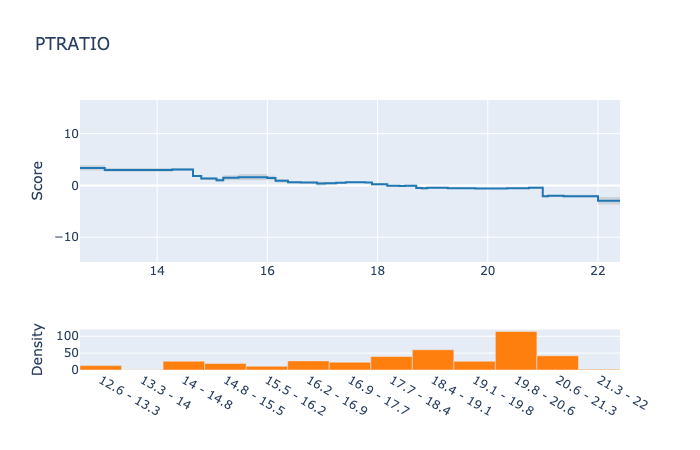
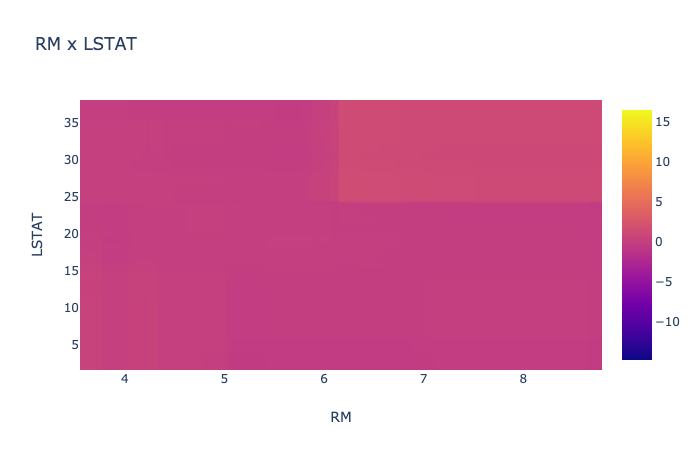
結果を表示するUIがブラウザで立ち上がります。
そこでは次にような結果が見ることができます。

今回のデータでは、目立った交互作用はありませんでしたが、結果がわかりやすいですね。
交互作用を入れたGAMは、今後色んなところで使っていきそうです。

では、以上です。

参考

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up