はじめに
前回のネットワーク指標編に引き続き、共立出版のRで学ぶデータサイエンスシリーズのネットワーク分析を読み進めていきます。
今回は検定や指数ランダムモデルについてです。
個人的にはなかな面白かったトピックでした。
igraphとggraph、tidygraphパッケージを使える所は使ってきます。
また、こちらで掲載しているコードの詳細はgithubにあげています。
※ネットワークをグラフと言ったり、ネットワークといったりしていてわかりにくいかもしれません。
ネットワークの統計的仮説検定
ネットワークでも仮説検定が行えます。
t検定等の統計的仮説検定では、分布を仮定しますが、ネットワークの密度等は次数等の条件により変化してしまうため、指標の分布は正確に得られないです。
そこで、帰無仮説に基づいてモンテカルロシミュレーションによりネットワークデータを発生させ統計量の分布を求める方法が用いられます。
QAP検定
QAP検定(Quadeatic Assignment Procedure test)は、同じノードからなる2つのネットワーク間の相関関係の有意性を判断する手法です。
あるAとBのネットワーク間の相関係数が0.7をとる場合、AとBのネットワーク関係は同じ傾向にあると言えそうです。
しかし、ネットワークサイズが小さい場合には、エッジの存在パターンはさほど多くなく、ランダムにエッジを設定したとしても、2つのネットワークは似通ったものになる可能性があります。
そこで、「Bのネットワークのエッジをランダムに設定した」という帰無仮説を設定、相関が0.7以上がどれぐらいの確率を調べ、帰無仮説が棄却されるのかを検討します。
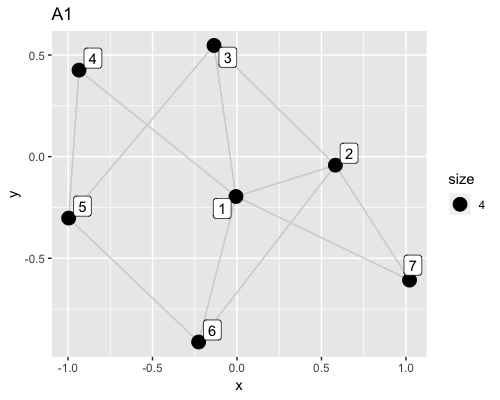
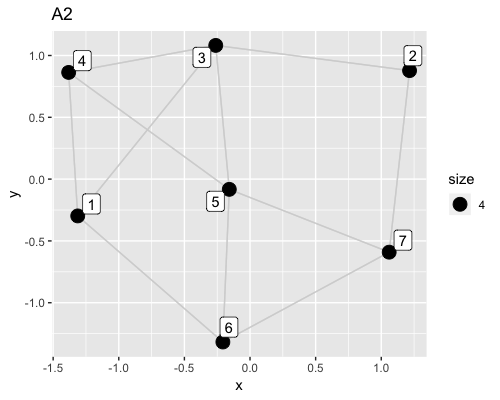
例えば、次のような7ノードからなる2つのネットワークにおいて、ノードを固定した場合のエッジのパターンは7!=5040通りあります。
そのパターン全てにおいて全て相関係数を求め、確率分布を求めれば、検定が行えます。
しかし、ノードが増えるごとにパターンが爆発的に増えていくことになり、全パターンにおける相関係数を求めることが難しくなります。
そこでノードの配置をランダムに変えるモンテカルロシミュレーションを行い、各配置における相関係数を求め、分布を近似的に求めます。
この手法がQAP検定です。
Rではsnaパッケージのqaptest関数があります。
初めにネットワークA1,A2の相関係数を確認します。
> #ネットワークスタックの作成
> gstack <- array(dim = c(2,7,7))
> gstack[1,,] <- A1
> gstack[2,,] <- A2
>
> gscor(gstack)[1,2]
[1] 0.6181818
少し高めの相関が認められそうですが、これが偶然だったかを検定します。
> qap <- qaptest(gstack, gcor, g1 = 1, g2 = 2, reps = 1000)
> summary(qap)
QAP Test Results
Estimated p-values:
p(f(perm) >= f(d)): 0.063
p(f(perm) <= f(d)): 0.998
Test Diagnostics:
Test Value (f(d)): 0.4272727
Replications: 1000
Distribution Summary:
Min: -0.5272727
1stQ: -0.1454545
Med: 0.04545455
Mean: 0.01471818
3rdQ: 0.2363636
Max: 0.6181818
2つネットワークの相関係数より大きい場合が6.3%と有意水準を5%と設定すると、帰無仮説は棄却されません。
なお、シミュレーション回数(reps引数)の設定次第で変化していきます。
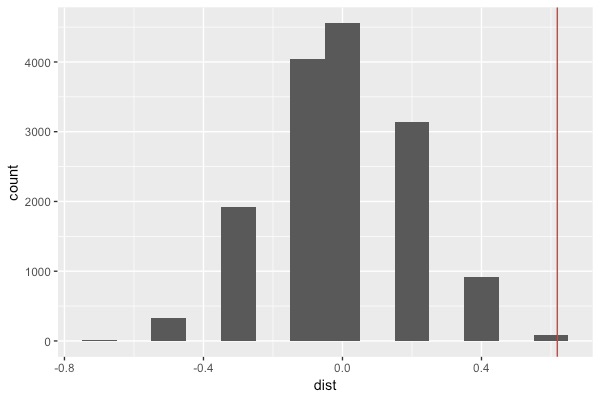
得られた分布を見てみましょう。
qap_df <- data.frame(dist = qap$dist)
gp <- ggplot(qap_df, aes(x = dist)) +
geom_histogram(binwidth = 0.1) +
geom_vline(xintercept = gscor(gstack)[1,2], colour = "red")
gp
(これで有意差が認められないのか〜 ノード数が少ないから仕方ないのか)
GUP検定
様々なネットワーク指標はノードの数や密度等の条件の影響を受けるため、ノードの数や密度等が異なる場合に指標を比べるのは難しいです。
例えば、この二つのある企業の管理職の関係性のネットワークの場合を考えていきます。
アドバイスを求めるかを表したADVICEと友人であるかを表しているFRIENDです。
<図を入れる>
この二つのネットワークの相関はあまり高くないため、類似度は低そうです。
> gcor(ADVICE, FRIEND)
[1] 0.1545855
一方で、これらのネットワークのサイズと密度で0.8といった高い値を取ることは可能でしょうか。
サイズや密度によっては、ネットワークの類似度が必然的に高くなったり、低くなったりします。
この疑問に対する解決方法として、ネットワークのサイズや密度の固定するという制約のもとで、ネットワークの指標がどの程度起こるのかを推定し、統計的有意差を検証するCUG検定(Conditional Uniform Graph test)があります。
CUG検定はQAP検定と同様に,制約のもとでモンテカルロシミュレーションを行い、指標の分布の近似を得ることにより検定を行います。
Rではcugtest関数で提供されている。
ADVICEとFRIENDにおいて、上記の相関係数は有意な値であるかを検定を行います。
> gstack <- array(dim = c(2,21,21))
> gstack[1,,] <- ADVICE
> gstack[2,,] <- FRIEND
> cug_test <- cugtest(gstack, gcor)
> summary(cug_test)
CUG Test Results
Estimated p-values:
p(f(rnd) >= f(d)): 0.001
p(f(rnd) <= f(d)): 0.999
Test Diagnostics:
Test Value (f(d)): 0.1545855
Replications: 1000
Distribution Summary:
Min: -0.1511055
1stQ: -0.03134596
Med: 0.0004905909
Mean: 0.001314569
3rdQ: 0.03400113
Max: 0.1582018
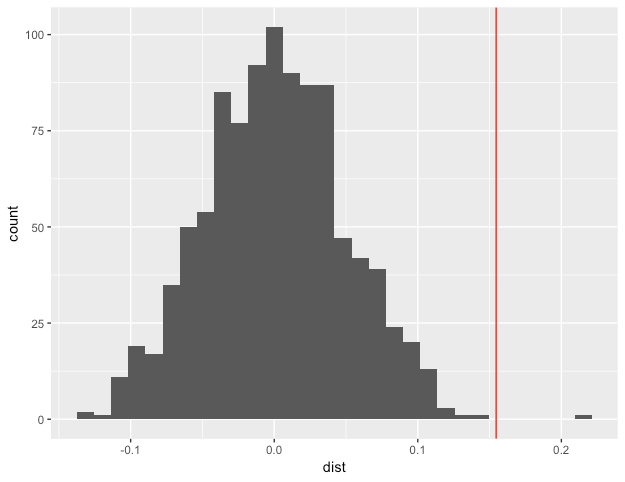
p=0.001とかなり小さい値であることから、これらのネットワークの相関は有意であると言えます。
分布で見てみるとこんな感じでした。
次に、1つのネットワークにおいても、サイズや密度を固定した場合の指標が取りうる可能性を検定することを検討します。
この時cugtest関数ではなくcug.test関数を用います。
FRIENDのネットワークにおいて、サイズと密度を固定した場合での、推移性の有意性を検定します。
引数にcmode = "edges"を指定することでサイズと密度を固定することができます。
第二引数には検定したい指標の関数を指定します。
> # 推移性の検定(サイズと密度を固定)
> gtrans(FRIEND)
[1] 0.4610526
> cug_gtrans <- cug.test(FRIEND, gtrans, cmode = "edges")
> print(cug_gtrans)
Univariate Conditional Uniform Graph Test
Conditioning Method: edges
Graph Type: digraph
Diagonal Used: FALSE
Replications: 1000
Observed Value: 0.4610526
Pr(X>=Obs): 0
Pr(X<=Obs): 1
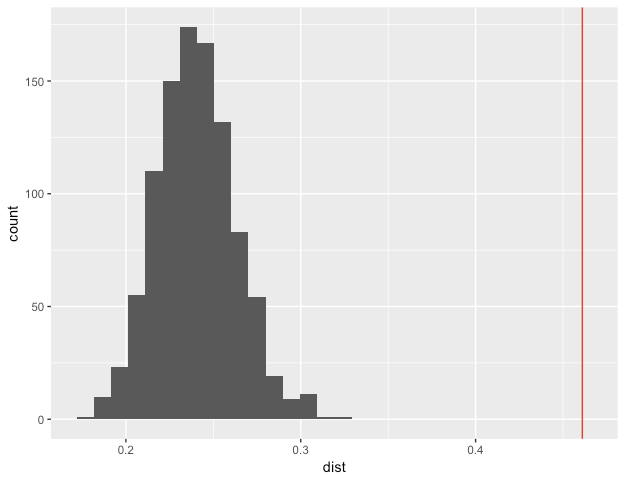
確率は0であり、FRIENDの推移性は同じサイズや密度と比べ、有意に高いと言えます。
分布を見てみると極めて高いことがわかります。
次にネットワークの密度が大きいか小さいかを検定することを考えます。
ネットワークのサイズは一定でエッジが存在する確率を0.5と固定し、密度の分布を求めることで検定を行います。
cug.test関数の引数をcmode="size"とすることでエッジの存在確率を固定することができます。
> # 密度の検定(辺が張る確率が0.5に固定)
> gden(FRIEND)
[1] 0.2428571
> cug.gden <- cug.test(FRIEND, gden, cmode="size")
> print(cug.gden)
Univariate Conditional Uniform Graph Test
Conditioning Method: size
Graph Type: digraph
Diagonal Used: FALSE
Replications: 1000
Observed Value: 0.2428571
Pr(X>=Obs): 1
Pr(X<=Obs): 0
エッジが存在する確率を0.5と固定すると、密度は有意に低いと言えます。
次にサイズのみを固定した場合の推移性に有意に低いか高いかを検証します。
引数をcmode="size"をするとサイズのみを固定できます。
> # 推移性の検定(サイズを固定)
> cug.gtrans2 <- cug.test(FRIEND, gtrans, cmode="size")
> print(cug.gtrans2)
Univariate Conditional Uniform Graph Test
Conditioning Method: size
Graph Type: digraph
Diagonal Used: FALSE
Replications: 1000
Observed Value: 0.4610526
Pr(X>=Obs): 0.896
Pr(X<=Obs): 0.104
サイズを固定した場合、有意な推移性ではなさそうです。
指数ランダムモデル
モデルについて
ノード間にあるエッジが確率的に存在すると考えるグラフをランダムグラフと呼びます。
ランダムグラフにおいて,ノード$i$と$j$の間にエッジが存在する確率は$p_{ij}$は次のようなロジスティックモデルで表現することができます。
p_{ij}=\frac{exp(\theta)}{1-exp(\theta)}
例えば、$\theta=0$の時、 $p_{ij}=0.5$となり、エッジをはるかは五分五分となります。
また、頂点$i$と$j$にエッジがある、かつ頂点$j$と$k$にエッジがある確率はそれぞれの積$p_{ij}p_{jk}$と表現することができます。
ここから、ランダムグラフにある全てのエッジの存在する確率は、各エッジの存在確率の累乗を求めることで得られます。
このようなランダムグラフ$Y$において、特定の構造をもつグラフが得られる確率は、パラメータ$\theta$を持つ次のような関数で表現できます。
P(Y=y) = \biggl( \frac{1}{c}\biggl) exp \bigl\{ \theta L(y)\bigr\}
ここで、$L(y)$は$y$に含まれる辺の数、$c$は確率が0から1を取るようにするための定数です。
このようなランダムグラフに関するモデルを指数ランダムモデル(ERGM)と呼びます。
そして、実際のネットワークでは、次数や相互性といった指標はランダムなグラフよりも有意に大きくなってしまう場合があります。
これらの指標を組み込んだモデルを$p_1$モデルと呼び、次のように表現します。
P(Y=y) = \biggl( \frac{1}{c}\biggl) exp \Bigl\{ \theta L(y) +
\sum_i^n \alpha_i y_{i+}+\sum_j^n \beta_j y_{+j}+\rho M(y)\Bigr\}
ここで、$\alpha_i$は頂点$i$がたの頂点に向けてエッジをだす度合い(外向性,拡張性)、$\beta_j$は頂点$j$がたの頂点からエッジを受け入れる度合い(人気度,魅力)を表現している。
そして、$y_{i+}$は頂点$i$の出次数、$y_{+j}$は頂点$j$の入次数、$M(y)$はネットワークに含まれる相互的な関係の数である。
また、$p_1$モデルでは、複数の二者間のエッジの有無は相互に独立であるという仮定がおかれている。
しかし、実際のネットワークでは、友人の友人は友人である確率が高いといったケースが観測されることが多く存在して、エッジの有無は相互に独立であるという仮定は成り立たないです。
この問題に対して有向マルコフグラフを導入することで解決ができています。
有向マルコフグラフは次の図のような含まれる2辺を取り出しても、必ず1つの頂点を共有しているようなグラフのことをさします。
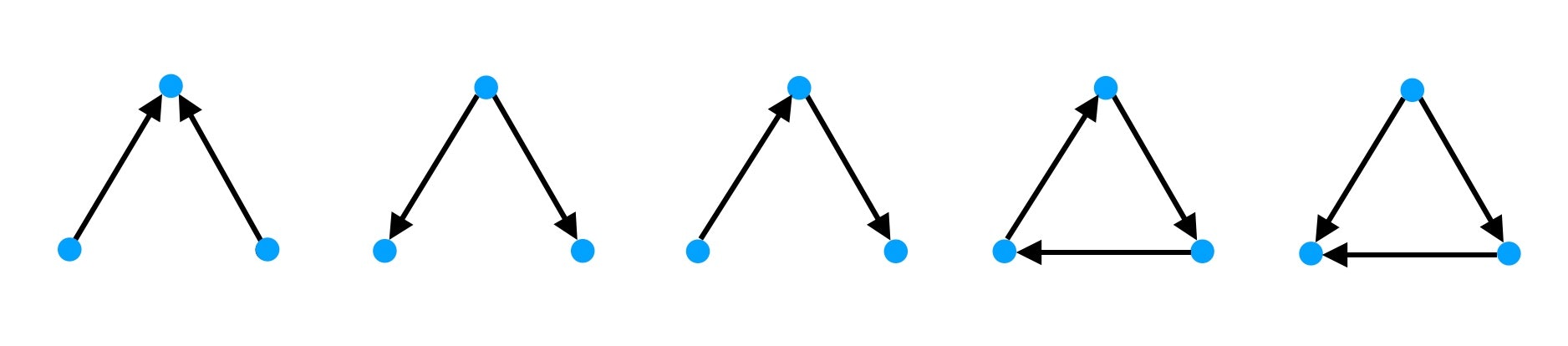
このようなグラフは1つの頂点を中心として$k$個の頂点が放射常に繋がっている構造であるといえ、k-スター構造と言います。
k=2の場合3頂点の有向マルコフグラフであり、7通り存在しています。kが増えていったとしても存在するパターンは限られます。
このパターンの存在をモデルに組み込んだマルコフグラフは次のように表現することができます。
P(Y=y) = \biggl( \frac{1}{c}\biggl) exp \Bigl\{ \theta L(y) +
\rho M(y) + \sum_{k=2}^{n-1} \sum_{i=0}^k \sum_{j=k-i}^k \sigma_{ijk} S_{ijk}(y)+\sum_{k=1}^7 \tau_k T_k(y) \Bigr\}
ここで、$S_{ijk}(y)$はネットワークに含まれるk-スターのタイプごとの数、$i$は中心の頂点に入る辺の数、$j$は中心の頂点からでる辺の数です。
$T_k(y)$は7つのタイプの三角形がそれぞれいくつ含まれる数を表しています。
そして、$p_1$モデルとマルコフモデルの両方を含む一般化した$p*$モデルが提案されており、次式で表現することができます。
P(Y=y) = \biggl( \frac{1}{c}\biggl) exp \Bigl\{ \sum_{k=1}^K \theta_k z_k (y)\Bigr\}
ここで、$z_k (y)$はエッジの数、相互的な関係の数、k-スターの数、三角形の数など、これまで出てきたネットワーク統計量であり、$\theta_k$はこれらの統計量の係数です。
また、類は共を呼ぶに例えられるような同じ属性のノード間にはエッジが生まれやすいという同類選好という考え方があります。
これもネットワーク統計量の一つとして扱うことができるようになります。
Rで指数ランダムモデル①
数式で考えるより、具体的なモデルがを作成する方がわかりやすいので、Rで分析を行なっていきます。
Rで指数ランダムモデルを実行するには、statnetパッケージに含まれるergmパッケージを利用します。
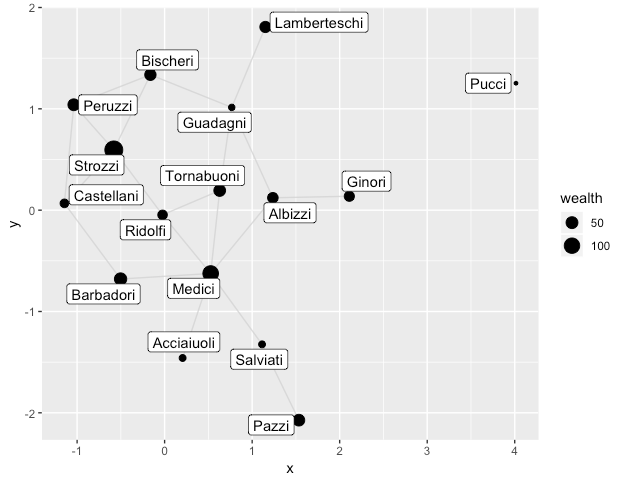
今回はパッケージ付属のサンプルデータである、ルネサンス期のフィレンツェの銘菓の婚姻関係のネットワークデータを用いて分析してみます。
初めにデータを確認してみましょう。
library(statnet)
data(florentine)
flomarriage_tbl <- as_tbl_graph(flomarriage)
# 富を重みにしたグラフ化
flomarriage %>%
as_tbl_graph() %>%
ggraph(layout = "kk") +
geom_edge_link(alpha=0.8, colour = "lightgray") +
scale_edge_width(range = c(0.1,1)) +
geom_node_point(aes(size = wealth)) +
geom_node_label(aes(label = name),repel = TRUE)
(Pucci...笑)
初めにエッジの数を説明変数としたモデルを作成します。
モデルの記述の仕方は、ergm関数を利用して回帰分析のモデルと同じように記述します。
なお、tidygraphとstatnetは互換性?がない(作者曰く、今後tidygraphでstatnetをラップする予定もない
)ため、ネットワークデータをそのまま使っていきます。
> # エッジのみを加味したモデル
> flomarriage.model.0 <- ergm(flomarriage ~ edges)
> summary(flomarriage.model.0)
==========================
Summary of model fit
==========================
Formula: flomarriage ~ edges
Iterations: 5 out of 20
Monte Carlo MLE Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -1.6094 0.2449 0 -6.571 <1e-04 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Null Deviance: 166.4 on 120 degrees of freedom
Residual Deviance: 108.1 on 119 degrees of freedom
AIC: 110.1 BIC: 112.9 (Smaller is better.)
得られた係数はエッジの数が1増加した時の対数オッズです。
続いては、エッジと三角形構造の存在を加味したモデルを検討して見ます。
> # エッジと三角形と加味したモデル
> flomarriage.model.1 <- ergm(flomarriage ~ edges + triangle)
> summary(flomarriage.model.1)
==========================
Summary of model fit
==========================
Formula: flomarriage ~ edges + triangle
Iterations: 2 out of 20
Monte Carlo MLE Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges -1.6639 0.3488 0 -4.771 <1e-04 ***
triangle 0.1408 0.5815 0 0.242 0.809
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Null Deviance: 166.4 on 120 degrees of freedom
Residual Deviance: 108.1 on 118 degrees of freedom
AIC: 112.1 BIC: 117.6 (Smaller is better.)
triangleの係数が正であることから三角形の数が1変化した時、ノード間にエッジがある確率は、増加すると言えそうです。
しかし、p値は大きいことから三角形の有無はエッジの存在確率に影響がないと考えられます。
このようなモデルの良さは一般の回帰分析のようにAIC,BIC基準を用いることで、評価することができます。
今回一番目のモデルが最も当てはまりが良いと判断することができます。
Rで指数ランダムモデル②
次にノードの属性や、二者間の関係を説明変数に加えたより説明力の高いモデルを作成します。
使うデータは検定でも用いたADVICEデータです。
# 属性の追加
ADVICE <- as.network(ADVICE)
age <- c(33,42,40,33,32,59,55,34,62,37,46,
34,48,43,40,27,30,33,32,38,36)
tenure <- c(9.333,19.583,12.75,7.5,3.333,
28,30,11.333,5.417,9.25,27,8.917,0.25,10.417,
8.417,4.667,12.417,9.083,4.833,11.667,12.5)
dpt <- c(4,4,2,4,2,1,0,1,2,3,3,1,2,2,2,4,1,3,2,2,1)
level <- c(3,2,3,3,3,3,1,3,3,3,3,3,3,2,3,3,3,2,3,3,2)
ADVICE %v% "age" <- age # 年齢
ADVICE %v% "tenure" <- tenure # 勤続年数
ADVICE %v% "dpt" <- dpt # 部署
ADVICE %v% "level" <- level # 階級
# 二者間の差分のデータを要因データとする
diff.age <- abs(sweep(matrix(age, nrow = 21, ncol = 21), 2, age))
diff.tenure <-
sweep(matrix(tenure, nrow = 21, ncol = 21, byrow = TRUE), 1, tenure)
diff.level <- sweep(matrix(level, nrow = 21, ncol = 21), 2, level)
モデルを生成し,パラメータ推定をおこないます。
そして、推定されたパラメータを確認します。
ノードのカテゴリカルな属性の影響はnodefacter()で指定できます。
同類選好の効果はnodematch()、二者関係の属性はedgecov()で指定できます。
また、ID13を基準とした牽引性(他のノードからの好意が集まるか)はreceiver、相互性はmutualで指定します。
> ADVICE_model <- ergm(ADVICE ~ edges + edgecov(diff.age) +
+ edgecov(diff.tenure) + edgecov(diff.level) + nodefactor("dpt") +
+ nodematch("dpt") + receiver(base = 13) + mutual)
> summary(advice.model.2)
==========================
Summary of model fit
==========================
Formula: advice ~ edges + edgecov(diff.age) + edgecov(diff.tenure) + edgecov(diff.level) +
nodefactor("dpt") + nodematch("dpt") + receiver(base = 13) +
mutual
Iterations: 3 out of 20
Monte Carlo MLE Results:
Estimate Std. Error MCMC % z value Pr(>|z|)
edges 2.88354 2.09891 0 1.374 0.169495
edgecov.diff.age -0.04408 0.01688 0 -2.611 0.009020 **
edgecov.diff.tenure 0.10015 0.02444 0 4.098 < 1e-04 ***
edgecov.diff.level 0.20941 0.33816 0 0.619 0.535757
nodefactor.dpt.1 -3.21499 0.94975 0 -3.385 0.000712 ***
nodefactor.dpt.2 -1.78547 0.96579 0 -1.849 0.064500 .
nodefactor.dpt.3 -1.32043 0.90893 0 -1.453 0.146297
nodefactor.dpt.4 -3.29927 0.98916 0 -3.335 0.000852 ***
nodematch.dpt 0.63513 0.28820 0 2.204 0.027536 *
receiver1 3.49553 1.00420 0 3.481 0.000500 ***
receiver2 4.40362 1.24726 0 3.531 0.000415 ***
receiver3 -0.92999 0.87712 0 -1.060 0.289022
receiver4 2.39262 0.98197 0 2.437 0.014829 *
receiver5 -0.08449 0.85182 0 -0.099 0.920989
receiver6 1.58060 1.17380 0 1.347 0.178120
receiver7 -1.75221 1.93043 0 -0.908 0.364047
receiver8 2.41293 0.99919 0 2.415 0.015740 *
receiver9 0.19508 0.89916 0 0.217 0.828237
receiver10 0.21908 0.97445 0 0.225 0.822116
receiver11 -0.55554 1.12678 0 -0.493 0.621989
receiver12 1.89197 0.99869 0 1.894 0.058166 .
receiver14 0.60756 0.86537 0 0.702 0.482630
receiver15 -0.92658 0.86946 0 -1.066 0.286558
receiver16 2.92033 0.96258 0 3.034 0.002414 **
receiver17 2.21387 1.01021 0 2.191 0.028416 *
receiver18 1.62446 1.02620 0 1.583 0.113425
receiver19 -0.57098 0.88811 0 -0.643 0.520279
receiver20 0.02755 0.83478 0 0.033 0.973672
receiver21 3.45582 1.06541 0 3.244 0.001180 **
mutual 1.26732 0.42480 0 2.983 0.002851 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Null Deviance: 582.2 on 420 degrees of freedom
Residual Deviance: 423.1 on 390 degrees of freedom
AIC: 483.1 BIC: 604.3 (Smaller is better.)
年齢、勤続年数が大きく影響するようです。
部署1と4は、同類選好の効果があると言えます。
また、ID13はID1,2,4,8,16,17,21と牽引関係にあると言えます。
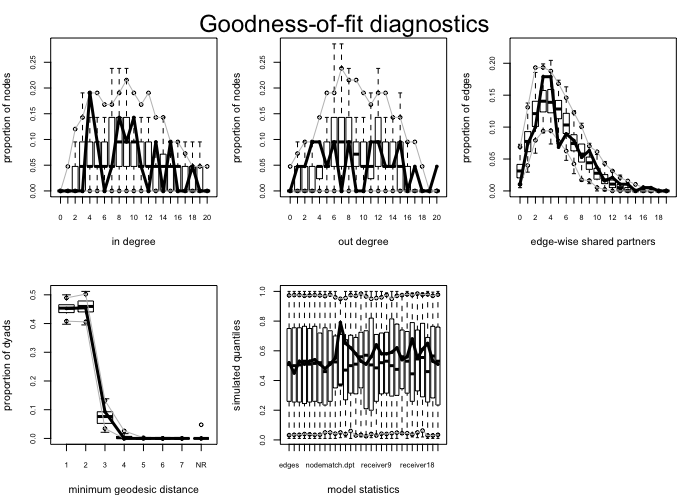
次に、モデルからネットワークをシミュレーションにより生成、元のネットワークの指標と比較しモデルの評価をおこないます。
ボックスプロットがシミュレーションにより得られたデータであり、実線が元のネットワークの指標です。入次数と出次数の分布が観測値を違いが少しあるようです。
Siena
ネットワーク構造は時間とともに変化していくものです。
このような継続的なネットワークのデータの統計的モデルと分析する方法としてSiena(Simulation Investigation for Empirical Network Analysis)が存在します。
Sienaモデルについて
社会ネットワークにおいて、アクター0(基準ノード)がある時点の他のアクターとの関係や行動に基づいて、次の時点の他者との関係や行動を決定する過程を確率的にモデル化する方法は確率的アクター指向モデルと呼ばれる。
モデルは評価関数で表現されることが多い。
現状のネットワークを$x^0$、決定の結果得られる次時点のネットワークは$x$、また決定の結果生じ得る全てのネットワーク集合をCとすると、次時点のネットワークの確率$P(x,x^0,C)$は次のように表現することができる。
P(x,x^0,C)=\frac{exp(u(x^0,x))}{\sum_{x' \in C} exp(u(x^0,x'))}
この時の、目的関数$u$をどのように定義するかが、分析の中心となる。
最も基本的なモデル(目的関数)では、次点におけるエッジの有無にのみ注目する評価関数の増分を用いて次のように定義される。
u(x^0,x)=f_i(x)-f_i(x^0)
ここで、$f_i(x)$は、$x$におけるノード$i$の評価関数である。
一般には効果の線型結合で表現され次のように定義される。
f_i(\beta,x)=\sum_k \beta_k s_{ki}(x)
$s_{ki}(x)$は様々な特立変数を表す関数であり、密度や相互性、推移性等の効果を意味している。
そして目的関数は、形成関数$c_i(x)$や保持関数$e_i(x)$を加えると一般的に次のようになります。
u(x^0,x)=f_i(x)-f_i(x^0) + \Delta^+(x^0,x)(c_i(x)-c_i(x^0))+\Delta^-(x^0,x)(e_i(x)-e_i(x^0))
また、$\Delta^+(x^0,x)$は、$x^0$より$x$の方がエッジが1つ多い時1を取り、それ以外は0を取る。
$\Delta^+(x^0,x)$は、$x^0$より$x$の方がエッジが1つ少ない時1を取り、それ以外は0を取る。
この作用により、エッジが増えた時に形成関数の増分、減った時に保持関数の増分がモデルに追加されることになります。
このように、目的関数でネットワークの変化を柔軟に表現することがSienaのと特徴です。
RでSiena
RでSienaはRSienaパッケージを用いることで実行することができます。
用いるデータはパッケージに付属しているサンプルデータで、スコットランドにおける50人の女子学生の関係データ(3回の観測)です。
また、それぞれの飲酒と喫煙のデータがあります。
library(RSiena)
data(s501)
# データの確認
plot_tbl_directed_data <- function(data, title){
data %>%
as_tbl_graph(directed = TRUE,mode = "out") %>%
ggraph(layout = "kk") +
geom_edge_link(alpha=0.8, colour = "#424242",arrow = arrow(length = unit(2, 'mm')), end_cap = circle(2, 'mm')) +
scale_edge_width(range = c(0.1,1)) +
geom_node_point() +
ggtitle(title) +
coord_fixed()
}
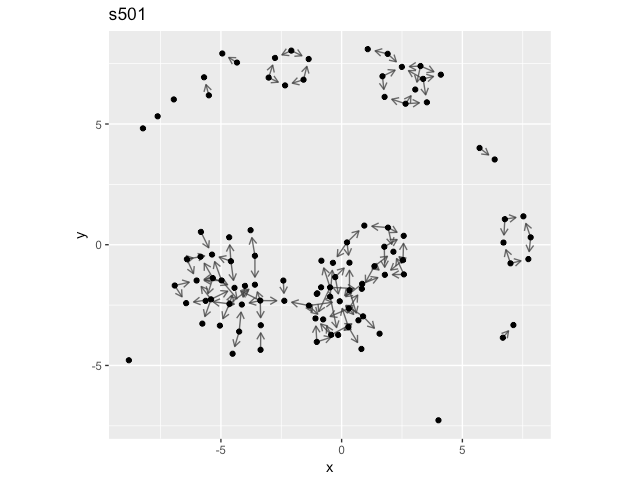
plot_tbl_directed_data(s501, title = "s501")
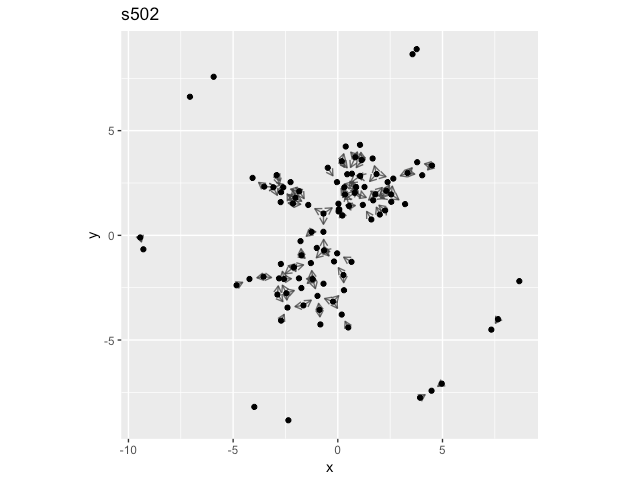
plot_tbl_directed_data(s502, title = "s502")
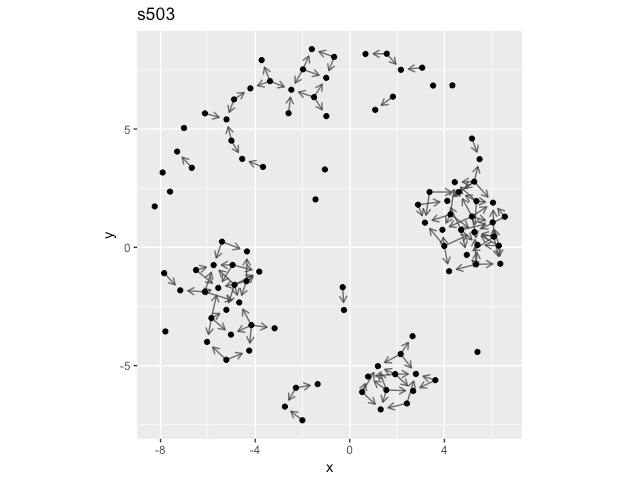
plot_tbl_directed_data(s503, title = "s503")
(ggraphでノードの位置を固定したかったですが、うまくいきませんでした)
次にモデル作成をするためにデータを整形していきます。
初めに、ネットワーク構造を説明変数するオブジェクトを作成します。
friendship <- array(c(s501,s502,s503), dim = c(50,50,3))
friendship <- sienaDependent(friendship)
次に、飲酒を時間変化する変数、喫煙を時間変化しない説明変数としてオブジェクトを作成します。
alcohol <- varCovar(s50a) #varCovar:時間変化する変数オブジェクトを生成
smoke <- coCovar(s50s[,1]) #coCovar:時間変化しない変数オブジェクトを生成
これらの変数オブジェクトをまとめてデータを説明変数オブジェクトを作成します。
> mydata <- sienaDataCreate(friendship, alcohol, smoke)
> mydata
Dependent variables: friendship
Number of observations: 3
Nodeset Actors
Number of nodes 50
Dependent variable friendship
Type oneMode
Observations 3
Nodeset Actors
Densities 0.046 0.047 0.05
Constant covariates: smoke
Changing covariates: alcohol
次にモデルに含める効果のオブジェクトを作成します。
myeff <- getEffects(mydata)
effectsDocumentation(myeff)
そして、モデルの推定を行います。
myproject <- sienaAlgorithmCreate(projname = "s50")
resalt <- siena07(myproject, data=mydata, effects=myeff)
推定中はこのようなウィンドウが立ち上がります。

推定結果を確認します。summaryで結果を見ることが来ますが、siena.tableで綺麗な表を出力することができます。
summary(resalt)
siena.table(resalt, type="html", sig = T)
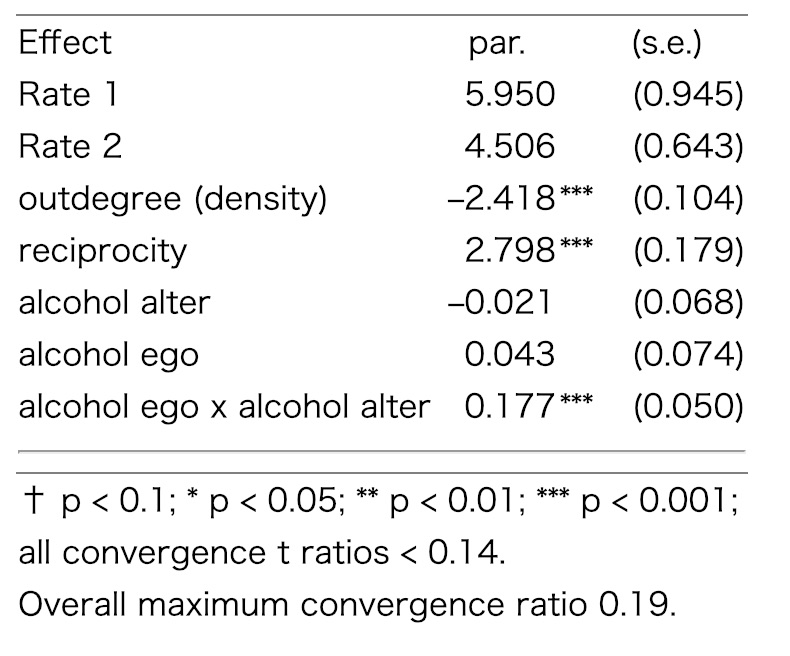
最後にモデルの当てはまりの確認します。
こちらも作成したモデルで、ネットワークデータをシミュレーションにより発生させ、比較します。
# モデルの当てはまりの診断
resalt <- siena07(myproject, data=mydata, effects=myeffect, returnDeps = TRUE)
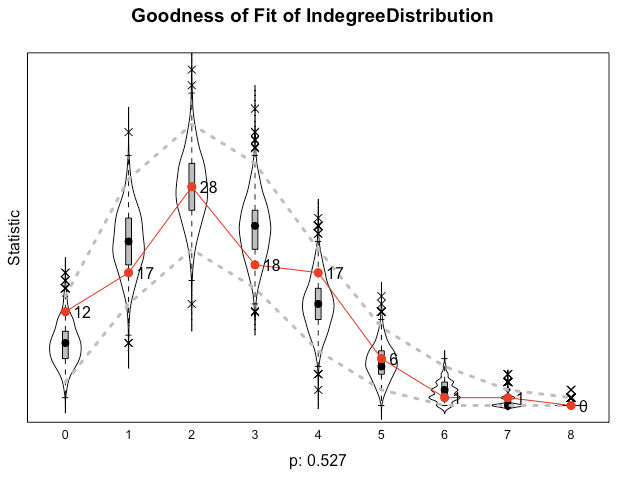
gofi <- sienaGOF(resalt, IndegreeDistribution, varName = "friendship", cumulative = FALSE, join=TRUE)
plot(gofi)
入次数の分布が得られましたが、観測値とシミュレーションによりえられたデータで大きな違いはなさそうです。
おわりに
統計的ネットワーク分析編は以上です。
ネットワークも統計的に扱えることが非常に刺激的でした。
次は、何かのデータを分析してみるか、複雑ネットワークについてまとめたいなと思います。
別のものを挟むかもしれませんが。