Stanでジョジョの奇妙な冒険 Part5のフォロー数モデリング

はじめに

松浦健太郎さん著の「RとStanで楽しむベイズ統計モデリング」通称アヒル本を読みました。
非常にわかりやすい本でした。
せっかくなので何かデータを利用してベイズ統計モデリングを行おうと思いました。
また、夏に行われたTokyoRにおいてMrUnadonさんのヴァイオレット・エヴァーガーデンのツイッターアカウントのフォロワー数の推移をStanによりモデリングしたお話が非常に印象に残っていました。
そこで、MrUnadonさんをモデリングを参考(ほぼそのまま)に私もジョジョの奇妙な冒険 黄金の風のアカウント@anime_jojoのフォロワー数の推移を統計モデリングしていきます。

データの取得

今回のコードはほとんどMrUnadonさんのコードを利用しております。
すみません&ありがとうございます。

フォロワー数のデータの取得を行いました。
Twitterのアニメ系アカウントのフォロワーを取得できるAPIからフォロワー数のデータを取得しています。
今回はアニメ放送開始日の10月5日から12月10日まで取得しました。

library(RCurl)
library(rlist)
library(rjson)
library(RcppRoll)
library(tidyverse)
library(anytime)
library(formattable)
library(lubridate)
library(scales)
library(shinystan)
library(ggmcmc)
library(rstan)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)

year <- 2018
#アニメシーズン:ベクトル（1=冬、2=春、3=夏、4=秋: 複数指定可能）
season <- 4
#現在から何時間前までのデータを取得するか
end_time <- 1
#50時間 ✕ 何回分のデータを取得するか
sampling <- 37

# 区切り位置の決定
subtract_UNIXtime<-c()
for(t in 1:sampling){
  subtract_UNIXtime[t]<-c((((60*30*100)*t)-(60*30*100))-3)}
end<-c(as.numeric(Sys.time())-c(end_time*60))
endP<-round(c(end-subtract_UNIXtime)-180000,0)

# フォロワーの履歴を取得
follower_history<-data.frame(matrix(NA,0,5))
for(t in 1: sampling){
  tmp_Res <- paste("http://api.moemoe.tokyo/anime/v1/twitter/follower/history?account=anime_jojo&end_date=",endP[t],sep="") %>%
    sprintf("account") %>% 
    list.load("") %>% 
    list.ungroup() 
  for(u in 1 : (length(tmp_Res) / 2 )){
    follower_history[(length(follower_history$X1)+1),]<-c(2018,1,"jojo",as.numeric(unlist(tmp_Res[[2*u]][1])),as.numeric(unlist(tmp_Res[[(2*u)-1]][1])))
  }
}

# 
base <- data.frame(Date = as.Date(seq(as.POSIXct("2018-10-04"), as.POSIXct("2018-12-15"), by = "days")))
jojo_df.org <- follower_history %>% 
  mutate(Year = as.integer(X1),
         Season = as.integer(X2),
         Title = as.factor(X3),
         UnixTime = as.integer(X4),
         Follower = as.integer(X5)) %>%
  mutate(Time = as.POSIXct(as.Date(anytime(as.numeric(UnixTime),tz = "Asia/Tokyo"))),
         Date = lubridate::date(Time)
  ) %>% 
  select(Year, Season, Title, Time, Date, Follower) %>%
  group_by(Date) %>%
  arrange(desc(Time), .by_group = TRUE) %>%
  distinct(Date, .keep_all = TRUE) %>%
  ungroup() %>%
  right_join(base) %>%
  full_join(data.frame(Date = lubridate::date(as.POSIXct(c("2018-10-04"))) + (seq(1:24) * 7 - 6),
                       OnAir = rep(1),
                       OnAirDate = lubridate::date(as.POSIXct(c("2018-10-04"))) + (seq(1:24) * 7 - 6))) %>%
  arrange(Date) %>%
  replace_na(list(OnAir = 0)) %>%
  fill(Year, Title, Season, .direction = "down") %>%
  filter(Date > as.POSIXct("2018-10-01") & Date < as.POSIXct("2018-12-10"))%>%
  mutate(OnAir = ifelse(OnAir == 1, "放送日", "非放送日")) %>%
  drop_na(Follower) %>% 
  as.data.frame()

saveRDS(jojo_df.org, file = "jojo_df_org.Rdata")

データの可視化

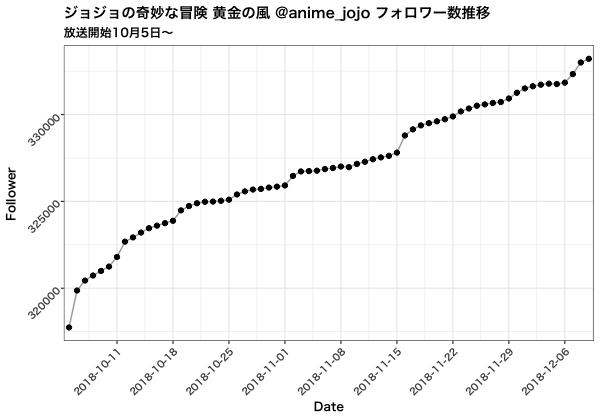
アニメ放送開始からのフォロワー数の変化を見てみます。

# フォロワー増加量を計算
jojo_df <- jojo_df.org %>% 
  mutate(lag_Follower = lag(Follower))%>%
  mutate(delta = Follower - lag_Follower) %>% 
  slice(-c(1)) 

# フォロワー数のトレンドをグラフ化
gp <- ggplot(jojo_df) + 
  theme_bw(base_size = 9, base_family = "HiraKakuProN-W6") +
  geom_line(aes(x = Time, y = Follower), colour = "darkgray") +
  geom_point(aes(x = Time, y = Follower)) +
  scale_x_datetime(expand = c(0.01, 0.01), breaks = scales::date_breaks("7 days")) +
  theme(axis.text = element_text(hjust = 1, angle = 45)) +
  scale_colour_manual(values = c("#6495ED", "#CD2626")) +
  labs(title = "ジョジョの奇妙な冒険 黄金の風 @anime_jojo フォロワー数推移",
       subtitle = "放送開始10月5日〜",
       x = "Date") 

print(gp)

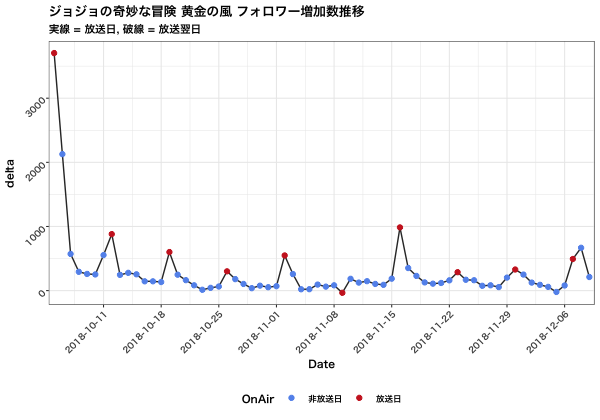
次に、フォロワーの増加量の推移を見てみます。

# フォロワー数の推移をグラフ化
gp2  <- ggplot(jojo_df) + 
  theme_bw(base_size = 8, base_family = "HiraKakuProN-W6")+
  geom_line(aes(x=as.POSIXct(Time),y=delta), colour = "gray20")+
  geom_point(aes(x=as.POSIXct(Time),y=delta, colour = OnAir))+
  scale_x_datetime(expand = c(0.01, 0.01), breaks = scales::date_breaks("7 days"))+
  theme(axis.text = element_text(hjust = 1, angle = 45)) +
  scale_colour_manual(values = c("#6495ED", "#CD2626")) +
  labs(title = "ジョジョの奇妙な冒険 黄金の風 フォロワー増加数推移",
       subtitle = "実線 = 放送日, 破線 = 放送翌日",
       x = "Date") + 
  theme(legend.position = "bottom", legend.direction = "horizontal") 

print(gp2)

データ理解

基本挙動

初回放送時に大きくフォロワーを獲得し、その後は大幅に減少、放送回を繰り返していくごとに相対的に減少傾向にあることがわかります。

放送前のツイート&放送による効果

放送がある日は、その直前に比べて大きくフォロワー数が増えることがわかります。
これは、その夜の放送の宣伝を行うツイートが活発に投稿され、その影響によりフォロワー数が増加していると考えられます。
そして、フォロワー数は次の放送回までで減少していってます。

ツイート効果について

第７話の放送日である11月16日にフォロワーが毎週放送による増加よりも多くフォロワーが増加していることがわかりました。
ジョジョ好きの友だちに相談してみたりしたところ、以下の11月16日のツイートが大きくリツイート/いいねがされており、その影響により普段よりフォロワーが多く増えたと考えられます。

【第7話「セックス・ピストルズ登場 その①」放送情報】

★TOKYO MX
11月16日（金）25:05 ～

★毎日放送
11月16日（金）26:55〜

★BS11
11月16日（金）25:30 ～

※放送時間は変更になる場合がございます#jojo_anime pic.twitter.com/KqbSoigxo4

— TVアニメ『ジョジョの奇妙な冒険』公式 (@anime_jojo) 2018年11月16日

暗殺チームの話題性の効果

第10話にフォロワーが毎週の増加よりも多く増えています。
これは第10話に置いてパッショーネの暗殺チームのメンバー全員が登場したからだと考えられます。
原作では、このような描写はなくアニメオリジナルの展開です。
そのため、少しTwitter上で話題になっていたようです。

(かっこええの〜)

フォロワー増加量が負となっている

11/9と12/5にフォロワーが減少=増加量が負となっています。
アカウントに対してマイナスイメージをもちフォローを解除した人が多くいたと言えそうですが、本来あるフォロワーの増加分以上のフォローの外す人が多いとか考えにくいです。
また、今年の7月にTwitter社は偽アカウント等を削除する動きをはじめています。
そのため、この２日にアカウントの削除が行われたと考えました。
この時、純粋なフォロワーの増加数はアカウント削除によるマイナスで相殺され、適切に取得できていないと考え、欠損値として扱います。

モデリング

放送回をへるごとにフォロワー数が相対的に減っていくのを、次のように指数関数により表現します。

\mu_{base} = \frac{I}{1-\gamma_{base}･T_{term}}

ここで、$\mu_{base}$は放送日のフォロワー数であり、$I$は切片、$\gamma_{base}$は減少度合いを表すパラメータ、$T_{term}$は放送話数を意味します。

毎日のフォロワーの増加$\mu_{each}$を次のように表現します。

\mu_{each} = \mu_{base}･\gamma^T_{each} 

ここで、$\gamma_{each}$は毎週のフォロワーの減少を表現するパラメータであり、$T$は放送日からの経過日をあわらしています。
また、11月16日のツイートによる第７話の週のフォロワーの増加量を次にように表現します。

\mu_{each} = (\mu_{base}+R_1)･\gamma^T_{each} 

$R_1$は、ツイートによる効果を表しています。

そして、アニメオリジナル展開による第10話の週のフォロワーの増加量を次にように表現します。

\mu_{each} = (\mu_{base}+R_2)･R_3･\gamma^{T-1}_{each} 

$R_2$が放送日当日の効果上昇を表現し、$R_3$が展開の効果を表しています。

これらの数式をstanで実装すると次にようなコードとなります。
こちらもほとんどMrUnadonさんのコードを利用させてもらっています。

model/jojo_follower_model.stan

data{
  int TimeLength;
  int TermLength;
  int TermPoint[TimeLength];
  real Y[TimeLength];
  int TermIndex[TimeLength];
  real TermBase[TermLength];
  int TermNo[TermLength];
  int base_NumNA;
  int each_NumNA;
}

parameters {
  real<lower=0> base_gamma;
  real<lower=1, upper=1500> R1;
  real<lower=1, upper=1000> R2;
  real<lower=1> R3;
  real<lower=0, upper=1> each_gamma;
  real base_pred_Y[base_NumNA];
  real each_pred_Y[each_NumNA];
  real<lower=0> base_sigma;
  real<lower=0> each_sigma;
}

transformed parameters {
  real<lower=0> base_mu[TermLength];
  real<lower=0> each_mu[TimeLength];
  
  for (i in 1:TermLength) {
    base_mu[i] = TermBase[1] / (1 + base_gamma * (TermNo[i] - 1)); 
  }

  for (j in 1:TimeLength) {
    if (TermIndex[j] == 7) {
      each_mu[j] = (base_mu[TermIndex[j]] + R1) * each_gamma ^ TermPoint[j];
    } else if (TermIndex[j] == 10) {
        if (TermPoint[j] == 1) {
          each_mu[j] = (base_mu[TermIndex[j]] + R2) * each_gamma ^ TermPoint[j];
        } else{
          each_mu[j] = (base_mu[TermIndex[j]] + R2) * R3 * each_gamma ^ (TermPoint[j]-1);
        }
    } else {
      each_mu[j] = base_mu[TermIndex[j]] * each_gamma ^ TermPoint[j];
    }
  }
}

model {
int na_ind_base;
  int na_ind_each;
  na_ind_base = 1;
  na_ind_each = 1;

  for (i in 1:TermLength) {
    if (TermBase[i] != -9999) {
      TermBase[i] ~ normal(base_mu[i], base_sigma);
    } else {
      base_pred_Y[na_ind_base] ~ normal(base_mu[i], base_sigma);
      na_ind_base = na_ind_base + 1;
    }
  }
  
  for (j in 1:TimeLength) {
    if (Y[j] != -9999) {
      Y[j] ~ normal(each_mu[j], each_sigma);
    } else {
      each_pred_Y[na_ind_each] ~ normal(each_mu[j], each_sigma);
      na_ind_each = na_ind_each + 1;
    }
  }
}

Stan用にデータを形成していきます。

stan_df <- jojo_df %>%
  mutate(delta = if_else(delta<0, NA_integer_, delta)) %>% 
  mutate(
    TimePoint = 1:nrow(delta_df),
    stan_delta = ifelse(is.na(delta), -9999, delta),
    Term = c(rep(c(1:9), each = 7),
             rep(10, nrow(delta_df) - length(c(rep(c(1:9), each = 7))))
    )
  ) %>%
  group_by(Term) %>%
  mutate(
    TermPoint = row_number(),
    TermBase = ifelse(TermPoint == 1, stan_delta, NA)
  ) %>%
  ungroup() %>%
  tidyr::fill(TermBase, .direction = "down")

# stan用にデータ整形
Term_dat <- stan_df %>%
  distinct(Term, .keep_all = TRUE) 
TimeLength <- max(stan_df$TimePoint)
TermLength <- nrow(Term_dat)
TermPoint <- stan_df$TermPoint
TermIndex <- stan_df$Term
TermNo <- Term_dat$Term
TermBase <- Term_dat$TermBase
Y <- stan_df$stan_delta
each_NumNA <- sum(is.na(stan_df$delta))
base_NumNA <- sum(Term_dat$TermBase == -9999)

# stan用にリストを作成
stan_data <- list(
  TimeLength = TimeLength,
  TermLength = TermLength,
  TermPoint = TermPoint,
  Y = Y,
  TermIndex = TermIndex,
  TermNo = TermNo,
  TermBase = TermBase,
  base_NumNA = base_NumNA,
  each_NumNA = each_NumNA
)

そして、MCMC...

# モデルの読み込み
Jojo_Model <- stan_model("v")

# サンプリングの実行
fit <- sampling(Jojo_Model,
                data = stan_data,
                seed = 42,
                iter = 2000,
                warmup = 1000
)

結果

サンプリングが収束しているか確認してみます

> all(summary(fit)$summary[,"Rhat"] <= 1.1,na.rm=T)
[1] TRUE

全てのパラメータにおいて収束しているのを確認できました。
得られたモデルの出力を確認してみます。

gp3 <- ggplot(resalt_df, aes(x = as.POSIXct(as.Date(Time)))) +
  theme_bw(base_size = 8, base_family = "HiraKakuProN-W6")+
  geom_vline(aes(xintercept = as.POSIXct(OnAirDate)), linetype = 1, colour = "gray")+ 
  geom_hline(yintercept = 0, size=0.3, linetype=2, colour="gray50")+
  geom_line(aes(y=delta), colour = "darkgray")+
  geom_point(aes(y=delta, colour = factor(OnAir)))+
  geom_ribbon(aes(ymax = upper, ymin = lower), alpha = 0.7) +
  geom_line(aes(y = EAP), alpha = 1, size = 0.2) +
  scale_x_datetime(expand = c(0.01, 0.01), breaks = scales::date_breaks("7 days"))+
  theme(axis.text = element_text(hjust = 1, angle = 45)) +
  scale_colour_manual(values = c("#6495ED", "#CD2626")) +
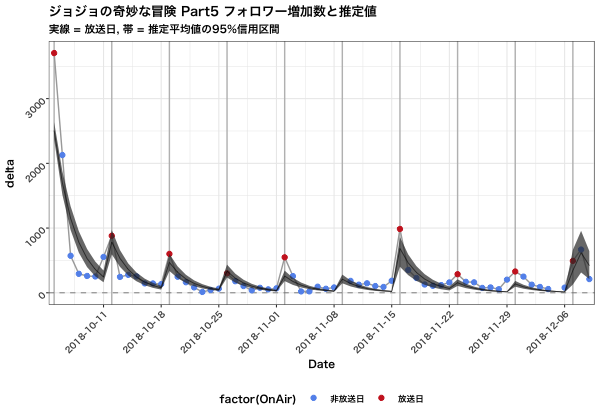
  labs(title = "ジョジョの奇妙な冒険 Part5 フォロワー増加数と推定値",
       subtitle = "実線 = 放送日, 帯 = 推定平均値の95%信用区間",
       x = "Date") + 
  theme(legend.position = "bottom", legend.direction = "horizontal") 

print(gp3)

放送回が増えるごとにフォロワー数の増加量は減少し、各放送日には増加しその後減少していくという挙動が捕らえられています。
そして、第７話と第１０話の放送におけるフォロワーの増加も表現できています。

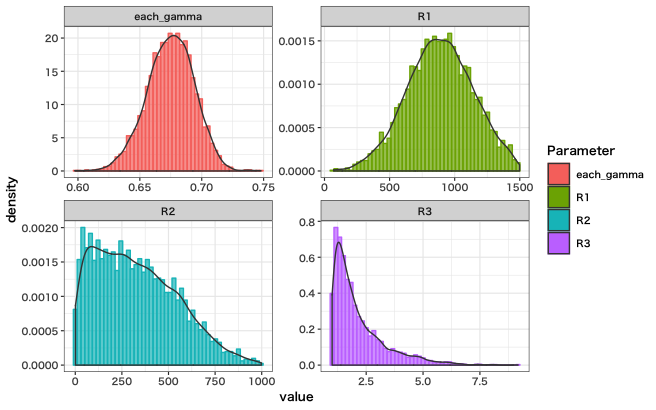
次にパラメータの分布を見ていきます

# パラメータの抽出
params <- samples %>%
  filter(str_detect(Parameter, "each_gamma") |
         str_detect(Parameter, "R1") |
         str_detect(Parameter, "R2") |
         str_detect(Parameter, "R3") 
  ) %>%
  select(Parameter, value)

# 分布図の作成
gp4 <- ggplot(params) +
  geom_histogram(mapping = aes(x = value, y = ..density.., fill = Parameter, colour = Parameter), bins = 50, alpha = 0.7) +
  geom_density(mapping = aes(x = value), alpha = 1, colour = "#424242") +
  facet_wrap(~Parameter, scales = "free") +
  theme_bw(base_size = 9, base_family = "HiraKakuProN-W6") 

print(gp4)

$R_2$は推定幅が大きいですね。
次にパラメータの平均値を抽出します。

> summary(fit)$summary[c("each_gamma","base_gamma","R1","R2","R3"),"mean"]
 each_gamma  base_gamma          R1          R2          R3 
  0.6748234   2.2802723 887.1911810 327.4734147   2.1550143 

10月16日のツイートの効果$R_1$は+887ツイート程度であったことがわかります。
アニメオリジナル展開の話題性の効果$R_2,R_3$は、それぞれ+327ツイート、2.15倍であったことがわかりました。

終わりに

今回の(MrUnadonさんの)モデリングで、関数をモデリングするということがわかりました。
今までは分布を当てはめることが多かったため、非常に参考になりました。
これでまた、より柔軟なモデリングがでいるようになりそうです。
しかし、まだ慣れませんのでもう少し経験を積みたいと思います。
次は状態空間モデルをStanで実装してみたいと思います。