RandomForestの感度分析パッケージ:ForestFloor

はじめに

最近、学習モデルの説明性について少し調べています。
その中で、手軽に使えそうなランダムフォレストの感度分析を行うパッケージの存在を知りましたので、試していきます。

基本的には, 次の三つページを参考にしていただきました。
・https://www.slideshare.net/kato_kohaku/sensitivity-analysis-usingforestfloor
・http://kato-kohaku-0.hatenablog.com/entry/2016/08/04/202826
・https://www.rdocumentation.org/packages/forestFloor/versions/1.11.1/topics/forestFloor

RandomForestの感度分析

ランダムフォレストモデルを構築した際に、変数重要度を出力して、どんな変数が判別や回帰に影響しているのかを見ていきます。
また、partial dependency plot（PDP）を出力して、説明変数の値と分類の関係を見ることはできます。
しかし、説明変数を動かした時、予測値や分類の確率がどの向きにどの程度変動するのかはわまりません。
その部分を解決するのが感度分析であり、説明変数の一つが変化した際に、予測値や分類結果がどの向きにどの程度変動するのかをくわしく見ていきます。

回帰の場合は、各変数が目的変数をどれだけ増減させるかを調べることができます。

分類の場合は、ある説明変数によりノードが分割されると所属確率がどの程度増減していくのかを分析していきます。

ForestFloorパッケージ

ForestFloorパッケージを利用してRandomForestの感度分析を行います。
基本的にはリファレンスのサンプルコードにしたがっています。

回帰

randomforestパッケージでモデルを構築します

library(forestFloor)
library(randomForest)

obs = 5000 
vars = 8
X = data.frame(replicate(vars,rnorm(obs))) 
Y = with(X, X1^2 + 1.2*sin(X2*pi) + 2 * X3 * X4 - 0.5 * rnorm(obs) + 0.05*X6^3) #潜在関数を定義

# モデル構築
rf_model = randomForest(
  X,
  Y, 
  keep.inbag = TRUE,  
  importance = TRUE,  
  sampsize = 1500 ,   
  ntree = if(interactive()) 500 else 50 
)

# 感度分析のオブジェクトを生成
FF = forestFloor(
  rf.fit = rfo,      
  X = X,             
  binary_reg = FALSE  
)

グラフを表示します。

> print(FF)
this is a forestFloor_regression object 

      this object can be plotted in 2D with plot(x), see help(plot.forestFloor) 

      this object can be plotted in 3D with show3d(x), see help(show3d) 

      

      x contains following internal elements: 
  FCmatrix imp_ind importance isTrain X Y
> plot(FF)
[1] "compute goodness-of-fit with leave-one-out k-nearest neighbor(guassian weighting), kknn package"

上記でplotした目的変数の変化を色で示し、それらと説明変数との対応を示しています。

> Col=fcol(FF,3,orderByImportance=FALSE)
> plot(FF,col=Col,plot_GOF=TRUE)
[1] "compute goodness-of-fit with leave-one-out k-nearest neighbor(guassian weighting), kknn package"

X3の変動と目的変数の変動を大きく対応しているようです。
また、X4のばらつきも対応していることがわかります。

続いて、３次元plotを行いました。

> show3d(ff,3:4,col=Col,plot_GOF=TRUE,orderByImportance=FALSE)

実際は、X11による表示なのでマウスでグリグリできます。

２クラス分類

次にirisデータからvirginicaのデータを除いて２クラス分類を行います。

set.seed(1234)
library(forestFloor)
library(randomForest)
data(iris)
X = iris[-1:-50,!names(iris) %in% "Species"] #drop third class virginica
Y = iris[-1:-50,"Species"]
Y = droplevels((Y)) 

rf_model = randomForest(
  X,Y,               
  keep.forest=TRUE,  
  keep.inbag=TRUE,   
  samp=20,           
  importance  = TRUE 
)

FF = forestFloor(rf_model,X,
                 calc_np=TRUE,    
                 binary_reg=TRUE) 
Col = col(FF,1) 
plot(FF,col=Col)   

Petal.LengthとPetal.Widthが判別に大きく影響していることがわかります。
次に３次元プロットです。

> show3d(FF,1:2,col=Col,plot.rgl.args = list(size=2,type="s",alpha=.5))

irisデータでの多クラス分類

set.seed(1234)
library(forestFloor)
library(randomForest)

data(iris)
X = iris[,!names(iris) %in% "Species"]
Y = iris[,"Species"]

rf_model = randomForest(
  X,Y,               
  keep.forest=TRUE,  
  keep.inbag=TRUE,   
  samp=20,           
  importance  = TRUE 
)

FF = forestFloor(rf_model,X)

plot(FF,plot_GOF=TRUE,cex=.7,
     colLists=list(c("#FF0000A5"),
                   c("#00FF0050"),
                   c("#0000FF35")))

Petal.widthとPetal.Lengthが３種類の分類に大きく寄与していることがわかります。

さらに、変数と所属確率への影響を見るために、simplex plotを行います。

こちらでも、Petal.widthとPetal.Lengthが所属確率の差を生み出していることを確認できます。

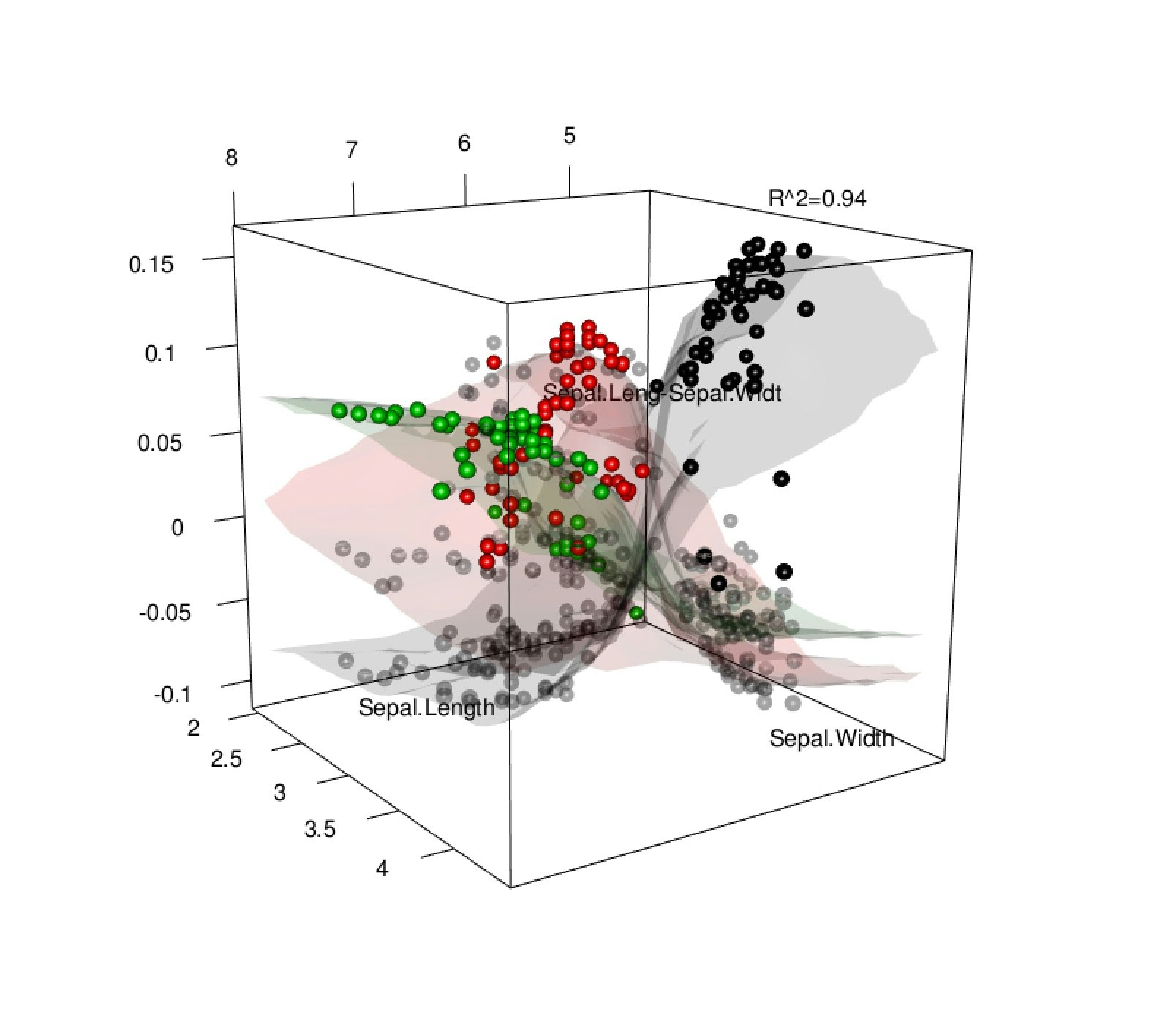
最後に、３次元plotをしてみます。
私のMPBではこれだけで結構重い...

> show3d(FF,1:2,1:2,plot_GOF=TRUE)