はじめに
最近selective labels(選択ラベル)が存在するタスクにおける学習を検討することがあり、「Learning under selective labels in the presence of expert consistency」という論文を読みましたので紹介します。
この論文では、選択ラベル問題があるデータを用いて汎用的な学習機を作成する場合に、バイアスのない学習を行うことを検討しています。
2種類の操作を適用することにより、ラベルが得られているデータのみの学習よりも予測が精度が向上したことも報告しています。
また、サンプルデータを使って、予測精度の改善が見込まれるのかを検証しました。
検証に用いたRコードはGithubにあげています。
機械学習初心者の自分ですので、論文はこういうことを意味していたんだ!解釈違うだろ!などを指摘してもらえるとありがたいです。
論文内容
題材
児童相談所にかかってくる電話相談から、家庭内問題が起こっているか/起こりうるかを機械学習で予測したいです。
現状はケースワーカー(専門家)が、電話内容から追加調査を行なった方が良いかを判断しています。
追加調査の結果、問題があったかを知ることができます。このように、タスクの性質によりラベルが得られるかどうかにバイアスが生まれてしまいます。

今回用いているデータは、2010~2014年の47,305人の子供に関する83,311件の電話相談のデータです。
説明変数は800種以上(詳細は不明)であり、電話から730日間ケースワーカーがフォローした結果がラベルとして得られています。
これらのデータには対して次の2つの操作を適用することで、高い予測精度が見込まれることを主張しています。
-
Data Augmentation
ラベルが得られていないデータ(black box部分)も利用できそうな部分を学習データに取り入れ水増しする -
Semi synthetic labels
より確信度の高いラベルを貼り直す
それでは、具体的な説明をしていきます。
はじめにselective labels問題についてです。
Selective Labels
Selective Labelsとは、ラベルが得られるまで2段階の(人間の)意思決定や割り振りを経ることで、ラベルが得られないデータセットとラベルが得られたデータセットが発生してしまうような状態をさします。
ラベルが得られているデータのみので学習してしまうと、新しいデータに対する予測精度が著しく低下する可能性があります。
ラベルが得られているデータでは、1段階目の意思決定により本来のデータの分布の一部分のみを選択したバイアスのある状態になっているためです。
少し表現を変えると学習データと検証データで分布の剥離がある状態であるためです。
Selective Labelsという言葉は、「The Selective Labels Problem: Evaluating Algorithmic Predictions in the Presence of Unobservables」( H.Lakkaraju et al., KDD2017)で定義しています。
この論文では、裁判官が少年犯罪者を釈放するかどうかを判断するかどうかを検討しています。
釈放後、再犯罪を行わないよう人を人間の意思決定と同じように機械学習により精度よく予測を行いたい。
しかし、釈放を認めた人しか再犯罪を犯したかのデータが得られないselective labels状態であり、このデータのみで学習してしまうとバイアスのある予測しか得られません。
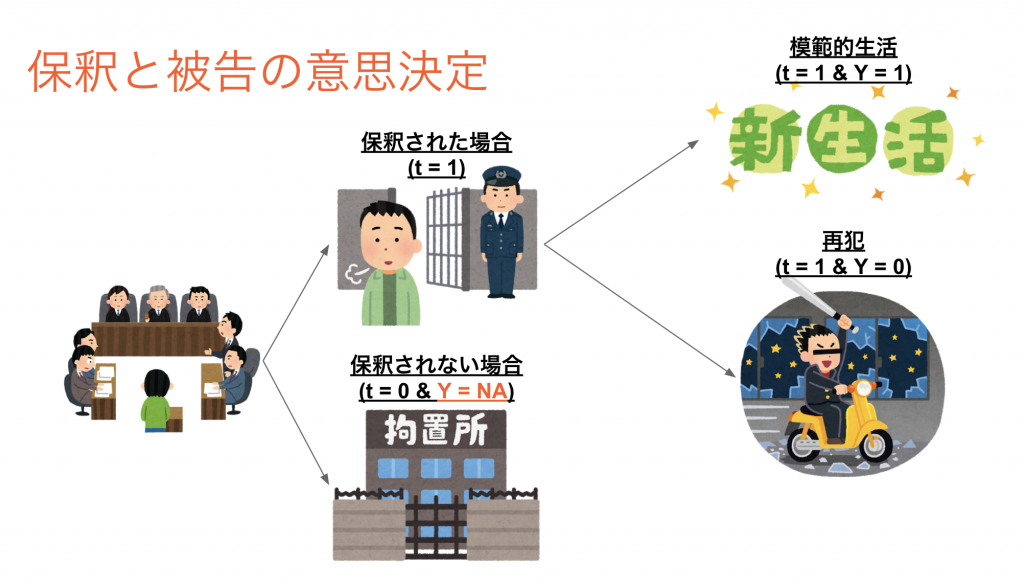
以下の仮定の元で、Contraction tecniqueと呼ばれるバイアスのないモデルの予測精度の評価が行える手法を提案しています。
- 複数の裁判官がいること
- 裁判官の保釈決定にムラがあること
- 裁判官への案件の割り当てはランダムであること
詳しくは、サイバーの安井さんの記事が非常にわかりやすいです。
今回の児童相談所の課題では、人間の決定にムラはあまりなく、同一の予測を行う問題であると考えられています。
Data augumentation
ラベルが得られていないサンプルの中には、ケースワーカー(=専門家)が確信を持って追加調査しないと判断した部分があるはずです。
それに対応するデータは「追加調査なし」とラベルをふり学習データとして使って良いはずです(実際のラベルの振り方は次の部分で紹介します)。
以下の図で言うと一番右の図における左下のサンプルです。

サンプル$i$における得られている情報を$x_i$、ラベルを$y_i$とし、追加調査を行うかを$d_i={1,0}$で表現します。
このとき、ラベルが得られているデータセット$S_o$と水増しデータを含めたデータセット$S_A$は次のように表現できます。

ここで、$P(d_i=1|x_i)$は追加調査に割り当てられる確率、$\epsilon$は、確信を持って追加調査を行なったサンプルを定義するための閾値です。
追加調査に割り当てられる確率$P(d_i=1|x_i)$は、追加調査割り当てをランダムフォレストで学習させて得られた割り当て確率を用いています。
論文では、学習させたランダムフォレストモデルの予測結果$P(d_i=1|x_i)$を次のようになったそうです。

Semi senthetic labels
対象としている児童相談所の問題では、取りこぼしが発生した時のコストやインパクトが大きいため。少しでも疑わしいものは追加調査を行います。
しかし、取りこぼしがないようにすると外れが多くなってしまします。
これはRecallが高いがPrecisionが低い判断している状態であるといえます。
この判断は、病気の診断等の様々な判断において実際に採用されている判断の状態です。
この判断を機械学習に対しても実行してもらうために、論文では次のように表現されるようにラベル$y_i^s$を再付与することを提案しています。
論文中では明記されていませんが、右辺を1.0に近い値にした際の新しいラベルにおけて、(0.5付近を割り当ての閾値にした場合に)Recallが非常に高くなる状態を実現できます。
このようなことを表現しようとしていると考えられますが、真意はうまく汲み取れませんでした。

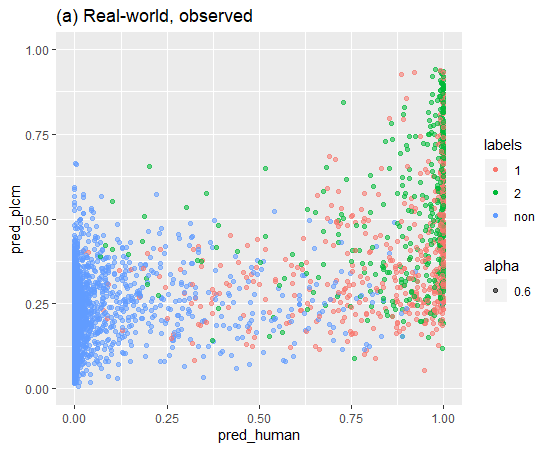
そして、ラベルの再付与の効果を次のような図を作成することで、経験的に確認ができるとしています。
横軸は人間の1段階目の意思決定を表現しており、実際は割り当てを表現するランダムフォレストモデルによる予測確率の出力値です。
縦軸は、機械学習による意志決定を表現しており、学習したモデルによる予測確率の出力値です。この学習モデルには何を用いたのかの詳細は記載されていませんでした。
それぞれのモデルの学習は、キャプションで示しているデータで行なっています。
グラフ作成に用いるデータを生成するための推定には、テストデータを用いています.
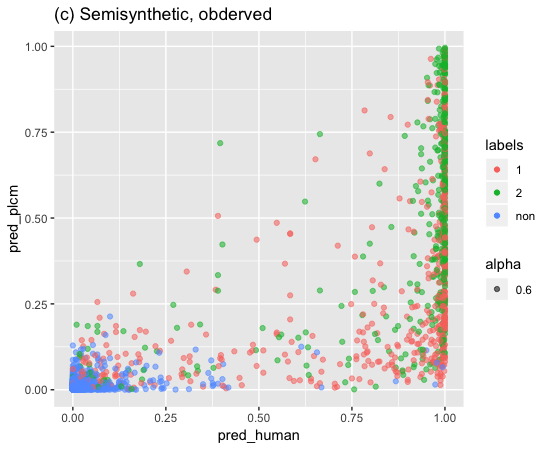
論文では、図(c)のラベルの再付与のみを行なった場合のデータセットで学習した場合、ラベルが得られていないデータ(グラフにおける青色のサンプル)における人間による意思決定は確率0付近に集中していますが、機械学習による意思決定の確率はバラついています。
そのため、ラベルが得られていないデータにおける人間の意思決定と機械学習のよる意思決定と剥離があることを主張していました。
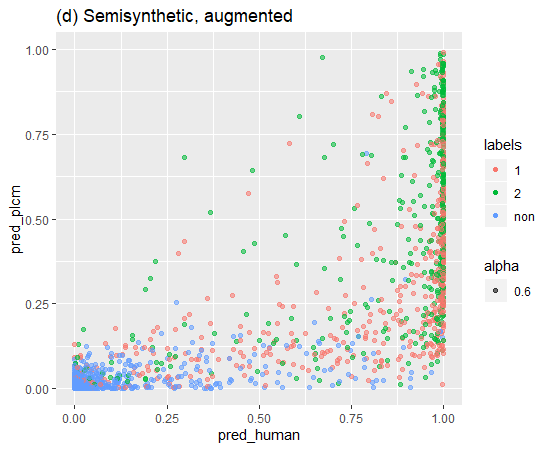
一方で、図(d)のラベルの再付与と水増しを行なったデータセットで学習した結果では、ラベルが得られていないデータの割り当て確率は両軸共に0付近に集中しています。
そのため、人間の意思決定と機械学習のよる意思決定が一致していると主張していました。

結果
予測精度がどの程度改善されるのかをAUCを基準に検証した結果です。
なお、ここで用いられた機械学習モデルの詳細は、記載されていませんでした。
結果として、水増しやラベル再付与単体(b)(c)では予測精度の向上はありませんでした。
水増しとラベル再付与の両方(b)だと、予測精度の大幅な向上が達成できることが確認できました。
なお、IPWによるバイアス補正は予測精度への影響はほぼなかったそうです。

サンプルデータで検証
サンプルデータで論文のアルゴリズムを適用して、本当に予測精度が向上するのかを確認する
データはkaggleに置いてある銀行のマーケティングデータを用いました。
カラムは17個で全体45,211レコードであり、うちキャンペーン効果があった顧客レコードは5,289件でした。
selective labelsの検討
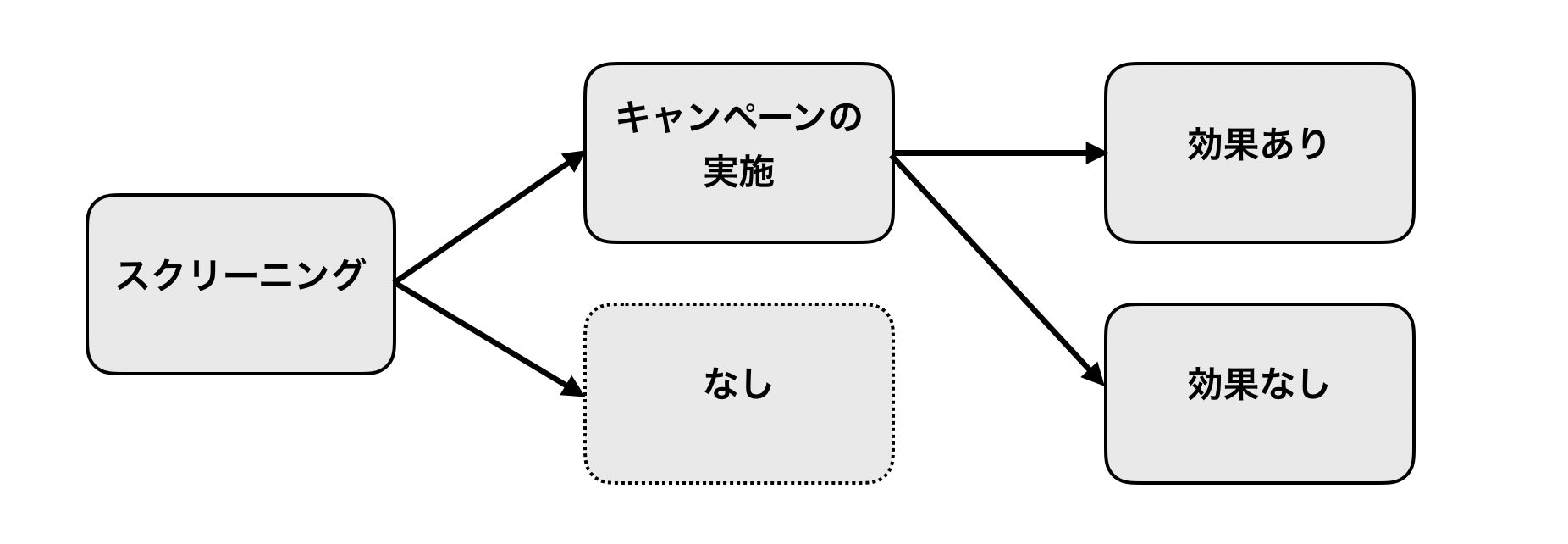
selective labels状態を実現するために、以下の図のような流れでラベル内容が決定するように設定しました。
全ての顧客に対して一度スクリーニングを行い、キャンペーン効果が高い顧客のみを抽出します。
この顧客のみにキャンペーンを実施して、「効果あり(契約獲得)」か「効果なし(契約未獲得)」のラベルが得られます。
スクリーニングで弾かれた顧客にはキャンペーンを実施しなかったため、ラベルが得られません。
内容
これを実現するために、はじめにデータを三等分しました。
データを4:4:2に分割しスクリーニングモデル用データ、学習用データ、検証用データとしました。
スクリーニングモデル用データを用いて、XGBoostモデル学習しました。
なお、この検証で用いる機械学習モデルは、caretパッケージで実装したものであり、パラメータはデフォルトを用いました。
また、予測確率からキャンペーン効果があるかを判断するための閾値は、Recallが0.8程度になるように調整しています。
作成したXGBoostを学習用データに適用して、キャンペーンを実施するかどうかの判別を行いました。
キャンペーンを実施と判別したデータだけを用いて、ラベルを予測するモデルを学習させました。これはバイアスのある学習であると言えます。
また、データを学習用データの全てを用いてモデルを学習させました。これはバイアスのない学習ができていると言えます。
ここで、この状態でどれぐらいバイアスがあるのかを10CVで確認しました。
| バイアスなし学習 | バイアスあり学習 | |
|---|---|---|
| 10CV AUC平均 | 0.9320 | 0.8246 |
やはりバイアスが存在してしまっていて、予測精度の低下が認められました。
次に、キャンペーンを実施の割り当て予測を行うモデルを作成して、データ水増しとラベルの再付与を行います。
キャンペーンを実施の割り当て予測を行うモデルにはランダムフォレストを用いました。
水増しに用いるデータを選択するためのパラメータ$\epsilon$は0.05と指定しました。
ランダムフォレストモデルによる割り当て予測の分布を確認すると次にようになりました。

そして、この確率分布を用いてSemi senthetic labelsの付与を行いました。
ラベルの付与を決める割り当て確率の閾値は0.9,0.8,0.7としました。
結果
論文にあった、割り当て確率と予測確率を縦と横軸にとったグラフを作成してみました。
赤が未成立、緑が成立、青がラベルなしを意味しています。
論文で示している通り、元の状態(a)に対して提案手法を適用すると(d)はラベルが得られていないデータは両軸において確率0の場所に集まっていることが確認ができます。
論文に則ると、提案手法による影響を経験的に確認できたようです。
次に、予測精度が改善するかを確認しました。
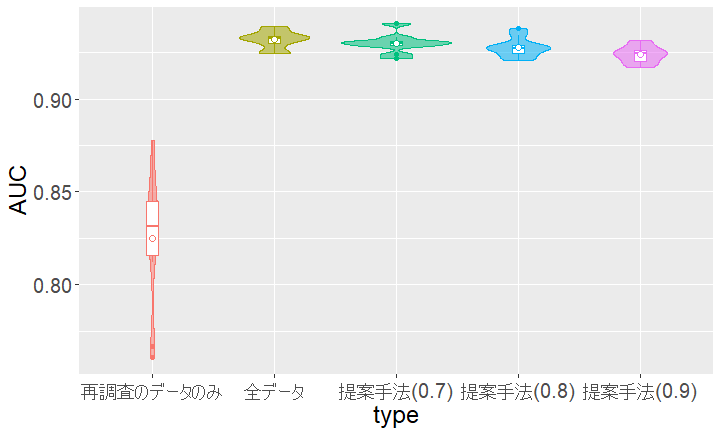
上記の操作を10CVで繰り返して得られた各モデルのAUCの分布は、次のバイオリンプロットのようになりました。
| バイアスなし学習 | バイアスあり学習 | 提案手法(閾値:0.7) | 提案手法(閾値:0.8) | 提案手法(閾値:0.9) | |
|---|---|---|---|---|---|
| 10CV AUC平均 | 0.9320 | 0.8246 | 0.9299 | 0.9278 | 0.9240 |
バイアスのない全データを学習した場合とほぼ同じ予測精度が得られていることが確認できます。
また、同様の検証をkaggleにおいてある心血管疾患の判別サンプルデータにおいても同様の
操作を行い、予測精度の改善が得られるかの確認を行いました。

こちらでも、バイアスのない全データを学習した場合とほぼ同じ予測精度が得られていることが確認できました。
所感
結局、なぜうまくいくのかは感覚的にはわかりますが、それをうまく表現できません。
また、論文内で必要な情報が少ない気もしています。
ラベルの再付与は割り当て確率による重み付けがバイナリになっているだけなのかなとも考えました。
そして、共変量シフトの問題として扱う方が良いのではないかと考えてしました。
よろしければ、機械学習初心者の足りない頭ではない頭脳で検証していただければ幸いです