はじめに
解釈性と自由度の高さから構造方程式モデリングを使いたいと考えています。
そのため、構造方程式モデリングの基礎を簡単に勉強してみました。
Rで行う場合ではlavaanパッケージを用いてモデリングが可能ですが、構造方程式モデリングの理解を深めるために、Rstanを用いたベイズ推定を行いたいと思いました。
基本的には、こちらとこちらの内容を自分用にまとめただけの内容です。
※足りない部分があるので、あとで加筆していきます。
構造方程式モデリング概要
直接観測できない潜在変数を導入し、潜在変数と観測変数との間の因果関係等を同定するための統計的モデリング手法です。
主に社会現象や自然現象を理解するために用いられることが多いです。
また、SEMは回帰分析、因子分析、分散分析、共分散分析の分析を内包しているため、これらを表現することも可能です。
モデリングとしては、以下の二つの方程式を組み合わせたものになります。
- 観測方程式:因子分析
- 構造方程式:(パス)回帰分析
測定方程式
x_i = \alpha_i f_1 +e_i (i=1,2,3) \\
E[e_i e_j] = 0 (i \neq j), E[f_i e_j] = 0 \\
E[f_i]=0, V[f_i]=1, E[e_i]=0, V[e_i]=\sigma^2_{e_i}
共分散を母数の関数で表現することを「構造化」と呼びます。
共分散を方程式モデルの母数で表現したものを「共分散構造」と呼び、次のように表現することができます。
\Sigma =
\begin{bmatrix}
\sigma_1^2 & &\\
\sigma_{21} & \sigma_2^2 &\\
\sigma_{31} & \sigma_{32} & \sigma_3^2\\
\end{bmatrix} =
\begin{bmatrix}
\alpha^2_{11} + \sigma_{e1}^2 & &\\
\alpha_{21} \sigma_{11} & \alpha^2_{21} + \sigma_{e2}^2 &\\
\alpha_{31} \sigma_{11} & \alpha_{31} \sigma_{21} &\alpha^2_{31} + \sigma_{e3}^2\\
\end{bmatrix}
測定方程式では$f$が平均,分散1に仮定しているので、計算するとパラメータだけになります。
測定方程式を行列表記する。
x = Af+e\\
E[f]=0\\
E[e]=0\\
E[fe]=0
共分散構造は以下のようになります。
\Sigma = A \Sigma_{rs} A' + \Sigma_e
ここで、$\Sigma_{rs}$は潜在変数の相関がある場合にパラメータが含まれます。
$\Sigma_{e}$は誤差関に相関がある場合にパラメータが含まれます。
構造方程式(パス回帰分析)
次にように矢印が刺さる変数を内生変数、矢印が刺さらない外生変数と呼びます。

v=Av+e
\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
\end{bmatrix} =
\begin{bmatrix}
0 & 0 & 0\\
\alpha_{21} & 0 & 0\\
0 & \alpha_{32} & 0\\
\end{bmatrix}
\begin{bmatrix}
v_1 \\
v_2 \\
v_3 \\
\end{bmatrix} +
\begin{bmatrix}
e_1 \\
e_2 \\
e_3 \\
\end{bmatrix}
残差は他の変数から説明されなかった残りであるため、今回は$v_1$も残差となります。
そして、自己回帰は考えていないため、Aの体格成分は常に0です。
観測方程式と構造方程式を統一した形にする
観測方程式と構造方程式を1つの式として表現すると次のようなります。
\begin{bmatrix}
f \\
v \\
\end{bmatrix} =
\begin{bmatrix}
A_a & A_d\\
A_b & A_c\\
\end{bmatrix}
\begin{bmatrix}
f \\
v \\
\end{bmatrix} +
\begin{bmatrix}
d \\
e \\
\end{bmatrix}
ここで、$d$は$f$に関する残差変数、$e$は$v$に関する残差変数です。
この表現から、観測方程式と構造方程式は次のように分解して表現することができます。
\begin{bmatrix}
f \\
v \\
\end{bmatrix} =
\begin{bmatrix}
0 & 0\\
A_b & 0\\
\end{bmatrix}
\begin{bmatrix}
f \\
v \\
\end{bmatrix} +
\begin{bmatrix}
d \\
e \\
\end{bmatrix}
\begin{bmatrix}
f \\
v \\
\end{bmatrix} =
\begin{bmatrix}
0 & 0\\
0 & A_c\\
\end{bmatrix}
\begin{bmatrix}
0 \\
v \\
\end{bmatrix} +
\begin{bmatrix}
0 \\
e \\
\end{bmatrix}
共分散構造は次のように表現できます。
G=[I, 0]\\
T=(I-A)^{-1}\\
\Sigma = GT\Sigma_aT'G'\\
\Sigma_u =
\begin{bmatrix}
\Sigma_d & \Sigma_{de}\\
\Sigma_{ed} & \Sigma_e\\
\end{bmatrix}
```
これらのパラメータは最尤推定を用いて求めていく形になります。
# lavaanパッケージで構造方程式モデリング
Rでの構造方程式モデリングはlavaanパッケージで行うことができます。
今回利用したデータは、lavaanパッケージに含まれているPoliticalDemocracyデータを用います。
このデータにはBollenの1989年の書籍で構造方程式モデリングを行うために利用された、発展途上国における政治の民主主義と工業化に関するさまざま数値が含まれています。
```R
library(tidyverse)
library(lavaan)
library(semPlot)
```
SEMの定義を行います。
お手本にならって潜在変数を3つ仮定したモデルを定義しました。
lavaanパッケージでは、潜在変数(因子)と観測変数の関係は"~="で表現し、潜在変数の右辺から左辺への因果関係は"~"、潜在変数の相関関係と観測変数の残差共分散は"~~"で表現します。
```R
# モデル定義
create_Model <- function() {
# 変数名 ∼ 依存変数
# + 依存変数の合成
return ("
# 潜在変数の定義
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# 回帰
dem60 ~ ind60
dem65 ~ ind60 + dem60
# 残差共分散
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
")
}
```
モデルの推定を行います。
```R
model <- create_Model()
res_sem <- cfa(model, data= PoliticalDemocracy)
```
推定された結果を確認しまます。
```R
> summary(res_sem, standardized = TRUE)
lavaan 0.6-3 ended normally after 68 iterations
Optimization method NLMINB
Number of free parameters 31
Number of observations 75
Estimator ML
Model Fit Test Statistic 38.125
Degrees of freedom 35
P-value (Chi-square) 0.329
Parameter Estimates:
Information Expected
Information saturated (h1) model Structured
Standard Errors Standard
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
ind60 =~
x1 1.000 0.670 0.920
x2 2.180 0.139 15.742 0.000 1.460 0.973
x3 1.819 0.152 11.967 0.000 1.218 0.872
dem60 =~
y1 1.000 2.223 0.850
y2 1.257 0.182 6.889 0.000 2.794 0.717
y3 1.058 0.151 6.987 0.000 2.351 0.722
y4 1.265 0.145 8.722 0.000 2.812 0.846
dem65 =~
y5 1.000 2.103 0.808
y6 1.186 0.169 7.024 0.000 2.493 0.746
y7 1.280 0.160 8.002 0.000 2.691 0.824
y8 1.266 0.158 8.007 0.000 2.662 0.828
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
dem60 ~
ind60 1.483 0.399 3.715 0.000 0.447 0.447
dem65 ~
ind60 0.572 0.221 2.586 0.010 0.182 0.182
dem60 0.837 0.098 8.514 0.000 0.885 0.885
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.y1 ~~
.y5 0.624 0.358 1.741 0.082 0.624 0.296
.y2 ~~
.y4 1.313 0.702 1.871 0.061 1.313 0.273
.y6 2.153 0.734 2.934 0.003 2.153 0.356
.y3 ~~
.y7 0.795 0.608 1.308 0.191 0.795 0.191
.y4 ~~
.y8 0.348 0.442 0.787 0.431 0.348 0.109
.y6 ~~
.y8 1.356 0.568 2.386 0.017 1.356 0.338
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.x1 0.082 0.019 4.184 0.000 0.082 0.154
.x2 0.120 0.070 1.718 0.086 0.120 0.053
.x3 0.467 0.090 5.177 0.000 0.467 0.239
.y1 1.891 0.444 4.256 0.000 1.891 0.277
.y2 7.373 1.374 5.366 0.000 7.373 0.486
.y3 5.067 0.952 5.324 0.000 5.067 0.478
.y4 3.148 0.739 4.261 0.000 3.148 0.285
.y5 2.351 0.480 4.895 0.000 2.351 0.347
.y6 4.954 0.914 5.419 0.000 4.954 0.443
.y7 3.431 0.713 4.814 0.000 3.431 0.322
.y8 3.254 0.695 4.685 0.000 3.254 0.315
ind60 0.448 0.087 5.173 0.000 1.000 1.000
.dem60 3.956 0.921 4.295 0.000 0.800 0.800
.dem65 0.172 0.215 0.803 0.422 0.039 0.039
```
推定されたSEMの適合度を確認します。
SEMの適合度の指標は複数あります。
- $\chi^2$検定:(あまり当てにならないらしい)
- GFI:パラメータによって表現された共分散と、データによる共分散の差。1が最もよく、0.9以上必要されている.
- RMR:残差平方平均平方根、0が最もよい。
- AGFI:自由度修正済みのGFI。
- CFI:比較適合度指標。0から1までの値をとり、1がもっともよい。
- AIC:赤池情報量基準、複数のモデルの相対的な評価が行える。
lavaanパッケージでは、fitMeasures関数を用いることで、以上の指標を含めた様々な指標を同時に出力してくれます。
今回のモデルでは、$\chi^2$検定のp値は>0.05、CFIとGFIは0.9以上ありますが、AGFIは0.9以下です。
適当な適合度は満たせていると考えられますが、厳密な適合とは言えないのかもしれません。
```R
> fitMeasures(res_sem)
npar fmin chisq df
31.000 0.254 38.125 35.000
pvalue baseline.chisq baseline.df baseline.pvalue
0.329 730.654 55.000 0.000
cfi tli nnfi rfi
0.995 0.993 0.993 0.918
nfi pnfi ifi rni
0.948 0.603 0.996 0.995
logl unrestricted.logl aic bic
-1547.791 -1528.728 3157.582 3229.424
ntotal bic2 rmsea rmsea.ci.lower
75.000 3131.720 0.035 0.000
rmsea.ci.upper rmsea.pvalue rmr rmr_nomean
0.092 0.611 0.276 0.276
srmr srmr_bentler srmr_bentler_nomean crmr
0.044 0.044 0.044 0.049
crmr_nomean srmr_mplus srmr_mplus_nomean cn_05
0.049 0.045 0.045 98.970
cn_01 gfi agfi pgfi
113.803 0.923 0.854 0.489
mfi ecvi
0.979 1.335
```
推定された結果をパス図で表示したいと思います。
```R
semPaths(res_sem, "model", "est", intercepts = FALSE)
```

# Rstanによる構造方程式モデリング
本題です。
上記で行なったモデリングをRstanで行いたいと思います。
はじめに、観測変数は多変量正規分布に従います。
```math
X \sim multi\_normal(M, \Sigma)
```
共分散構造はlavaanの時と同様です。
```math
T = (I-A)^{-1}\\
M = G T A\\
\Sigma = G T \Psi T^{'}G^{'}
```
ここで、$G$は因子と項目を識別するための選択行列、$I$は単位行列、$A$はパスおよび因子負荷量を表す影響力行列、$\Psi$は分散と共分散を含むパラメータを行列にしたものです。A(alphaの大文字)は切片パラメータベクトルです。
stanコードは次にようになります。(ただの写経です)
rep_matrixで特定の値のマトリックスを定義できることを初めて知りました。
```R:sem_stan.stan
data{
int N; //サンプルサイズ
int P; //観測変数の数
int L; //潜在変数の数
int M; //影響力パラメータの数
int R; //共分散パラメータの数
int S; //分散パラメータの数
int A; //平均パラメータの数
int L_input[L+P,L+P]; // パス行列
int P_input[L+P,L+P]; // 分散共分散を表す行列
int A_input[L+P]; // 観測変数を意味するベクトル
vector[P] X[N]; //観測データ
}
parameters{
vector[A] alpha; // 影響力の行列
vector[M] lambda; // 因子負荷量
vector[R] rho; //潜在変数相関
vector<lower=0>[S] psy; //
}
transformed parameters{
vector[P] Mu;
cov_matrix[P] Sigma;
vector[L+P] Alpha;
matrix[L+P,L+P] Lambda;
matrix[L+P,L+P] Sigma_a;
Lambda = rep_matrix(0,L+P,L+P);
Sigma_a = rep_matrix(0,L+P,L+P);
//パラメータの入力
{
// インデックスを定義
int k1; int k2; int k3; int k4;
// インデックスを初期化
k1 = 0; k2 = 0; k3 = 0; k4 = 0;
Lambda = rep_matrix(0, L+P,L+P);
Sigma_a = rep_matrix(0, L+P,L+P);
for(i in 1:(L+P)){
if(A_input[i]==999){
k4 = k4 + 1;
Alpha[i] = alpha[k4];
}else{
Alpha[i] = A_input[i]; // 0を代入
}
for(j in 1:(L+P)){
if(L_input[i,j] == 999){
k1 = k1 + 1;
Lambda[i,j] = lambda[k1]; //推定された因子負荷量を代入
}else{
Lambda[i,j] = L_input[i,j]; // 0を代入
}
if(P_input[i,j] == 999){
if(i==j){
k2 = k2 + 1;
Sigma_a[i,j] = psy[k2];
}else if(i < j){
k3 = k3 + 1;
Sigma_a[i,j] = rho[k3];
}
}else{
Sigma_a[i,j] = P_input[i,j]; // 0を代入
}
}
}
}
// 共分散行列を計算する
{
matrix[P,L+P] G; //因子と項目の識別行列
matrix[L+P,L+P] T;
G = append_col(rep_matrix(0,P,L), diag_matrix(rep_vector(1,P)));
T = inverse(diag_matrix(rep_vector(1,L+P))-Lambda);
Sigma = G*T*Sigma_a*T'*G';
Mu = G*T*alpha;
}
}
model{
//観測変数についての多変量正規分布
X ~ multi_normal(Mu, Sigma);
alpha ~ normal(0, 10^2);
lambda ~ normal(0, 10^2);
psy ~ cauchy(0, 5);
rho ~ normal(0, 10^2);
}
```
そして、Rコードです。
```R
library(tidyverse)
library(rstan)
library(psych)
library(MASS)
library(lavaan)
# 並列処理のおまじない
rstan_options(auto_write=TRUE)
options(mc.cores=parallel::detectCores())
# 諸々のデータ整形
dat <- PoliticalDemocracy %>%
select(contains("x"),contains("y"))
N <- nrow(dat)
P <- ncol(dat)
L <- 3
L_input <- read_csv("L_input.csv", col_names = F)
P_input <- read_csv("P_input.csv", col_names = F)
A_input <- read_csv("A_input.csv", col_names = F)
M <- which(L_input==999) %>% length()
S <- which(diag(as.matrix(P_input))==999) %>% length()
R <- (length(which(P_input==999))-S)*0.5
A <- nrow(A_input)
lambda_init <- list(lambda=c(1,1,1,1,1,1,1,1,1,1,1))
sem_init <- list(lambda_init,lambda_init,lambda_init,lambda_init)
sem_data <- list(N=nrow(dat),P=P,L=L,M=M,S=S,R=R,A=A,
L_input=L_input,P_input=P_input,A_input=A_input[,1],X=dat)
# モデル読み込みとMCMC
sem_model <- stan_model("sem_stan_3f.stan")
fit.sem <- sampling(sem_model,
data = sem_data,
iter = 6000,
warmup = 2000,
chains = 4,
thin = 2,
init = sem_init)
推定された結果のサマリーを見て、収束しているかの確認します。
Rhatを確認すると全て1.05以下であるため、収束していると判断できます。
> print(fit.sem,pars=c("lambda","rho","psy"))
Inference for Stan model: sem_stan_3f.
4 chains, each with iter=6000; warmup=2000; thin=2;
post-warmup draws per chain=2000, total post-warmup draws=8000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
lambda[1] 1.43 0.02 0.38 0.70 1.18 1.42 1.68 2.21 626 1.01
lambda[2] 0.47 0.01 0.24 0.01 0.31 0.46 0.63 0.95 744 1.00
lambda[3] 0.87 0.01 0.12 0.65 0.78 0.86 0.94 1.14 334 1.02
lambda[4] 2.19 0.01 0.15 1.92 2.09 2.19 2.29 2.50 514 1.00
lambda[5] 1.83 0.01 0.16 1.53 1.72 1.82 1.93 2.15 680 1.00
lambda[6] 1.40 0.01 0.19 1.05 1.27 1.39 1.52 1.79 466 1.01
lambda[7] 1.08 0.01 0.16 0.77 0.97 1.07 1.18 1.42 530 1.01
lambda[8] 1.34 0.01 0.16 1.05 1.24 1.33 1.44 1.68 429 1.01
lambda[9] 1.27 0.01 0.18 0.96 1.14 1.26 1.37 1.68 430 1.01
lambda[10] 1.30 0.01 0.17 1.01 1.18 1.28 1.40 1.65 472 1.01
lambda[11] 1.33 0.01 0.17 1.04 1.21 1.31 1.43 1.70 433 1.01
psy[1] 0.48 0.00 0.10 0.32 0.41 0.47 0.54 0.70 731 1.00
psy[2] 3.98 0.04 0.98 2.36 3.29 3.87 4.56 6.21 478 1.01
psy[3] 0.30 0.01 0.21 0.02 0.14 0.26 0.42 0.80 877 1.01
psy[4] 0.09 0.00 0.02 0.05 0.07 0.09 0.10 0.14 666 1.00
psy[5] 0.14 0.00 0.08 0.02 0.08 0.13 0.19 0.30 600 1.00
psy[6] 0.51 0.00 0.10 0.34 0.44 0.51 0.58 0.75 778 1.00
psy[7] 2.16 0.02 0.49 1.37 1.82 2.11 2.43 3.29 676 1.01
psy[8] 6.69 0.05 1.26 4.58 5.79 6.56 7.45 9.50 733 1.01
psy[9] 5.56 0.03 1.01 3.87 4.85 5.45 6.17 7.85 899 1.00
psy[10] 2.99 0.02 0.67 1.85 2.52 2.93 3.40 4.42 1011 1.00
psy[11] 2.64 0.02 0.54 1.76 2.26 2.58 2.95 3.86 765 1.01
psy[12] 4.51 0.03 0.85 3.07 3.90 4.43 5.02 6.44 922 1.01
psy[13] 3.72 0.02 0.73 2.48 3.20 3.64 4.16 5.34 901 1.00
psy[14] 3.02 0.02 0.64 1.94 2.56 2.96 3.40 4.46 709 1.02
Samples were drawn using NUTS(diag_e) at Tue Jul 2 21:57:22 2019.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
また、自己相関の確認等は、最近だとshinystan::launch_shinystanを用いることが多いです。
以下のキャプチャはlambda[1]の結果です。
他のパラメータも含めて自己相関性があり、適切なサンプリングではなかったようです。
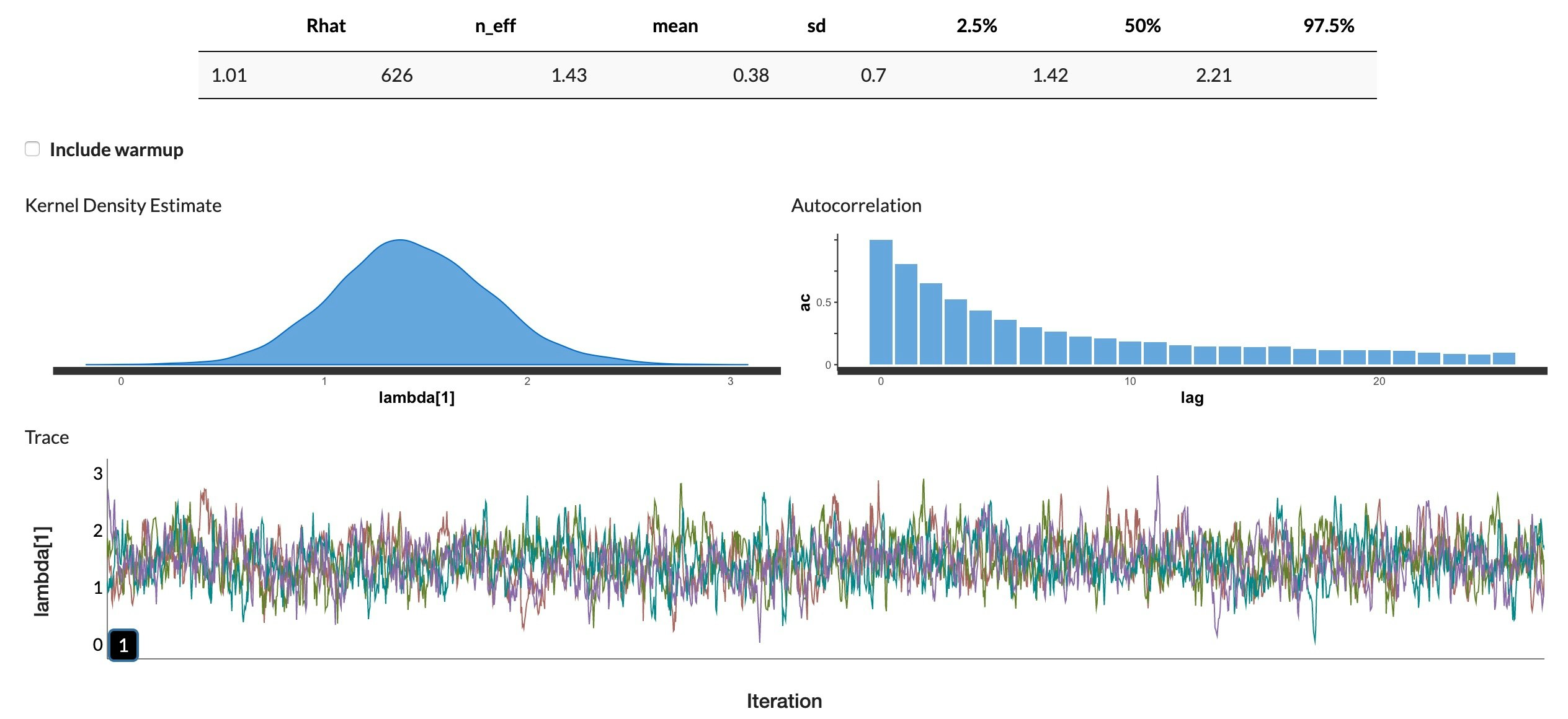
結果として、適切なサンプリングではなかったものの、lavaanと近しいパラメータの推定値が得られていると考えられます。
以上です。
参考
- http://www.ec.kansai-u.ac.jp/user/arakit/documents/lavaanTutorial20170124.pdf
- http://nekomosyakushimo.hatenablog.com/entry/2018/10/31/131244
- http://truestar.jp/main/metrics/basicstatistics/SEM%20Basic.pdf
- https://csrda.iss.u-tokyo.ac.jp/seminar2002_1.pdf
- http://www.mizumot.com/method/2012-05_Konno.pdf
