はじめに
統計的因果分析を勉強しようと本を開いてみましたが、グラフィカルモデリングの知識が必要なことがわかってきたので、宮川雅巳 著「グラフィカルモデリング」を読んでいっています。
理解を整理するために、少しまとめました。ただの個人的な備忘録です
また、グラフはDiagrammeRパッケージを利用して生成しました。
グラフィカルモデリングとできること
グラフィカルモデリングとは、確率変数の依存関係をグラフ表現するモデリングです。
確率変数を頂点、それらの間の依存関係を辺としたグラフを用いて表します。
そして、グラフ理論考え方と確率統計理論を融合させたモデリング方法です。
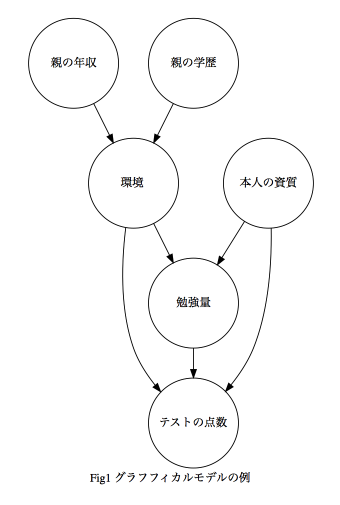
例として次のようなものがあげられます。これは学生のテストの点数と周辺の影響を表しています。(別にグラフどおりの因果関係があるわけではありません)
本人の資質や勉強量は確率変数を表す頂点です。
また、環境は親の年収と親の学歴に依存しているということを(矢印の)辺で表しています。
変数間の関係をグラフと統計量で表すができたり、グラフ構造から因果・相関関係の解釈に繋がったりします。
また、多変量のデータから変数間の関係を探索的に検討することもできます。
DiagrammeRによるグラフ作成
今回の記事で生成するグラフは、DiagrammeRパッケージを利用して作成していきます。
基本的な書き方はこのようなものです。
library(DiagrammeR)
# 最もシンプルなもの
grViz("
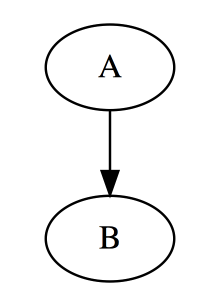
digraph test {
A -> B
}
")
各ノードや辺、そのほかの設定を行う場合は次のようになります。
graph[...]でラベルやフォントの設定を行います。
node[...]で頂点の形や色、名前の設定を行います。
edge[...]で辺の設定を行います。
grViz("
digraph dot {
graph [compound = true, nodesep = .5, ranksep = .5,
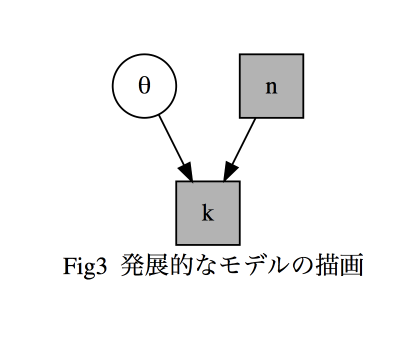
color = black, label='Fig3 発展的なモデルの描画']
node [shape = circle,style = filled,fillcolor = white,color = black,label = 'θ'] theta
node [shape = square,style = filled,fillcolor = grey,color = black,label = 'k'] k
node [shape = square,style = filled,fillcolor = grey,color = black,label = 'n'] n
edge [color = black]
theta -> k
n -> k
}",engine = "dot")
偏相関係数と独立グラフ
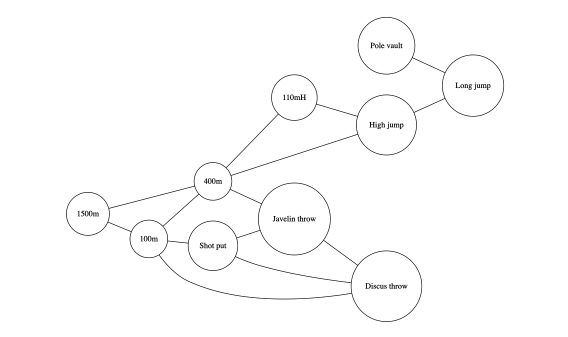
ここでは、陸上の10種競技の結果を多変量データとして考えていきます。
それぞれの競技の結果を変数とし、各変数ごとの相関係数を求め、変数の関係を調べていきます。
100mの結果と400mの結果は相関が高くなると考えられます。
しかし、同様のトラック競技である1500mの結果が、100mと400mの結果の両方に相関している可能性も考えられ、100mと400mの結果は相関は純粋な関係を表ていない可能性があります。
このような注目したい変数の関係において、他の変数の影響を除いてみたいと考えた場合、偏相関係数を用いて評価します。
相関行列を$R=(r_{ij})$と表した場合、この逆行列を$R^{-1}=(r_{ij})$と表す。
この時の変数$i$と変数$j$間の偏相関係数$r_{ij・rest}$の定義は次のような形になります。
r_{ij・rest} = \frac{- r^{ij}}{\sqrt{r^{ii}}\sqrt{r^{jj}}}
偏相関係数でそれぞれの変数間の相関をみていくと、0.0となる変数の対が出てきます。
変数を頂点とし、非0の相関係数をもつ変数間には辺を渡し、グラフを作成すると次にようなものになります。
このように作成されたグラフを独立グラフと呼びます。
ここで、独立グラフは相関が0であることを独立を意味していることからきています。
また、偏相関変数が0であることは条件付き独立であると呼ばれ、条件付き独立であることから作成したグラフを条件付き独立グラフと呼びます。
条件付き独立
2つの確率変数X,Yがあり、Xの分布がYによらない場合、今回では相関がない場合に、2変数は独立であると言います。
そして、3つ目の変数Z加えた場合を考えます。
Zをある値に固定する=条件付けた場合、XとYが独立である場合に2変数は条件付き独立であると呼びます。
条件付き確率の考え方は、因果推定の分野で重要な考え方です。
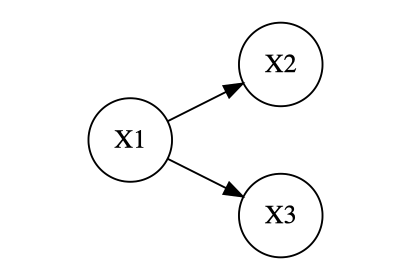
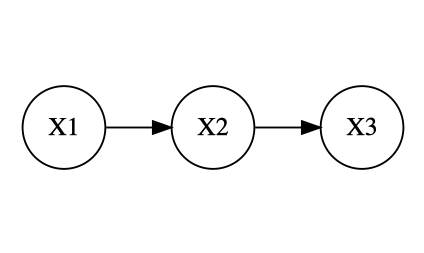
基本的な因果モデルとして、共通原因系モデルと連鎖因果モデルが挙げられ、次のような図で表すことができます。
両者の矢印を除けば同じモデルとなります。
 |
 |
|---|
事象の条件付き独立
事象をA,Bで表す。事象Bが生起したという条件のもと、Aが生起する条件付き確率は、P(B)>0において次のように定義される
P(A|B)=\frac{P(A\cap B)}{P(B)}
AとBが独立と言うことを次にように表す。
P(A\cap B)=P(A)P(B)
また、三つの事象Cを条件つけした場合の、AとBが独立であることは次のように表す。
P(A\cap B|C)=P(A|C)P(B|C)
確率変数の条件付き独立
三つの確率変数$x,y,z$の同時確率分布関数を$f(x,y,z)$と表す。
この場合のzを条件付けた場合の確率密度関数=条件付き密度関数は次にように表す。
f(x,y|z)=\frac{f(x,y,z)}{f(z)}\\
f(x,z)=\frac{f(x,z)}{f(z)}\\
f(y,z)=\frac{f(y,z)}{f(z)}
また、次の関係が成り立つ場合にXとYは独立であるといえる。
f(x,y)=f(x)f(y)
Zを与えたもとでXとYは、条件付き独立であるという。
f(x,y \mid z)=f(x \mid z)f(y \mid z)
因果分解基準
条件付き独立を判断には、次の関係を満たす関数gとhが存在することにより比較的簡単に判断することができます。
この基準を因果分解基準と呼びます。
f(x,y,z)=g(x,z)h(y,z)
無向独立グラフ
この辺に方向性がない場合、無向独立グラフと呼びます。
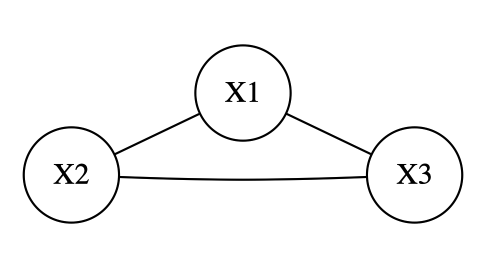
次のようなグラフをさします。

4つの確率変数において、次の2つの条件付き条件関係が成立しているとする。
X_1 \parallel X_4 \mid (X_2,X_3)\\
X_2 \parallel X_4 \mid (X_1,X_3)
条件付き独立が成り立つ変数間にはグラフ上の辺が存在せず、次のような無向独立グラフとなります。
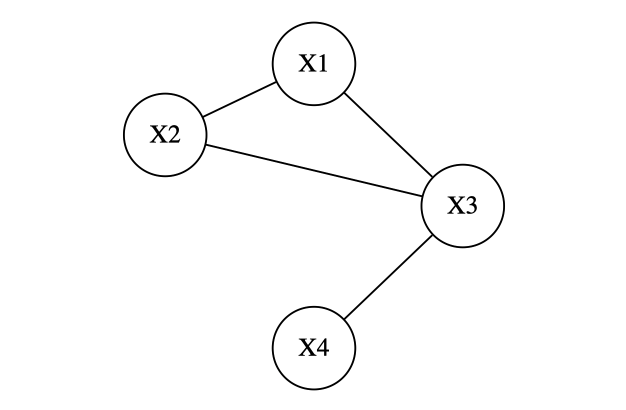
上記の2つの条件付き独立状態は1つにまとめることができます。
(X_1,X_2) \parallel X_4 \mid X_3 \\
因数分解基準により、4つの確率変数の同時分布は2つの関数の形に分化することがきます。
f(x_1,x_2,x_3,x_4)=g(x_1,x_2,x_3)h(x_3,x_4)
この二つの関数の変数は、無向グラフにおけるクリークを形成する頂点に対応しています。
有向独立グラフ
辺に方向性がある場合、有効独立グラフと呼びます。
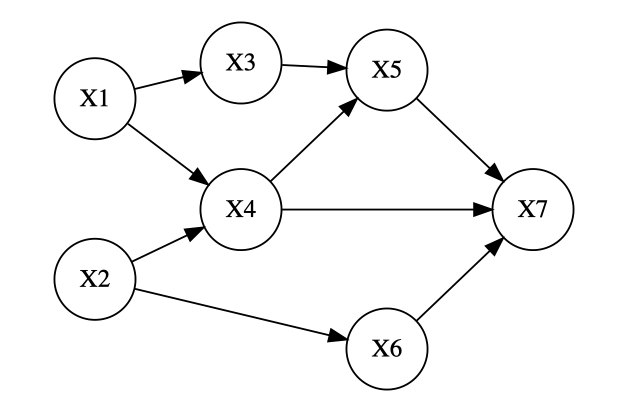
次のようなグラフをさします。
矢印が出て行く頂点は親、頂点が入って行く頂点を子と呼ばれます。
同時密度関数は条件付き分布と周辺分布との積に因数分解することができます。
各条件付き密度関数は、親に対応する変数が条件付けした、子となる変数の密度関数となる。
周辺密度関数の確率変数は、親がない頂点に対応しています。
f(x_1,x_2, ,x_7)=f(x_7 \mid x_4,x_5,x_6)f(x_6 \mid x_2)f(x_5 \mid x_3,x_4)f(x_4 \mid x_1,x_2)f(x_3 \mid x_1)f(x_2)f(x_1)
このような分解を逐次的因数分解と呼ばれる。
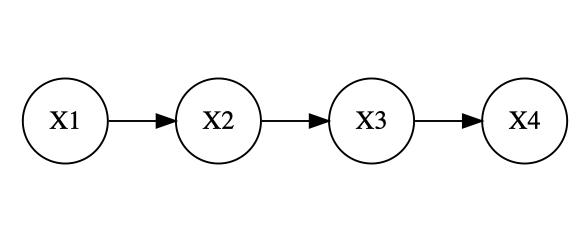
有効独立グラフが次のような直列形の時、条件付き確率密度関数は次のように分解することができる。
f(x_1,x_2,x_3,x_4)=f(x_4 \mid x_1, x_2,x_3)f(x_3 \mid x_1,x_2)f(x_2 \mid x_1)f(x_1)
有向独立グラフと無向独立グラフの関係
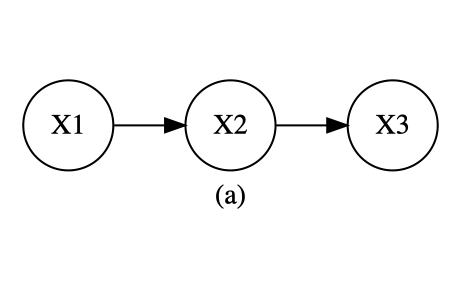
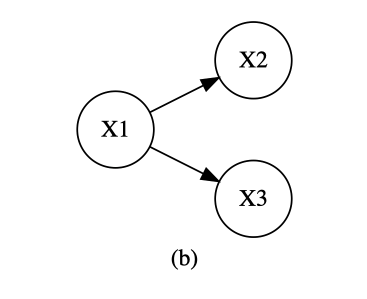
3つの頂点から構成される次の3つの有向独立グラフについて検討する。
 |
 |
 |
|---|
矢印の矢を取り除いて、形式的に無向独立グラフを作成した場合の独立関係は、次のようになる。
X_1 \parallel X_3 \mid X_2\\
X_2 \parallel X_3 \mid X_1\\
X_1 \parallel X_2 \mid X_3
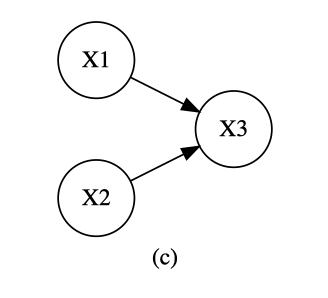
しかし、有向独立グラフにおいては(a)(b)は成立するが、(c)は成立しない。
(a)と(b)の同時密度関数は次のように因数分解でき、因数分解基準を満たしている。
f(x_1,x_2,x_3)=f(x_3 \mid x_2)f(x_2 \mid x_1)f(x_1)=g(x_2,x_3)h(x_1,x_2)\\
f(x_1,x_2,x_3)=f(x_3 \mid x_1)f(x_2 \mid x_1)f(x_1)=g(x_1,x_3)h(x_1,x_2)
一方で、次のように(c)を因数分解すると$f(x_3 \mid x_1,x_2)$は、$x_1,x_2,x_3$の関数であるため、因数分解基準を満たさず、条件付き独立関係はない。
f(x_1,x_2,x_3)=f(x_3 \mid x_1,x_2)f(x_2)f(x_1)
マルコフ性
局所的マルコフ性
大域的マルコフ性
グラフィカルモデル
多次元量的データにおいて、いくつかの変数間に条件付き独立関係から無向グラフを作成する構造モデルをグラフィカルモデルと呼ぶ。
変数間の関係は偏相関関係で定義し、偏相関が0ではない変数間に対応する無向グラフの辺が存在する。
次のような相関行列が成り立つ3変数があったとします。
\begin{array}{rrrr}
X_1 & 1.00& & \\
X_2 & 0.80 & 1.00 & \\
X_3 & 0.70 & 0.60 & 1.00
\end{array}
この相関行列に対して偏相関行列を求めます。
\begin{array}{rrrr}
X_1 &- & & \\
X_2 & 0.67 & - & \\
X_3 & 0.46 & 0.09 & -
\end{array}
これを元に生成される無向グラフは次のような形となる。
共分散選択
上記の偏相関係数において、$r_{23,1}$は非常に小さいため、$r_{23,1}=0.0$にします。
この時の無向グラフは次のようになる。
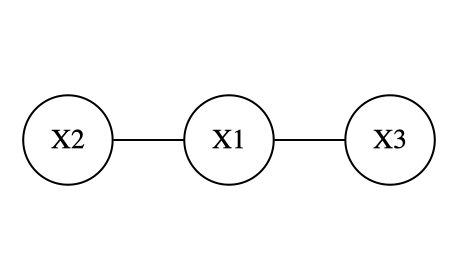
このように偏相関係数のいくつかを0とおいた相関構造モデルを求めるものが共分散選択です。
手順
どの偏相関係数を0にするかはデータから判断しなければなりません。
全ての偏相関係数を0に置換指定ないモデルをフルモデルとし、一度に偏相関係数を0にする箇所は1箇所のみとします。
偏相関係数を0に置換する場所の決定には、逸脱度またはAICに基づいて行います。
最も編相関係数が小さい係数を0に置換し、逸脱度かAICを求めます。
これを繰り返していき逸脱度かAICが改善しなくなったら、最適なモデルとが得られたとしてモデル選択を終了します。
逸脱度
共分散選択で採択された縮約モデル$RM$の逸脱度は次のように表すことができます。
dav(FM) = n \log \frac{\mid \hat \prod\mid}{\mid R \mid}
nは変数の数であり、Rは相関係数行列、$\hat \prod$は母相関係数の推定値を表ている。
また、$\mid・\mid$は行列式を表す。
Rで共分散選択
弁護士による合州国最高裁判事の評価データであるUSJudgeRatingsを利用して分析をしてみます。
USJudgeRatingsにおける変数の意味は次のようなものです。
| 変数名 | |
|---|---|
| CONT | 弁護士の判事との接触回数 |
| INTG | 裁判官としての誠実さ |
| DMNR | 態度 |
| DILG | 勤勉さ |
| CFMG | 裁判の流れの処理 |
| DECI | 敏速な決定 |
| PREP | 公判への準備 |
| FAMI | 法律への知識 |
| ORAL | 言葉による裁定の健全さ |
| WRIT | 文章による裁定の健全さ |
| PHYS | 肉体的能力 |
| RTEN | 記憶に値する |
コードは@sbtseijiさんの記事を参考にさせてもらいました。
はじめにpairplotを行い、データの確認を簡単に行います。
rating <- USJudgeRatings %>% data.frame()
ggpairs(rating)
# 省略
# qgraph(cor(rating), edge.labels=T, minimum=.2)
library(dplyr)
library(qgraph)
library(GGally)
library(corpcor)
library(ggm)
cov_select<-function(model=x, cov=y, n.obs=0, AIC=0, cov_orig=NULL){
if(is.null(cov_orig)){cov_orig <- cov}
print(sprintf("AIC= %.4f", AIC ), quote=F)
# 偏相関行列を作成
pmat <- cov %>%
cov2cor() %>%
cor2pcor()
diag(pmat) <- 1
# 偏相関係数を絶対値に変換
amat<-abs(pmat)
# モデルの係数が0の箇所を無限大に
amat[which(model == 0)] <- Inf
# 偏相関の絶対値が最小の要素を0にした修正モデルを作成
ncov <- nrow(cov)
model_post <- matrix(rep(1,ncov^2), nrow=ncov, ncol=ncov)
model_post[which.min(amat)] <- 0
model_post <- model_post * t(model_post) * model
# モデルのフィットとAICの算出
f <- fitConGraph(model_post, cov_orig, n.obs)
AIC_post <- f$dev - 2*f$df
# モデルの適合度が最大になるまで反復
if (AIC_post<AIC){
Recall(model_post, f$Shat, n.obs, AIC = AIC_post, cov_orig = cov_orig)
}
# AICが最小と判断した場合
else{
diag(pmat) <- 1
pmat[which(model == 0)] <- 0.0
colnames(pmat) <- colnames(model)
rownames(pmat) <- colnames(model)
RMSEA<-sqrt(max(((f$dev-f$df)/(f$df*(nrow(cov_orig)-1))),0))
res<-c(AIC,RMSEA=RMSEA)
return(list(fit=res, model=model, covmat=pmat))
}
}
rating_cov<-cov(rating)
# 初期モデルとして全変数間に関係をもたせたモデルを作成
# g_model<-UG(~CONT*INTG*DMNR*DILG*CFMG*DECI*PREP*FAMI*ORAL*WRIT*PHYS*RTEN)
ncov <- ncol(rating)
model_post <- matrix(rep(1, ncov^2), nrow=ncov, ncol=ncov)
diag(model_post) <- 0
colnames(model_post) <- names(rating)
rownames(model_post) <- names(rating)
model <- cov_select(model_post, rating_cov, ncov)
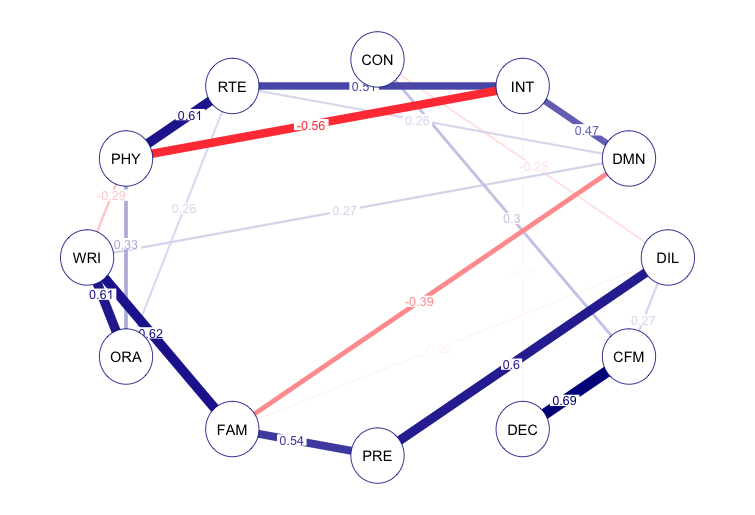
qgraph(model$covmat, edge.labels=T, minimum=.2,theme = "Borkulo")
CFMG:裁判の流れの処理をDECI:敏速な決定が最も正の相関が高いようです。
INTG:裁判官としての誠実さとPHYS:肉体的能力は、最も負の相関が高いようです。
また、裁判官としての誠実さと肉体的能力はそれぞれRTEN:記憶に値すると正の相関が少し高めです。
真面目な裁判官とタフな裁判官は、人望に厚くなり有名になりやすくなるのでしょうかね。
終わり
雑な感じに以上です。
次回は、グラフィカルlassoについてでもまとめたいと思います。