はじめに
積み本消化のために、Rで学ぶデータサイエンスシリーズのブートストラップ入門を読みましたので、まとめます。
近年、統計学の界隈ではp値の使用を禁止したり、乱用を減らしていこうという流れが大きくなってきています。
ブートストラップ法はその流れの中で使用することが推奨されるようになってきていると感じます。
久しぶりに統計学を勉強した感がありました。
#ブートストラップ法概要
母集団から標本集団が得られた時に、標本の平均値や分散等の統計量を算出し母集団の統計量$\theta$を推定します。
この時の推定は点推定であり、実際には不確実性があります。
また、その分布は未知の場合も多くあります。
この不確実性の程度をコンピュータ・シミュレーションによって見積もることができます。
その手法がブートストラップ法です。
ブートストラップ法は誤差推定,信頼区間の構成,仮説検定などに用いられます。
従来の複雑な数式に基づく理論を莫大な数値計算による単純なシミュレーションで置き換えるものであり、MCMCといったような推定とともに、計算機統計学と呼ばれる分野の手法です。
母集団の平均値を推定することを考えます。
はじめに標本集団$X=$ { $x_1,x_2,...,x_n$ }から、重複を許して$n$個(元のサンプルと同じ数)の標本を無作為に抽出します。$(i)$
これをブートストラップ標本$X^{*B}$と呼びます。
ブートストラップ標本毎に平均値を計算し、ブーストストラップ標本平均$\overline X^{*B}$を計算します。
この操作ををB回繰り返し、平均値$\overline X^{*B}$をB個作成することで、統計量の分布を得ることができるようになります。
そして、平均値を求めることにより、母集団の平均値$\theta$の推定値$\hat \theta$が得られます。
\hat \theta = \frac{1}{B} \sum_{b=1}^B \overline X^{\ast B}
この時の分布は、繰り返し回数を大きくすると中心極限定理により正規分布に収束します。
このようになリサンプリングを行うことで擬似的に母集団からの標本の抽出を行い、統計量の算出を行います。
また、分布を算出することができることから、統計量の真値が取りうる範囲である信頼区間を算出することもできます。
なお、リサンプリングする数$n$を様々な数にしてリサンプリングするマルチスケール・ブートストラップ法もあります。
通常のブートストラップ法よりも精度が高い推定を行うことができるとされています。
Rによるブートストラップ法
Rでブートストラップ法を行なって平均値の信頼区間を推定したいと思います。
いい感じのデータセットがなかったので、みんな大好きアヤメのデータです。
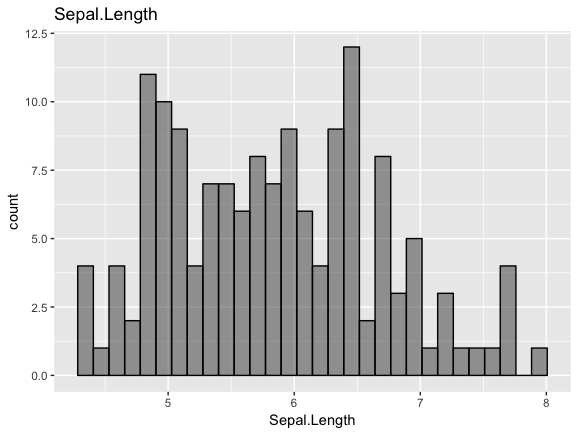
改めてになりますが、データを確認します
# データの確認
gp <- ggplot(iris, aes(x = Sepal.Length,alpha=0.8)) +
geom_histogram(bins = 30, color='black') +
ggtitle("Sepal.Length") +
theme(legend.position = 'none')
gp
2000個のブートストラップ標本を作成します。
set.seed(42)
# 2000回のブートストラップ平均の生成
N = 2000
mean_boot <- numeric(N)
for (k in 1:N){
strap_ind <- sample(1:150, replace = TRUE)
strap_dat <- iris$Sepal.Length[strap_ind]
mean_boot[k] <- mean(strap_dat)
}
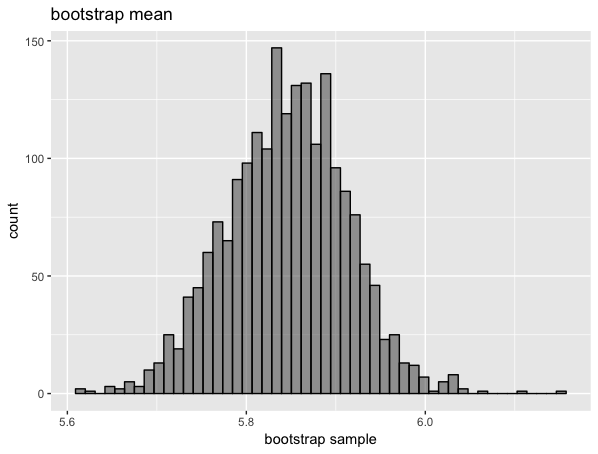
結果の分散と分布を確認してみます。
var(mean_boot)
# [1] 0.004483655
plot_bootstrap_hist <- function(bootstrap_sample, title = "bootstrap mean"){
gp <- bootstrap_sample %>%
as.data.frame %>%
ggplot(aes(x = .,alpha=0.8)) +
geom_histogram(bins = 50, color='black') +
theme(legend.position = 'none')+
ggtitle(title) +
xlab("bootstrap sample")
gp
}
plot_bootstrap_hist(mean_boot)
そして、両側95%信頼区間の算出を確認しまします。
# 両側95%信頼区間の算出
sort(mean_boot)[c(0.025*N, 0.975*N)]
# [1] 5.712667 5.971333
95%の確率でiris$Sepal.Lengthの平均値は5.713 ~ 5.971に含まれていると推定できます。
なお、この計算はbootパッケージを利用すると比較的簡単に作成できます。
bootパッケージでは統計量を算出する関数を作成する必要があります。
# bootパッケージを使う
library(tidyverse)
library(boot)
# 統計量を算出する関数を定義
my_mean <- function(d, i){
b <- d[i,]
mean(b$Sepal.Length)
}
ratio.boot <- boot(iris, statistic = my_mean, R=2000, stype = "i")
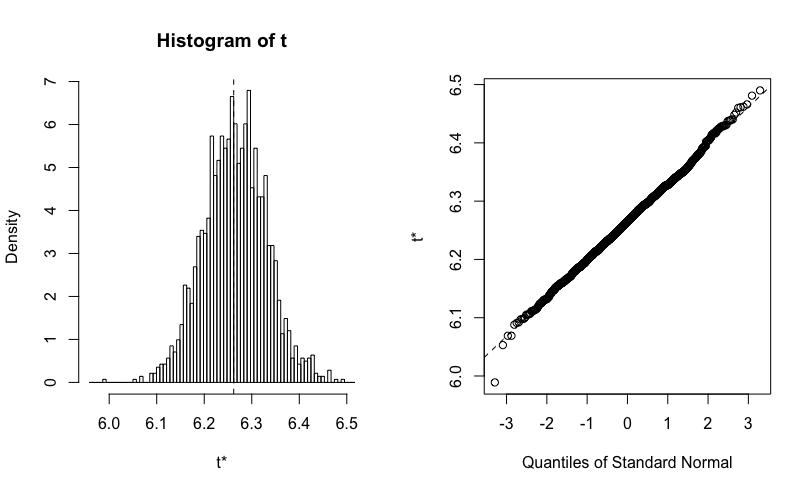
ratio.boot %>% plot
そして、結果のオブジェクトを確認すると、推定される平均値におけるバイアスと分散を確認することができます。
バイアスは次のように定義されている推定された偏りです。
\hat bais(\theta) = \frac{1}{B}\sum_{b=1}^B \theta^{\ast b}-\hat \theta
分散は次にように定義されているブートストラップ分散推定です。
\hat var(\theta) = \frac{1}{B-1}\sum_{b=1}^B (\theta^{\ast b}-\hat \theta)^2
> ratio.boot
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = iris, statistic = my_mean, R = 2000, stype = "i")
Bootstrap Statistics :
original bias std. error
t1* 5.843333 0.001987667 0.06856637
推定量の精度のブートストラップ推定
ブートストラップ法は、大きく分けて二種類の手法があります。
パラメトリック・ブートストラップ法とノンパラメトリック・ブートストラップ法です。
パラメトリック・ブートストラップ法
パラメトリック・ブートストラップ法は、ブートストラップ標本から得られるパラメータで定義される分布$F$を仮定し、信頼区間を求めたり分析を行なっていく手法です。
信頼区間を推定する際には、平均が正規分布に従っていると改定し、ブートストラップ標本から分散を算出し用います。
ノンパラメトリック・ブートストラップ法
ノンパラメトリック・ブートストラップ法は、得られたブートストラップ標本の経験分布$F$を用いて、信頼区間を求めたり分析を行なっていく手法です。
信頼区間を推定する際には、ブートストラップ標本の上位/下位$\alpha$%を算出して用います。
ジャックナイフ分散推定
ブートストラップ法と同様に再標本化により統計量の推定を行う手法にジャックナイフ法があります。
ジャックナイフ法では、特定の標本$x_i$を除いたN-1個の標本を用いて再標本化を行います。
leave-one-out (LOO) クロスバリデーションとも呼ばれています。
ジャックナイフ法は、$\hat \theta$の分散の推定を行うことが多いです。
リサンプリングした標本の平均値$\hat \theta_{(i)}$とすると、ジャックナイフ法による分散は次のように求めることができる。
\sigma_J^2 = \frac{n-1}{n} \sum^n_{i-1}(\hat \theta_{(i)}-\hat \theta_{(\cdot)})^2
$\hat \theta_{(i)}$は$y_i$を取り除いた時の推定量(平均値)である。また、$\hat \theta_{(\ast)}$は平均値である。
\hat \theta_{(\cdot)} = \frac{1}{n}\sum^n_{i=1} \hat \theta_{(i)}
Rでジャックナイフ分散推定を行い、ブートストラップ標本の分散推定を行なってみます。
# ジャックナイフ推定量の関数
jack_var <- function(x){
n <- length(x)
theta <- numeric(n)
for (i in 1:n){
theta[i] <- mean(x[-i])
}
return((n-1)^2/n*var(theta))
}
# ジャックナイフ分散推定
jack_var(iris$Sepal.Length)
# [1] 0.00457129
様々信頼区間の推定
ブートストラップ法を用いることの主眼は、推定値の不確実性である分散を推定することにあります。
分散を推定することにより、得られている標本から推定される統計量をどれほど信頼して良いのかがわかり、意思決定の場面で役立つと思われます。
信頼区間の推定には様々な手法が存在し、ここではテキストで紹介されていたものを紹介します。
標準信頼区間
パラメトリック・ブートストラップ法の基本的なものです。
ブートストラップ標本における分散を求め、推定される統計量$\hat \theta$のバラツキとします。
###アルゴリズム
- $\hat \theta^{\ast 1}$ ,..., $\hat \theta^{\ast B}$の標準偏差$\hat \sigma$を求める
- $N(1,0)$の下側$100p$%点 (0 < p < 1) を$z(p)$と表し, この値を$p=1− \alpha/2$に対して求めておく。
- $\theta$の$100(1-\alpha)$%両側信頼区間は次式で得られる。
[\theta - z^{(1-\alpha/2)} \hat \sigma , \theta + z^{(1-\alpha/2)} \hat \sigma]
###Rで標準信頼区間
# 2000回のブートストラップ平均の生成
set.seed(42)
N = 2000
mean_boot <- numeric(N)
for (k in 1:N){
strap_ind <- sample(1:150, replace = TRUE)
strap_dat <- iris$Sepal.Length[strap_ind]
mean_boot[k] <- mean(strap_dat)
}
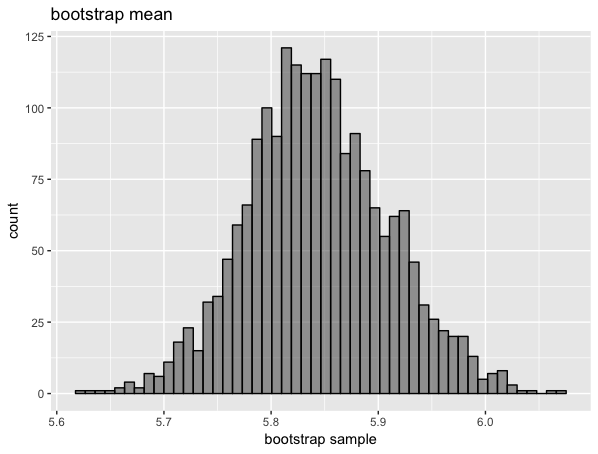
plot_bootstrap_hist(mean_boot)
# 両側95%信頼区間の算出
theta_sd <- sd(mean_boot)
theta_mean <- mean(iris$Sepal.Length)
c(theta_mean - 1.96*theta_sd, theta_mean + 1.96*theta_sd)
# [1] 5.714065 5.972602
##パーセンタイル信頼区間
分布を仮定せず行うノンパラメトリック信頼区間の推定方法であり、冒頭で行なった信頼区間の算出方法と同じです。
###アルゴリズム
- $\hat \theta^{*1}$,...,$\hat \theta^{*B}$を小さい順にソートする.
- $0<p<1$に対して$pB$番目に小さい数値を^(p)と表す。$pB$が整数値でなければ、となりあう値を線形補間する。
- $p=\alpha/2$および$p=1-\alpha/2$とおいて,$100(1-\alpha)$%両側信頼区間は次式で与える。
[\hat \theta^{*(\alpha/2)}, \hat \theta^{*(1-\alpha/2)}]
$\alpha$の95%信頼区間は次にように表現できる。
[\hat \theta^{*(0.025)}, \hat \theta^{*(0.975)dxx}]
# 両側95%信頼区間の算出
sort(mean_boot)[c(0.025*N, 0.975*N)]
# [1] 5.717333 5.977333
##ブートストラップ-t法
ブーストストラップ信頼区間は$\hat \theta -\theta$の分布を$\hat \theta^{*} -\hat \theta$で近似しています。
真の分布関数Fと経験分布$\hat F_n$での分布のずれが顕著な場合は、ブーストストラップ信頼区間の精度は悪くなってしまいます。
これを解消するために$\hat \theta -\theta$ではなく、$T=(\hat \theta -\theta)/ \hat \sigma$の分布で考えます。
ここで$\hat \sigma^2$は$\hat \theta$の分散に対する推定量です。
$\alpha, 1-\alpha$分位点を$u_\alpha, u_{1-\alpha}$とすると次にような式が成り立ちます。
1-2\alpha = Pr \left[ u_\alpha \le \frac{\hat \theta -\theta}{\hat \sigma} \le u_{1-\alpha} \right]
= Pr \left[\hat \theta -\hat \sigma u_\alpha \le \theta \le \hat \theta -\hat \sigma u_{1-\alpha} \right]
各分位点$u_\alpha, u_{1-\alpha}$を$T^\ast=(\hat \theta^\ast -\theta^\ast)/ \hat \sigma^\ast$の分位点$T^\ast_{(B \alpha)}, T^\ast_{(B(1-\alpha))}$で近似すれば、次のようなブートストラップ-t信頼区間を得ることができます。
(\hat \theta- \hat T^\ast_{(B \alpha)},\hat \theta- \hat T^\ast_{(B(1-\alpha))})
$T^{\ast}$を計算する際に$\hat \sigma^{\ast}$は、ノンパラメトリックの場合ジャックナイフ法を用いて推定します。
なお、ブートストラップ-t信頼区間は信頼区間の幅が広くなってしまう傾向があることが知られています。
###アルゴリズム
1.次のように$\hat \theta^{* }$を標準化したブートストラップ標本 $\hat t^{*1} ,..., \hat t^{*B}$ を取得する。
t^* =\frac{\hat \theta^{*}-\hat \theta}{\hat \sigma^{*}}
2.$\hat t^{*1}$ ,..., $\hat t^{*B}$を小さい順にソートする
3.$t^\ast$のブートストラップ分布の両側$100(1-\alpha)$%点,すなわち$t^{\ast (1-\alpha/2)}$を計算する.
4.信頼水準$1-\alpha$の両側信頼区間を次式で与える.
[\theta - t^{\ast (1-\alpha/2)} \hat \sigma , \theta + t^{\ast (1-\alpha/2)} \hat \sigma]
###Rでブートストラップ-t信頼区間を算出
# ブートストラップ-t信頼区間 ----------------------------------------------------------
N = 2000
m <- mean(iris$Sepal.Length)
mean_boot <- numeric(N)
for (i in 1:N){
y <- sample(iris$Sepal.Length, replace = TRUE)
mean_boot[i] <- (mean(y)-m)
mean_boot[i] <- mean_boot[i]/sqrt(jack_var(y))
}
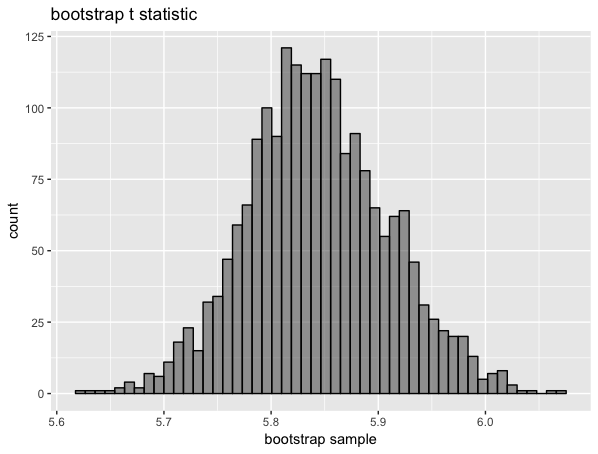
ブートストラップ標本の分布を見てみます。
plot_bootstrap_hist(mean_boot, "bootstrap t statistic")
# 信頼区間の算出
m - sqrt(jack_var(iris$Sepal.Length))*sort(mean_boot)[N*0.975]
> [1] 5.717164
m - sqrt(jack_var(iris$Sepal.Length))*sort(mean_boot)[N*0.025]
> [1] 5.975721
この精度を改善するためにいくつかの手法が存在し、テキストでは次にような信頼区間推定手法を紹介していました。
##分散安定化変換による信頼区間
推定量$\hat \theta$の分布は一般$n$にはパラメータ$\theta$に依存しているが、$var(\hat \theta)$が$\theta$に強く依存している場合があります。
分散に依存しない状態に標本を変換することにより、信頼区間の推定精度が大きく改善することがあります。
分散化安定化変換を$\xi =h(\theta)$とする。この関数はデータによって異なり適切なものを選択する必要がある。
変換後のパラメータ$\xi$に対する$100(1-2\alpha)$%信頼区間は次のようになる。
(h(\hat \theta)-U^{\ast}_{(B(1-\alpha))}, h(\hat \theta)-U^{\ast}_{(B \alpha)}) = (2h(\hat \theta)-h(\hat \theta^{\ast}_{(B(1-\alpha))}), 2h(\hat \theta)-h(\hat \theta^{\ast}_{(B \alpha)}))
この信頼区間に対して、$h$の逆変換を行うと$\theta$の信頼区間が求まります。
###アルゴリズム
- $\hat \theta^{\ast}$に分散化安定化変換を行なったブートストラップ標本 $\hat \xi^{\ast 1} ,..., \hat \xi^{\ast B}$ を取得する。
- $\hat \xi^{\ast 1}$ ,..., $\hat \xi^{\ast B}$を小さい順にソートする
- $\hat \xi^\ast$のブートストラップ分布の下側$100(1-\alpha)$%点、すなわち$\hat \xi^{\ast (1-\alpha)}$を計算する.
- 信頼水準$1-\alpha$の上側信頼区間の下限を次式で与える.
[2h(\hat \theta)-\xi^{\ast (1-\alpha)}, 2h(\hat \theta)-\xi^{\ast (1-\alpha)}]
###Rで分散安定化変換による信頼区間の算出
ブートストラップ標本の平均値が分散に依存していないかを確認するために、両者の関係を可視化してみます。
mean_boot_org <- numeric(N)
var_boot_org <- numeric(N)
for (i in 1:N){
y <- sample(iris$Petal.Length, replace = TRUE)
mean_boot_org[i] <- mean(y)
var_boot_org[i] <- jack_var(y)
}
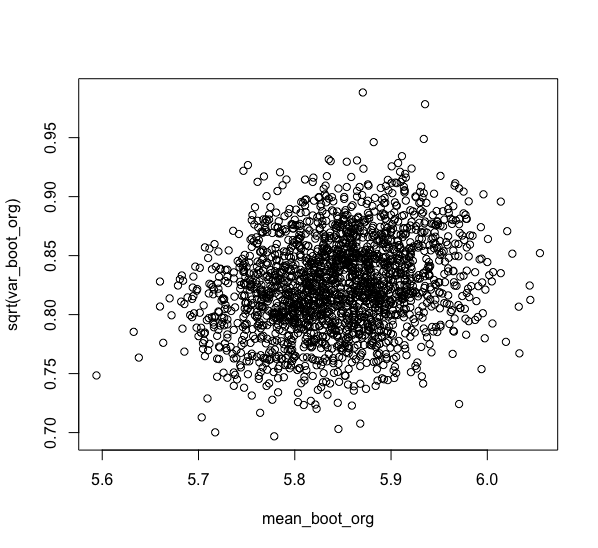
plot(mean_boot_org, sqrt(var_boot_org))
平均値と分散は弱く依存していそうです。
ブートストラップ標本の平均値を対数変換した値と分散の関係を可視化してみます。
stat_func <- function(x){log(mean(x))}
mean_boot <- numeric(N)
var_boot <- numeric(N)
for (i in 1:N){
y <- sample(iris$Petal.Length, replace = TRUE)
mean_boot[i] <- stat_func(y)
var_boot[i] <- jack(y, stat_func)
}
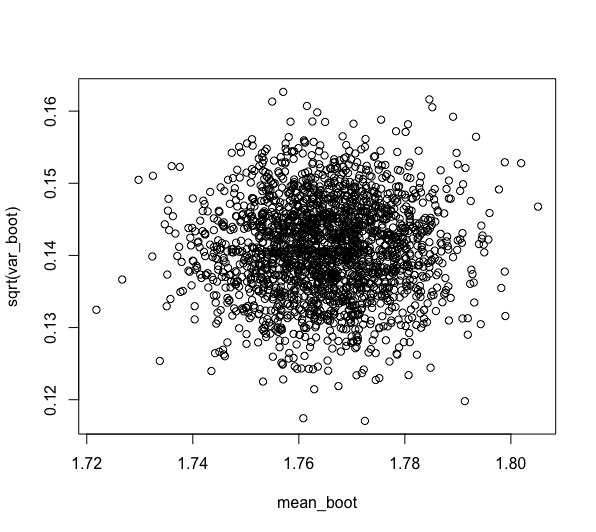
plot(mean_boot, sqrt(var_boot))
平均値と分散は依存しない状態になったと考えられます。
それでは、ノンパラメトリックブートストラップ-t信頼区間を算出してみます。
var_boot <- numeric(N)
for (i in 1:N){
y <- sample(iris$Petal.Length, replace = TRUE)
var_boot[i] <- stat_func(y)-log(m)
}
l <- log(m) - sort(var_boot)[N*0.975]
e <- log(m) - sort(var_boot)[N*0.025]
exp(c(l,e))
# [1] 5.712975 5.979082
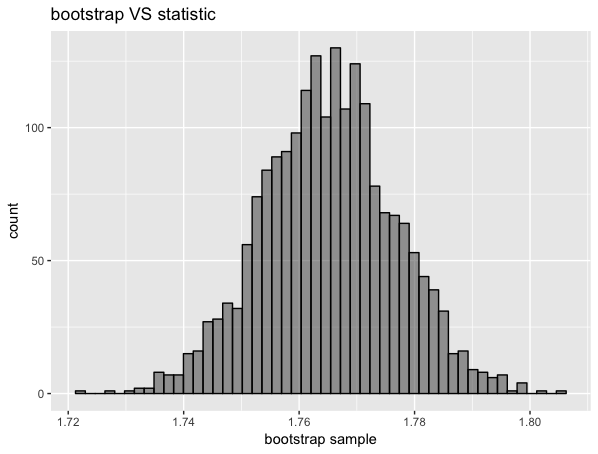
ブートストラップサンプリングの分布をみてみます。
plot_bootstrap_hist(mean_boot, "bootstrap VS statistic")
####パッケージによる推定
分散安定化変換を用いたブートストラップ法はbootパッケージでも実装可能です。
はじめに分散安定化変換を行なった場合です。
# bootstrapパッケージによる推定
library(bootstrap)
library(boot)
res <- boott(iris$Sepal.Length, mean, prec=c(0.025,0.975), nboott = N)
res$confpoints[c(3,9)]
# [1] 5.695290 5.991252
VS引数をTrueとすると分散化安定化変換を行なった信頼区間の推定が行えます。
res.vs <- boott(iris$Sepal.Length, mean, prec=c(0.025,0.975), VS = TRUE, nboott = N)
res.vs$confpoints[c(3,9)]
# [1] 5.721673 5.982693
##BCa法
分散化安定化変換を用いる場合には、次式が成り立つとして信頼区間を推定しています。
Pr[h(\hat \theta)-h(\theta) \le u_\alpha] = Pr[h(\hat \theta)-h(\theta) \ge - u_\alpha]
しかし、この性質は厳密に満たす変換は一般に存在しない。また、存在しても$h$が分散安定化変換担っているとは限らないです。
そのため、パラメータ$\theta$を$\xi = h(\theta)$と変換し、未知の関数$h$が次式を満たすと仮定します。
\hat \xi = h(\hat \theta) \sim N(\xi-\omega \sigma (\xi), \sigma^2 (\xi))
ここで、$\sigma(\xi)=1+a \xi$、$\omega$は偏り修正定数、$a$は定数である。
そして、$\omega$と$a$は推定すべき定数です。
$a$は次の式で表現できます。
a=Pr \left[ \frac{\hat \xi - \xi+\omega \sigma (\xi)}{\sigma(\xi)}\geq z_{1-\alpha} \right]
=Pr \left[ \frac{\hat \xi - \xi+\omega \sigma (\xi)}{\sigma(\xi)}\geq z_{1-\alpha} \right]
ノンパラメトリックモデルの場合、ジャックナイフ方をを用いて次のように推定することができます。
\hat a = \frac{1}{6} \frac{\sum^n_{i=1} (\hat \theta_{(\cdot)}-\hat \theta_{(i)})^3}{ \left \{ \sum^n_{i=1} \hat \theta_{(\cdot)}-\hat \theta_{(i)})^2 \right \}^{3/2}}
$\omega$は次のように推定されます。
\omega = \Phi^{-1} \left\{ Pr_\ast [\hat \theta^\ast \leq \theta] \right\}
これをB回のブートストラップ・シミュレーションを行い推定します。
\hat \omega = \Phi^{-1} \left( \frac{1}{B} \sum^B_{b=1}I \{\hat \theta^\ast \leq \theta \} \right)
###アルゴリズム
1.事象が成立した回数を #{·} と書いて、$\hat \alpha_0$を計算する。
\hat \alpha_0=\frac{\# \{ \theta^{\ast b} \le \hat \theta ,b=1, \cdots , B \}}
{B}
および、$z^0 = z^{\hat \alpha_0}$を計算する。
2.$X$から要素$x_i$を取り除いて計算した$\hat \theta$を$\hat \theta (i) $とし、次式に従い加速定数$a$と$\omega$を次式で推定する。
\hat a = \frac{1}{6} \frac{\sum^n_{i=1} (\hat \theta_{(\cdot)}-\hat \theta_{(i)})^3}{ \left \{ \sum^n_{i=1} \hat \theta_{(\cdot)}-\hat \theta_{(i)})^2 \right \}^{3/2}}
\hat \omega = \Phi^{-1} \left( \frac{1}{B} \sum^B_{b=1}I \{\hat \theta^\ast \leq \theta \} \right)
3.$X \backsim N(0, 1)$ の累積分布関数を $\Phi (x)$ とし. 次の量を計算する。
\hat \alpha = \Phi \left \{ \omega + \frac{\omega + z_{\alpha}}{1-a(\omega+z_{\alpha})} \right \}
4.信頼水準 1 − α の両側信頼区間を次式で求める。
[\hat \theta^{\ast \hat \alpha}, \hat \theta^{\ast (1-\hat \alpha)}]
###RでBCa法による信頼区間の算出
# 定数aを推定する関数
a <- function(x ,stat){
n <- length(x)
theta <- numeric(n)
for (i in 1:n) {theta[i] <- stat(x[-i])}
theta.dot <- mean(theta)
nu <- sum((theta.dot-theta)^3)
de <- (sum((theta.dot - theta)^2))-(3/2)
return(nu/(6*de))
}
# 順位を計算する関数
order <- function(alpha, a.h){
d <- w + qnorm(alpha)
alha.h <- pnorm(w+d/(1-a.h*d))
round(B*alha.h)
}
リサンプリングを行い信頼区間の推定を行います。
y <- iris$Sepal.Length
N <- 2000
theta <- numeric(N)
for(b in 1:N){
y.b <- sample(y, replace = TRUE)
theta[b] <- mean(y.b)
}
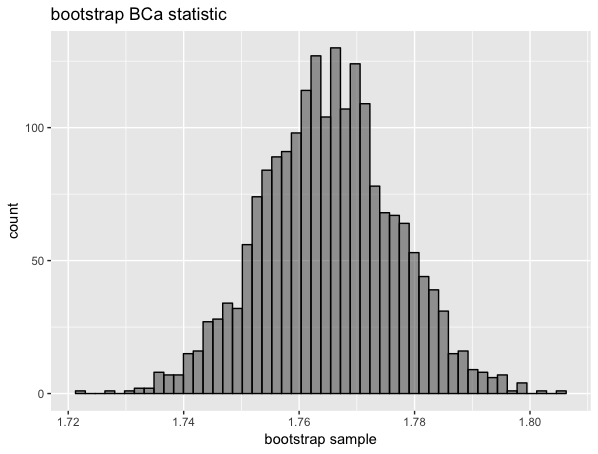
plot_bootstrap_hist(mean_boot, "bootstrap BCa statistic")
w <- qnorm(sum(theta<=mean(y))/N)
a.h <- a(y, mean)
limit <- order(c(0.025, 0.975), a.h)
sort(theta)[limit]
# [1] 5.708000 5.975333
#終わり
ブートストラップ法の概要と信頼区間を算出するアルゴリズムについて紹介しました。
次は、本題のブートストラップ法を仮説検定や回帰分析に適用する方法をまとめたいと思います。