はじめに
昨日行われて統計数理研究所主催のリーディングDAT講座「地理情報と空間モデリング」に参加してきました。
GPSデータや気象データ、地下データといった位置が意味を持つデータを活かした統計モデリングを学んできました。
復習も兼ねて重要な部分をまとめて、Rでモデリングをおこないたいと思います。
地理空間データについて
次のようなデータを地理空間データと呼びます。
- 国勢情報
- 土地情報
- 衛星画像
- 携帯端末のGPSデータ
- 気象データ
近年これらのデータは非常に増えてきています。
また、地球科学や生態学、計量経済学といった様々な分野で利用されています。
それぞれの分野で地理空間データの特性を加味したり活かしたりながらモデリング/分析を行なっています。
地理空間データの特性とは、次にような特性が挙げられます。特に上二つが重要のようです。
| 特徴 | 概要 |
|---|---|
| 空間相関 | 標本は独立ではなく、地理的に隣接するほど体外に相関 |
| 空間異質性 | 地域によって標本特性が変化 |
| 空間交絡 | 各変数が空間的なパターンを持つ |
| 不確実性 | 希少イベントの集計データなどは、ノイズが乗っていることが多い |
Rで空間データのプロット
空間データは、spパッケージで提供されているSpatialPolygonsDataFrameクラスで扱ってきます。
SpatialPolygonsDataFrameクラスのデータ操作方法について、あまり理解できていませんので、講師の人のコードをそのままという感じです。悪しからず。
プロットは、spplot関数で描写ができ、対象の値を何段階で色分けし、どの色コードを割り当てるのかを指定する必要があるようです。
色コードの割り当てはRColorBrewer::brewer.palでいい感じにできるようです。
library(rgeos)
library(rgdal)
library(RColorBrewer)
library(NipponMap)
library(spdep)
geo_data <- readOGR(system.file("shapes/jpn.dbf", package="NipponMap")) # 都道府県データを読み込み
proj4string(geo_data) <- "+proj=longlat +ellps=WGS84 +datum=WGS84"
geo_data <- spTransform(geo_data, CRS=CRS("+init=epsg:2451 +units=km")) # 単位の設定
geo_data@data$area <- gArea(geo_data, byid=TRUE) # 各都道府県の面積を評価
geo_data@data$population <- as.numeric(as.character(geo_data@data$population))
geo_data@data$popden <- geo_data@data$population/geo_data@data$area # 人口密度を評価
names(geo_data)[3] <- "PREF" # 3行目の列名を"PREF"にする
nc <- 8 # 色分け数を指定
cols <- brewer.pal(n = nc, name = "YlOrRd") # 色コードの配列を作成
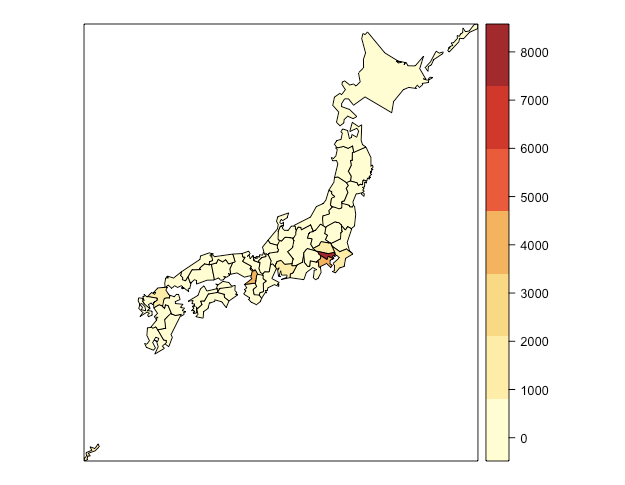
spplot(geo_data, "popden", cuts = nc-2, col.regions = cols) # 色分けした地図を作製
まぁ、東京が斗出して人口多いですよね。
空間相関
立地的に隣接しているポイントのデータは互いに相関関係にあります。
正の相関は、ある自治体で税率を上げたときに、次に期に隣り合った自治体が税率をあげるような空間的な波及がある場合に生まれます。
負の相関は、大型店がある地域では売り上げが高く、周辺の地域の小規模点しかなく売り上げた低くなってしますような、空間競争がある場合に生まれやすいです。
空間相関はモランI統計量と呼ばれる指標で表現され、次式で定義されます。
I = \frac{n}{\sum_i \sum_j w_{ij}}\frac{\sum_i \sum_j w_{ij}(y_j-\bar y)(y_i-\bar y)}{\sum_i (y_i-\bar y)^2}
ここで、$y_i$はi番目の標本、$\bar y$は標本平均、nは標本数です。
また、前半の分数部分は補正項です。
Rではspdep::noran.testで求めることができます
> listw <- geo_data %>%
+ coordinates %>%
+ knearneigh(4) %>%
+ knn2nb() %>%
+ nb2listw
> moran <- moran.test(geo_data$popden, listw=listw) # 人口密度(popden)のモランI統計量
> print(moran)
Moran I test under randomisation
data: geo_data$popden
weights: listw
Moran I statistic standard deviate = 2.9682, p-value = 0.001498
alternative hypothesis: greater
sample estimates:
Moran I statistic Expectation Variance
0.190576136 -0.021739130 0.005116457
この関数は、得られたモランI統計量の有意性の検定を行うものであり、p-valueを用いると検定が行えます。
また、注目点と周辺の相関を評価するローカルモランI推定量もあります
I_i = \frac{1}{m} (y_i-\bar y) \sum_{j=0}^J w_{ij}(y_j-\bar y)
ここで先頭の分数部分は補正項です。
Rではlocalmoran関数で求まります。
> lmoran <- localmoran(geo_data$popden,listw=listw) # 人口密度(popden)のローカルモランI統計量
> head(lmoran) # lmoranの最初の数行
Ii E.Ii Var.Ii Z.Ii Pr(z > 0)
1 0.1860348 -0.02173913 0.1478095 0.5404305 0.2944501
2 0.1685270 -0.02173913 0.1478095 0.4948918 0.3103382
3 0.1789829 -0.02173913 0.1478095 0.5220882 0.3008045
4 0.1225235 -0.02173913 0.1478095 0.3752345 0.3537430
5 0.1785888 -0.02173913 0.1478095 0.5210632 0.3011614
6 0.1620714 -0.02173913 0.1478095 0.4781005 0.3162893
ローカルモランI統計量の分布を見てみましょう。
geo_data$lmoran <- lmoran[, "Z.Ii"] # ローカルモランI
geo_data$lmoran_p <- lmoran[, "Pr(z > 0)"] # ローカルモランIのP値
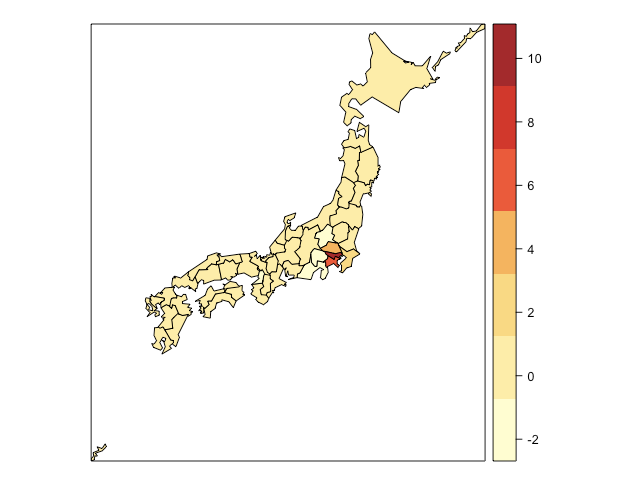
spplot(geo_data, "lmoran", cuts = nc-2, col.regions = cols) # ローカルモランI統計量の分布
東京は周辺との相関が大きいようです。一方で、大阪は負の相関あるようです。これは大阪のみ人口密度が周辺の府県より高いためだと言えます。
ICARモデル
空間疫学や生態額では、ノイズが多いデータであったり、1領域内の標本が十分に得られないような不確実性が高いことが多いです。
不確実性が高いデータでは、ある領域で正となるデータが多く得られた場合、偶然得られたのか、本当にそのようなデータが得られる要因があったのかがわかりにくくなってしまいます。
そのため、周辺の情報を顧慮して分析していきます。
具体的には、空間相関を事前分布として与え、各領域のデータへの当てはまりを尤度を高めるモデルを考えます。
ICARモデル
空間相関を表現する事前分布として、ICAR事前分布が考えられており、次のように定義されています。
z_i|z_{j=i} \sim N \left(\frac{\sum_j w_{ij}z_j}{\sum_j w_{ij}},\frac{\tau^2}{\sum_j w_{ij}}\right)
ここで、$w_{ij}$は周辺との関係を示す変数であり、周辺であると1、それ以外が0です。
また、$\tau^2$は精度パラメータです。
ガウス分布の期待値部分は周辺と似た値をとる=なめらかさを表現しており、分散部分はなめらかさの確からしさであり、大きくなるとなめらかさがなくなり、一様の値をとるようになり、小さくなるとなめらかさが強調されます。
潜在変数$z_i$から$y_i$への当てはまりは次のように表現されます。
y_i|z_i \sim N(z_i,\sigma^2)
上記の二式からなるモデルをICARモデルと呼ばれています。
ICARモデルをグラフィカルモデルで表現すると次のような感じです。

ICARモデルの特徴は3つ挙げられいました。
- 計算効率が良い
- 非ガウスモデリングと親和性が高い
- ベイズモデリングと親和性が高い
GLM+ICARモデル(ポアソンICARモデル)
ある領域の感染者数や動物の観測数はカウントデータであるため、ポアソン分布に従う可能性が高いです。
そのため、ICARモデルのデータ分布をガウス分布からポアソン分布を用いるGLMに拡張することで、モデルの表現力を増やすことができます。
ICARモデルの$y_i$への当てはまりの式をGLMに拡張します。
y_i \sim Poisson(\mu_i)\\
\mu_i = \alpha_i exp \left(\sum_{k=1}^K x_{ik}\beta_k+z_i \right)
ここで、$x_{ik}$は領域iのk番目の説明変数であり、$\beta_k$はその係数です。
$\beta_k$と$\tau^2$は事前分布をうまく指定することで、ベイズ推定を行うことができます。
RでGLM+ICARモデル
イギリスのグラスゴーの呼吸器疾患のデータに対して、モデルを適用します。
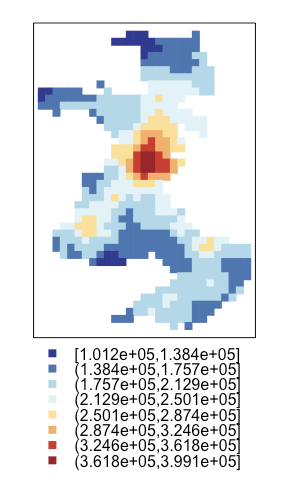
はじめに呼吸器疾患数のデータを可視化してみます。
# データの読み込みと可視化 ------------------------------------------------------------
data(GGHB.IG) # 住宅価格データ
data(pollutionhealthdata) # グラスゴーのゾーン別の呼吸器疾患の患者数データ
dat <- merge(x = GGHB.IG,
y = pollutionhealthdata,
by = "IG",
all.x = FALSE,
duplicateGeoms = TRUE)
# 患者数の可視化
nc <- 10 # 色分けのレベル数
cuts <- seq(0,220,len=nc+1)
cols <- rev(brewer.pal(n = nc, name = "RdYlBu")) #カラーコード配列を生成
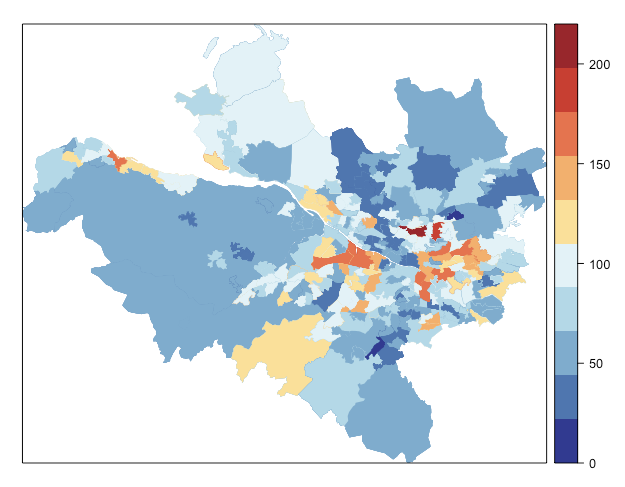
spplot(dat,
"observed",
col.regions = cols,
lwd = 0.01,
colorkey = list(at= cuts),
at = cuts,
col = "transparent")
次にICAR事前分布を仮定したモデリングを行います。
# GLM+ICARモデル -------------------------------------------------------------
W.nb <- poly2nb(spatial_data, row.names =rownames(spatial_data@data)) # 隣接の有無に基づく隣接行列
W <- nb2mat(W.nb, style="B") # 上記行列をWに出力
formula <- observed ~ offset(log(expected)) + pm10 + jsa
res_ICAR<- S.CARleroux(formula=formula, #MCMCによる推定
data=spatial_data@data,
family="poisson",
W = W,
rho = 1,
burnin = 3000,
n.sample = 10000)
結果を確認します。
> res_ICAR # 推定結果の確認
#################
#### Model fitted
#################
Likelihood model - Poisson (log link function)
Random effects model - Leroux CAR
Regression equation - observed ~ offset(log(expected)) + pm10 + jsa
Number of missing observations - 0
############
#### Results
############
Posterior quantities and DIC
Median 2.5% 97.5% n.sample % accept n.effective Geweke.diag
(Intercept) -1.0289 -1.1427 -0.8897 7000 42.6 120.5 -1.2
pm10 0.0377 0.0273 0.0465 7000 42.6 118.2 1.1
jsa 0.0812 0.0749 0.0875 7000 42.6 146.1 2.2
tau2 1.2194 1.1037 1.3515 7000 100.0 1869.6 0.5
rho 1.0000 1.0000 1.0000 NA NA NA NA
DIC = 10676.12 p.d = 1020.169 LMPL = -5593.75
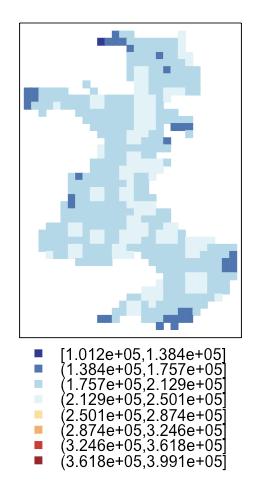
結果を可視化してみましょう。
# 結果の可視化
spatial_data@data$ICARfit <- res_ICAR$fitted.values
nc <- 10
cols <- rev(brewer.pal(n = nc, name = "RdYlBu"))
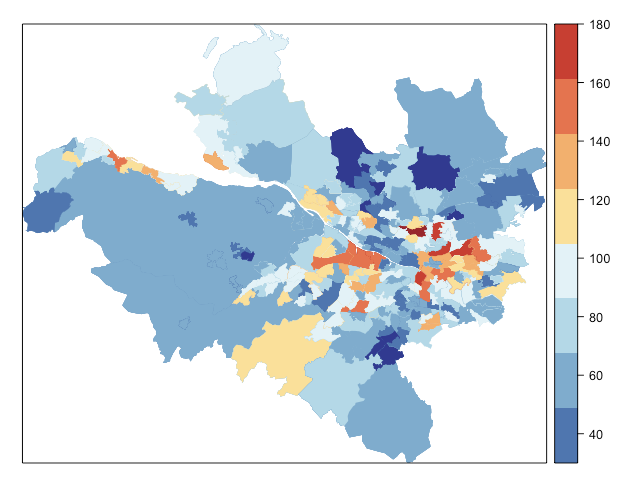
spplot(spatial_data, "ICARfit",
col.regions = cols,
col = "transparent",
colorkey = list(at= c(-Inf,seq(30,180,len=nc-1),Inf)),
at = c(-Inf,seq(30,180,len=nc-1),Inf))
色の割り当てが最初の図と同じにしたかったんですが、うまくいきませんでした。
それも相まってモデリングによる当てはまりがよくわからなくなってます...。
SARモデル
計量経済学の分野では説明変数を持ち、空間的な影響の波及を加味したモデルが経済学の理論と親和性が高く、支持されているそうです。
SARモデル
SARモデルは、観測値の空間的な影響の波及/空間相関を加味したモデルです。
y_i = \rho \sum_{j \neq i}^n w_{ij}y_i+\epsilon_i \\
\epsilon_i \sim N(0,\sigma^2)
SARモデルに説明変数を追加し、非説明変数が空間相関を持つモデルとしてSLM(Spatial lag model)が提案されています。
y_i = \rho \sum_{i\neq j}^n w_{ij}y_j + \sum_{k=1}^K \beta_k+\epsilon_i \\
\epsilon_i \sim N(0,\sigma^2)
ここで、$\rho$は空間相関の強さを表すパラメータです。
正の場合正の空間相関があり、負の場合は負の空間相関があります。
様々なモデル
SARモデルは観測値の空間的な波及を加味していますが、説明変数などの波及を加味したモデルが様々存在しています。
(派生モデルが多すぎて何をどう使えばいいのかが非常にわかりにくいという指摘もあるようです。)
- SLM(Spatial lag model):非説明変数が空間相関を持つ
- SLX(Spatial lag of X model):説明変数が空間相関を持つ
- SEM(Spatial error model):誤差項が空間相関を持つ
- SDM(Spatial Durbin model):非説明変数と説明変数が空間相関を持つ
- SDEM(Spatial Durbin error model):説明変数と誤差項が空間相関を持つ
- SACM(SARAR model):被説明変数と誤差項が空間相関を持つ
これらのモデルの推定では、2SLS(2-ste least squares)と呼ばれる OLSを二段階で適用することで空間相関の影響を排除したパラメータの推定ができるそうです。
しかし、一段階目のOLSで行われるある近似の操作で生まれるバイアスが最終推定結果に影響している可能性は拭えず、理論的に良いものかと思ってしまいました。
RでSLMモデル
SLMではspdepパッケージで実行できます。
また、用いたデータは国土地理院が提供する国土データのパッケージkokudosuuchiを利用して、引っ張ってきた茨城県のデータです。
データの整形部分はこちらのコードをみてください。
記述は、lm関数と同じようにできます。
> # SLM (spatial lag model)
> slm <- spreg(ln_price ~ station + tokyo, listw = W, dat, model = "lag")
> summary(slm)
Generalized stsls
Call:
spreg(formula = ln_price ~ station + tokyo, data = dat, listw = W,
model = "lag")
Residuals:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-1.653 -0.299 0.149 0.117 0.545 1.721
Coefficients:
Estimate Std. Error t-value Pr(>|t|)
(Intercept) 13.851248 1.842850 7.5162 5.639e-14 ***
station -83.075087 9.455732 -8.7857 < 2.2e-16 ***
tokyo -0.037486 0.195615 -0.1916 0.84803
lambda -0.317580 0.175377 -1.8108 0.07016 .
rho 0.748299 0.036774 20.3483 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
空間過程モデリング
例えば、効率よく鉱石を採掘したいと考えた場合、全てのポイントを採掘し鉱石の採掘するとコストがかかりすぎます。
いくつかのポイントのみ採掘を行い、その点の採掘量から未採掘点の採掘量が推定できれば嬉しいです。
このような問題を空間予測と呼ばれ、地球科学の分野でよく議論されています。
共分散関数とバリオグラム
推定に当たって、次にような期待値と分散・共分散はどの点において同じであるという弱定常性を仮定します。
E[y(s_i)]=\mu\\
Cov[y(s_i),y(s_j)]=\tau^2 c(d_{ij};r)
ここで、$d_{ij}$は点i,j間の距離であり、$r$は空間相関の減衰パターンを示すパラメータです。
$c(・)$は空間相関を表現する共分散関数であり、空間過程モデリングではこの関数をモデルリングことが主題になります。
共分散関数は、指数関数型、ガウス関数型、球型関数型などの種類があります。
- 指数関数型
c(d_{ij};r) = exp\left(-\frac{d_{ij}}{r}\right)
- ガウス関数型
c(d_{ij};r) = exp\left(-\frac{d_{ij}^2}{r^2}\right)
- 球型関数型
\begin{equation}
c(d_{ij};r)= \left \{
\begin{array}{l}
1-\frac{3d_{ij}}{2r} + \frac{d_{ij}^3}{2r^3}(if r \geq d_{ij} \geq 0) \\
0 (otherwise)
\end{array}
\right.
\end{equation}
- Matern型関数:指数型とガウス型を内包した関数
c(d_{ij};r,\nu) = \frac{2^{1-\mu}}{\Gamma(\nu)}exp\left(\sqrt{2 \nu }\frac{d_{ij}^2}{r^2}\right)^\nu K_{\nu}\left(\sqrt{2 \nu}\frac{d_{ij}}{r}\right)
実際のモデリングの際は、共分散関数を推定する際にはバイアスが乗る場合があります。
そのため、共分散関数と共役関係/データ間の非類似性をモデル化するものであるバリオグラムを推定する。
バリオグラムの定義は次のような式である。
\gamma (d_{ij};r) = c(0;r)-c(d_{ij};r)=E[\epsilon(s_i) - \epsilon (s_j)]^2
ここで、$\epsilon(s_i)$は回帰モデルの残差です。
実際の推定では、バリオグラム雲を作成し経験バリオグラムを推定します。
バリオグラム雲は$\gamma (d_{ij};r) =E[\epsilon(s_i) - \epsilon (s_j)]^2$を全ての観測地点ペア$(s_i,s_j)$についてをプロットしたものです。
経験バリオグラムはバリオグラム雲の値を$d_{ij}$の一定毎の平均値を求めることで推定します。
\gamma^* (d_{ij};r) = \frac{1}{2 \# N_r} \sum_{s_i \in N_r} E[\epsilon(s_i) - \epsilon (s_j)]^2
ここで、$N_r$はr番目の距離帯の中の標本ペアの集合、#$N_r$は$N_r$に含まれる標本の数です。
Krigingによる空間予測
Krigingは、観測点と予測点を同時に考えるモデルを設定し、予測の点の値を推定するものです。
モデルはトレンドと相関関数とノイズの重ね合わせであると考えます。
\begin{eqnarray}
\left[
\begin{array}{c}
y \\
y^* \\
\end{array}
\right]
=
\left[
\begin{array}{c}
X \\
x_*^` \\
\end{array}
\right] \beta
+
\left[
\begin{array}{c}
\epsilon \\
\epsilon_* \\
\end{array}
\right]
\end{eqnarray}
また、定常性と線型性の仮定をおきます。
- 定常性
E\left[
\begin{array}{c}
\epsilon \\
\epsilon_* \\
\end{array}
\right]=
\left[
\begin{array}{c}
0 \\
0 \\
\end{array}
\right],
Var\left[
\begin{array}{c}
\epsilon \\
\epsilon_* \\
\end{array}
\right]=
\left[
\begin{array}{cc}
\sigma^2I + \tau^2C_r& \tau^2c_{*r} \\
\tau^2c`_{*r}&\sigma^2I + \tau^2 \\
\end{array}
\right]
- 線型性
\hat y_* = \frac{\sum_j \omega_{*j} y_i}{\sum_j \omega_{*j}}
これらの式から、予測点の値を表現すると次にようになり、Kriging予測量と呼ばれています。
\hat y_* = x_*^`\hat \beta+\tau^2c`_{*r}(\sigma^2I + \tau^2C_r)^{-1}[y-X\hat \beta]
また、回帰係数$\hat \beta$は次を計算することにより推定することができます。
\hat \beta =[X`(\sigma^2I + \tau^2C_r)^{-1}X]^{-1}X`(\sigma^2I + \tau^2C_r)^{-1}y
活用方法
モデルにおける期待二乗誤差を最小化することは、期待される説明力を最大化することに相当しています。
期待二乗誤差が大きい場所は説明力が低く、十分なサンプルが存在していないと考えられます。
逆に期待二乗誤差小さい場所はサンプル数がより少なくても良い可能性があります。
これを利用して、観測点の最適化を考えることができます。
実際に都道府県の地下調査の評価地点を削減することが可能になっています。
観測点の配置を少しづつ変更しながら、目的関数による評価値が収束するまで繰り返し、最適な観測位置の推定を行います。
RでKrigingによる空間予測
kokudosuuchiパッケージで東大和,多摩,立川,日野のデータを読み込み、地下データのモデリングを行いたいと思います。
データの読み込み加工部分についてはこちらをみてください。
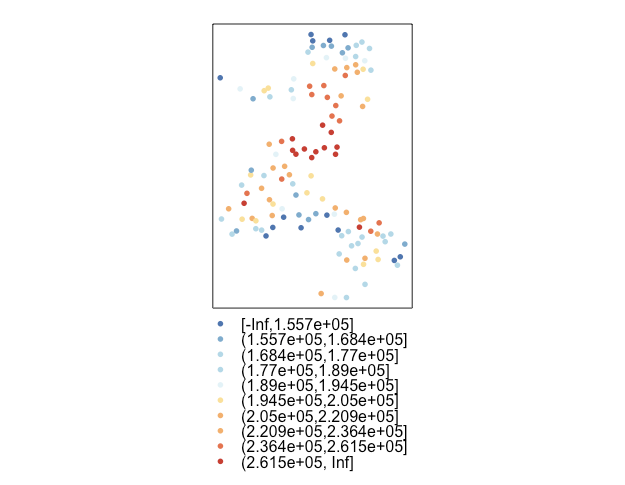
はじめに観測されている地価データを可視化してみます。
# 分布の確認
nc <- 8
cols <- rev(brewer.pal(n = nc, name = "RdYlBu"))
cuts <- c(-Inf, quantile(dat$price,probs=seq(0.1,0.9,0.1)), Inf)
spplot(dat, "price",cuts=cuts, col.regions = cols, col="transparent",cex=0.7) # 住宅地価をプロット
立川駅周辺は地価が比較的高そうです。また、南側の方はサンプリング間隔が広いようです
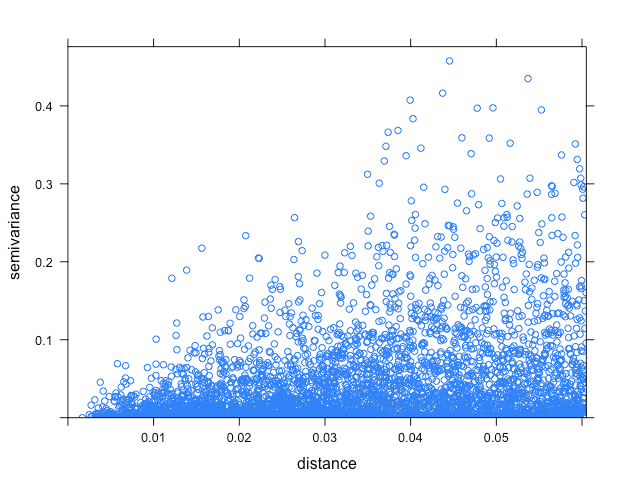
バリオグラムの推定を行います。はじめにバリオグラム雲を見てみます。
coordinates(mdat)=~px+py
# バリオグラム雲を生成
vario_cloud <- variogram(object = log(price) ~ tokyo + station,
data = dat,
cloud = T)
plot(vario_cloud)
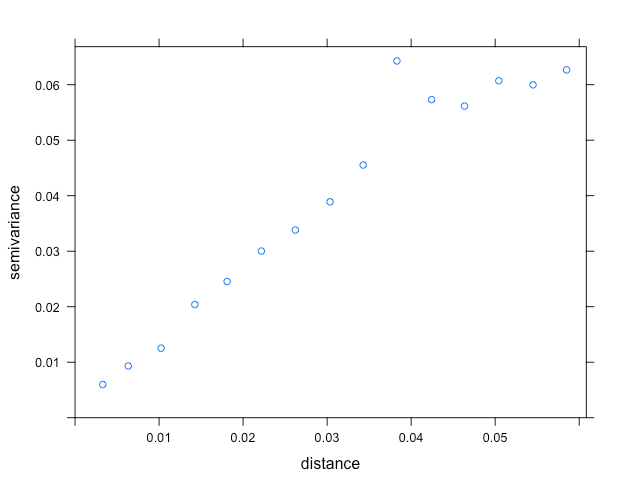
# 経験バリオグラムを求める
exp_vario <- variogram(object = log(price) ~ tokyo + station, data = dat)
plot(exp_vario)
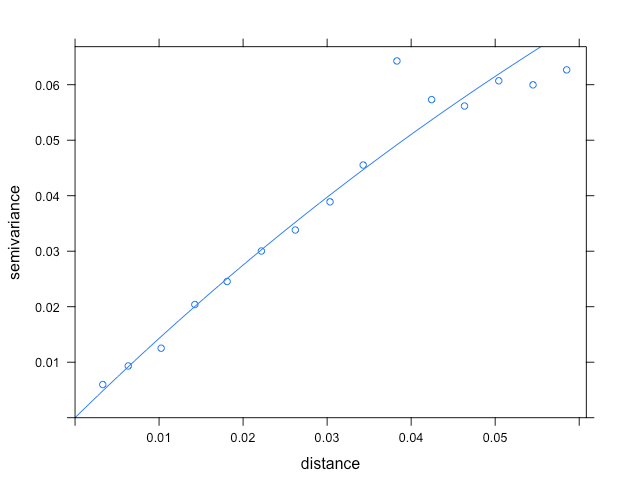
# 理論バリオグラムの推定(vgmでパラメータ推定の初期値を指定)
mvario <- fit.variogram(object = vario,
model = vgm(psill = 0.04,
model = "Exp",
range = 0.04,
nugget = 0.01))
plot(vario, mvario) #理論バリオグラム
特徴量+krigingによるモデリングと比較のための回帰モデルを作成しました。
# Regression kriging モデルを定義
stat_model <- gstat(formula= log(price) ~ tokyo + station,
data = dat,
model = mvario)
model_pred <- predict(stat_model, newdata = mdat)
mdat@data$predRK <- exp(model_pred$var1.pred) # 対数値を元に戻す
mdat@data$varRK <- model_pred$var1.var # 期待二乗誤差
# 比較用に普通の回帰モデル
l_model <- lm(log(price) ~ tokyo + station, data = dat@data) # 回帰
lm_pred <- exp(predict(l_model, newdata = mdat@data))
mdat@data$predLM <- lm_pred # 予測値
結果の可視化をしてみます。
nc <- 10
cols <- rev(brewer.pal(n = nc, name = "RdYlBu")) # 色分けを指定
rang <- range(mdat@data$predRK)
cuts <- seq(rang[1],rang[2], len = nc-1) # 色の区切り値を指定
# Regression krigingの予測値
spplot(mdat, "predRK",cuts=cuts, col.regions = cols, col="transparent",cex=1,pch=15)
# 回帰モデルの予測値
spplot(mdat, "predLM",cuts=cuts, col.regions = cols, col="transparent",cex=1,pch=15)
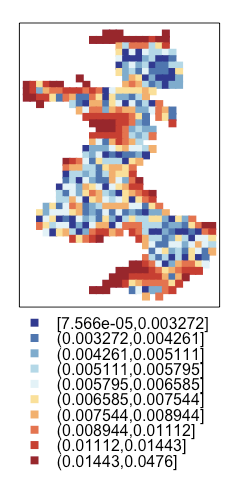
# Regression krigingの期待二乗誤差
rang <-range(mdat@data$varRK) # 予測値の最小値・最大値
cuts<-quantile(mdat@data$varRK,probs=seq(0,1,0.1)) # 色の区切り値を指定
spplot(mdat, "varRK",cuts=cuts, col.regions = cols, col="transparent",cex=1,pch=15)
左から回帰krigingモデルの予測、回帰モデルの予測、回帰krigingモデルの予測の二乗誤差です。
普通の回帰モデルだと地理的な要因は加味されず全体的に同程度の値になっています。
krigingモデルだと、立川駅周辺の地価が高いことが表現できています。
また、サンプリング間隔が広かった南の方の地域は誤差が大きいようです。
時空間データモデリング
空間モデリングに時間発展を考えることで、より柔軟に現象を表現できるようになります。
空間モデリングには静的モデリングと動的モデリングの二種類があります。
- 静的モデリング
- 3次元空間上で共分散関数を推定
- 計算効率が悪く、時間発展がとらえずらい
- 動的モデリング
- 状態空間モデル:時間発展を捉える
- 地球統計モデル:空間発展を捉える
空間データの状態空間モデル
状態空間モデルは、時系列相関のある状態変数の時間発展を表現するProcess Modelと、状態変数から観測値を得るData Modelからなります。
空間データの状態空間モデルでは、Process Modelに空間相関を加味するようになります。
なお、空間相関$\omega_t$は時間発展はせずに独立となります。
y_t = X_t\beta + z_t + \epsilon_t \epsilon_t \sim N(0,\sigma^2 I) \\
z_t = \lambda z_{t-1} + \omega_t \omega_t \sim N(0,\tau^2 C_r)
グラフで表現すると次のようになります。

Rで空間データの状態空間モデル
<気が向いたらあげます>
終わりに
講座では、他にも理論部分や基本的な統計モデルの考え方、高速化手法、様々なモデルの拡張について触れていました。
今まで関わりがなかった分野でしたので、面白かったです。
仕事で使うかは未知数ですが、何かしらのデータに適用していきたいものです。
個人的には、各パッケージがtidyに扱えないので、少し扱いづらい気がしました。
いい感じに扱えるパッケージがあるんですかね。