はじめに
高橋・渡辺著の「欠測データ処理 Rによる単一代入法と多重代入法」を読んで欠測データ処理の基礎を勉強しましたのでまとめます。
特に多重代入法による処理方法が気になっていたので、中心にまとめていきます。
欠測データについて
欠測の種類
- MCAR(Missing Completely At Random:完全にランダムな欠損
- MAR(Missing At Random):観測データに依存する欠損
- MNAR(Missing Not At Random):欠損データに依存する欠損
欠測の代入法方
欠測の代入方法は単一代入法と多重代入法の二つがある。
単一代入法
得られているデータから欠損している箇所の値を一意に求め、代入する方法。
確定的代入法
-
平均値代入法
欠測を欠測していない値の平均値で補完する方法。
この方法は百害あって一利なしとされている。 -
確定的回帰代入法
欠測がある変数を目的変数、欠測がない変数を目的変数をして回帰モデルを作成し、欠測値を予測することで補完する方法。
ガウス・マルコフの仮定とMARの仮定の両方が満たされた場合、回帰モデルのパラメータは最良線形不偏推定量である。
この仮定が満たされていれば、ロジスティック回帰や二乗項をいれたモデルを用いても良い。 -
比率代入法
切片のない単回帰分析の構造をしたモデルを用いてで代入値を予測する方法。
また、説明変数の値が大きくなると目的変数のばらつきが増加することが往々にある。
そのため、モデルの誤差の分散$\epsilon_i$は、$N(0,\sigma^2X_i^{2\theta})$に従う。 -
ホットデック法
欠測していないデータが似通っている対象の値を用いて欠測値を代入する方法。
数量項目でも質的項目でも利用することができる。
データの近さは、ユーグリット距離をはじめとする様々な距離定義を用いて算出する。
確率的代入法
- 確率的回帰代入法
確定的回帰代入法では、不偏推定を行うことができるが、データのばらつきの表現が著しく損なわれている状態である。
この点を解消するため確定的回帰代入法における、回帰モデルに誤差項を追加したモデルで予測した値で欠測値を補完する方法。
多重代入法
多重代入法は、欠測データの分布から独立かつ無作為に抽出されたM個のシミュレーション値によって欠測値を置き換えるものである。
この代入法の目的は個々の値を完全に復元させることではなく、母集団のパラメータの推定です。
MARであると仮定して、観測データを条件とする欠測データの事後予測確率を構築する。
多重代入法による分析の流れ
N個の代入済みのデータを生成し、それぞれのデータでモデル作成や分析を行う
その後にその結果を統合する。
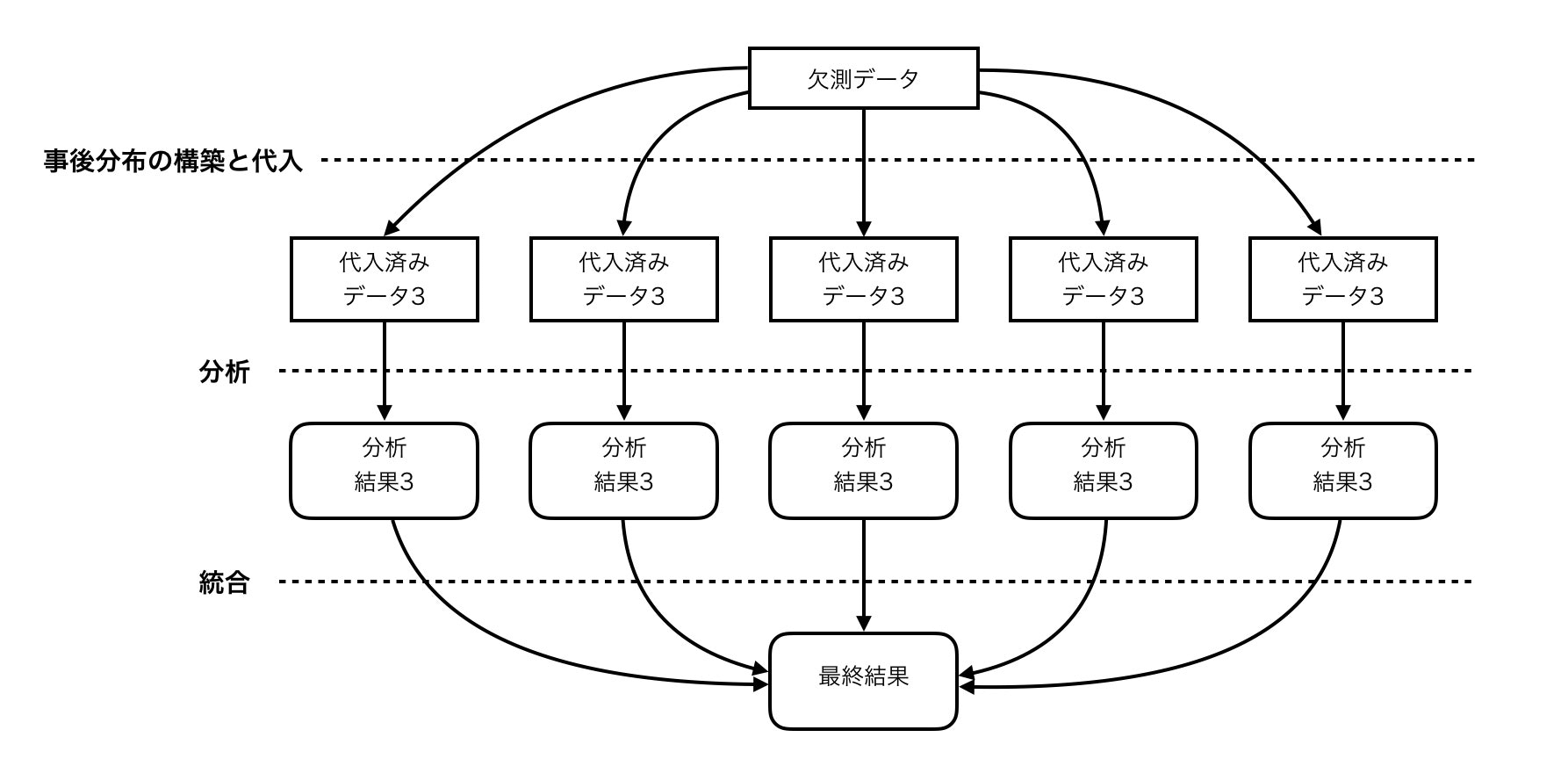
統合方法は、次のように行なっていく。
統合されたパラメータ$\theta_M$は、$m$番目の代入済みデータセット推定されたパラメータ$\hat \theta_m$を算術平均で求める。
\theta_M = \frac{1}{M}\sum_{m=1}^{M} \hat \theta_m
多重代入法におけるパラメータの分散は2種類存在し、代入内分散と代入間分散である。
代入内分散は、パラメータ$\hat \theta_m$の分散$var(\hat \theta_m)$の算術平均である。
\hat W_M = \frac{1}{M} \sum_{m=1}^{M} var(\hat \theta_m)
代入間分散は、$\hat \theta_m$に自由度が1つ減っているため次にように求める。
\hat B_M = \frac{1}{M-1} \sum_{m=1}^{M} (\hat \theta_m - \hat \theta_m)^2
また、$\hat \theta_m$の分散$T_M$は代入内分散と代入間分散と合算して求める。
T_M=\hat W_M + (1+\frac{1}{M})\hat B_M
RのサンプルデータであるUSJudgeRatingsデータの一部を欠測させることでサンプル欠測データを作成した。
また、VIMパッケージを利用してデータの欠測状態を確認した。
set.seed(8792)
data(USJudgeRatings)
summary(USJudgeRatings)<img width="893" alt="多重代入法の説明.jpg" src="https://qiita-image-store.s3.amazonaws.com/0/197919/8c70bd0b-55f6-adfd-bbdf-06609d1ea96e.jpeg">
data.mis <- missForest::prodNA(USJudgeRatings[,c(2:6)], noNA = 0.2) %>% cbind(USJudgeRatings[,-c(2:6)])
library(VIM)
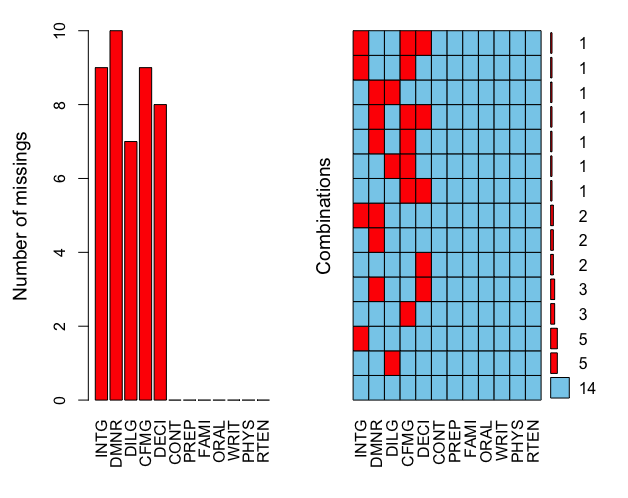
aggr(data.mis, prop=FALSE, number=TRUE)
左は各変数の欠測場所の数、右は欠測位置の状態である。
多重代入法
多重代入法のアルゴリズムとRでの実行
多重代入法のアルゴリズムは主に3つあります。
DAアルゴリズム
DAアルゴリズムはMCMC用い、前期までの値を条件としてパラメータ推定値を繰り返し置き換え更新していく方法。
観測値$Y_{obs}$と繰り返し時点$t$におけるパラメータ$\theta^{(t)}$を条件として、欠測値の代入値$Y_{mis}^{(t+1)}$を生成する。
そして、観測値と代入値から、次のステップのパラメータ$\theta^{(t)}$を生成する
この2つのステップを収束するまでT回繰り返し、最終的な代入値を取得する
Y_{mis}^{(t+1)} \sim Pr(Y_{mis} \mid Y_{obs}, \theta^{(t)}) \\
\theta^{(t)} \sim Pr(\theta \mid Y_{obs}, Y_{mis}^{(t+1)})
Rでの実装はnorm2が紹介されていたが、CRAN等から消えているようです。
FCSアルゴリズム
完全条件付き指定(FCS:fully conditional specification)はDAアルゴリズムの代替手段として提案されたアルゴリズム。
欠測値を補完したい変数$Y_j$の観測値$Y_{j,obs}$とそれ以外の変数$\hat Y_{-j}$を条件として代入モデルで未知パラメータ$\hat \theta_j^{(t)}$を推定する。
推定した未知パラメータも条件付けとした、代入モデルによりstep t における欠測値の代入値$\hat Y_j^{(t)}$を推定する。
\hat \theta_j^{(t)} \sim Pr(\theta_j^{(t)} \mid Y_{j,obs},\hat Y_{-j}^{(t)})\\
\hat Y_j^{(t)} \sim Pr(Y_{j,mis} \mid Y_{j,obs},\hat Y_{-j}^{(t)},\hat \theta_j^{(t)})
この未知パラメータと代入値の推定を収束するまで繰り返す。
この時、収束とは分布が安定したことを意味する。
このようにFCSはギプスサンプラーでMCMCの一種である。
Rではmiceパッケージで提供されている。
imp <- mice(data.mis, m = 10, maxit = 50, method = "norm", printFlag = FALSE, seed = 12345)
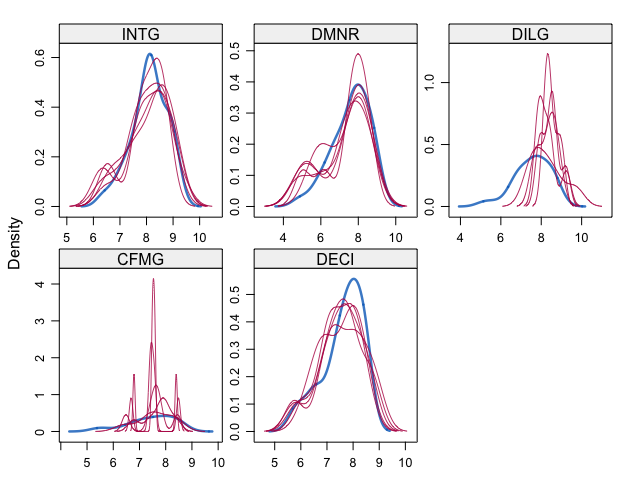
densityplot(imp)
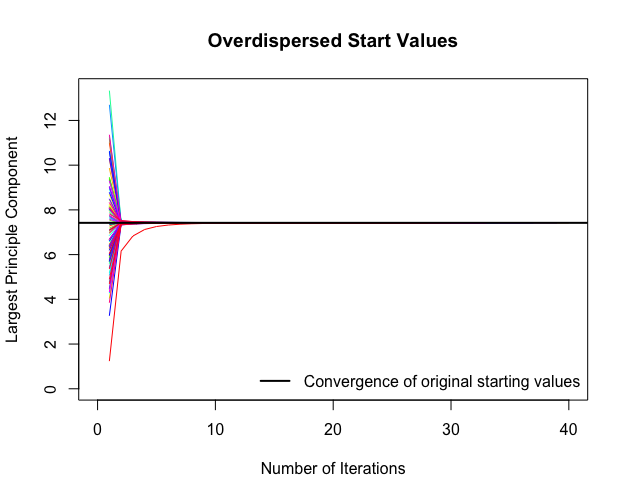
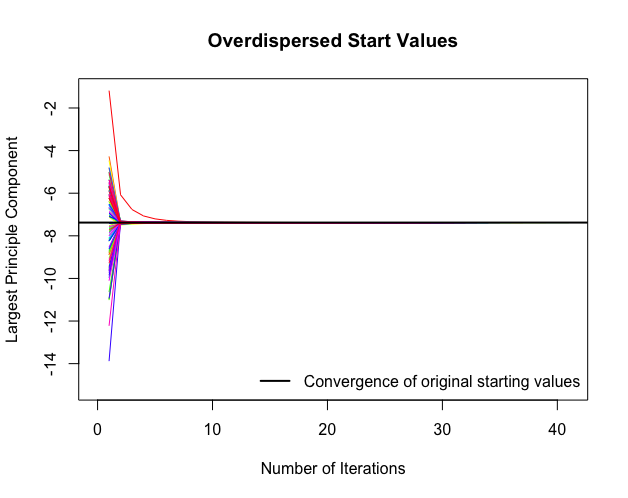
disperse(data.out, dims = 1, m =100)
観測値と体入地の密度の比較を行う。
赤線が代入値、青線が観測値をあらわしている。
NARの場合では、代入値と観測値の分布がずれていることが期待される。
今回はNARの仮定を満たしていない可能性が高く両者の分布は一致する傾向にある。
どのような値が代入されているかを確認してみましょう。
> #補完データを確認してみる
> complete(imp,1)[,c(1:5)] %>% head
INTG DMNR DILG CFMG DECI
1 7.900000 7.700000 7.300000 7.10000 7.400000
2 8.900000 8.251108 8.611697 7.80000 8.100000
3 8.503248 7.800000 7.800000 7.36411 7.600000
4 8.800000 8.500000 8.221343 8.30000 8.500000
5 6.400000 5.144525 6.500000 6.00000 6.200000
6 8.800000 8.700000 8.500000 7.90000 7.998068
> data.mis[,c(1:5)] %>% head # NAの場所を確認
INTG DMNR DILG CFMG DECI
AARONSON,L.H. 7.9 7.7 7.3 7.1 7.4
ALEXANDER,J.M. 8.9 NA NA 7.8 8.1
ARMENTANO,A.J. NA 7.8 7.8 NA 7.6
BERDON,R.I. 8.8 8.5 NA 8.3 8.5
BRACKEN,J.J. 6.4 NA 6.5 6.0 6.2
BURNS,E.B. 8.8 8.7 8.5 7.9 NA
> USJudgeRatings[,c(1:5)] %>% head #実際の値を確認
CONT INTG DMNR DILG CFMG
AARONSON,L.H. 5.7 7.9 7.7 7.3 7.1
ALEXANDER,J.M. 6.8 8.9 8.8 8.5 7.8
ARMENTANO,A.J. 7.2 8.1 7.8 7.8 7.5
BERDON,R.I. 6.8 8.8 8.5 8.8 8.3
BRACKEN,J.J. 7.3 6.4 4.3 6.5 6.0
BURNS,E.B. 6.2 8.8 8.7 8.5 7.9
EMBアルゴリズム
EMBアルゴリズムはExpectation-Maximization with Bootstrappingの略であり、EMアルゴリズムとノンパラメトリック・ブートストラップから構成されるアルゴリズム。
まず、ブートストラップ法による再標本をM個得る。
その標本に対し、EMアルゴリズム利用して、欠測値を補完していく。
Eステップで欠損値を含む不完全データ$Y$とt回目のパラメータ推定値$\theta^{(t)}$を条件とした、完全データの対数尤度の条件付き期待値($Q$関数)を計算する。
Q(\theta \mid \theta^{(t)}) = \int l(\theta \mid Y)Pr(Y_{mis} \mid Y_{obs},\theta^{(t)})dY_{mis}
Mステップにおいて、Q関数を最大にするt+1 ステップにおけるパラメータを次のように推定する。
\theta^{(t+1)}=argmax_{\theta} Q(\theta \mid \theta^{(t)})
このステップを値が収束するまで繰り返す。
この時の、収束はパラメータがある一点に収束したことを意味する。
また、EMアルゴリズムの特性でもある、大域的最適解と局所的最適解が一致しない場合が存在するため、複数の初期値からアルゴリズムの施行を行う必要がある。
library(Amelia)
set.seed(8792)
M <- 5 #リサンプリングの数
data.out <- amelia(data.mis, m=M)
overimpute(data.out,var = 6)
data.mids <- datlist2mids(data.out$imputations)
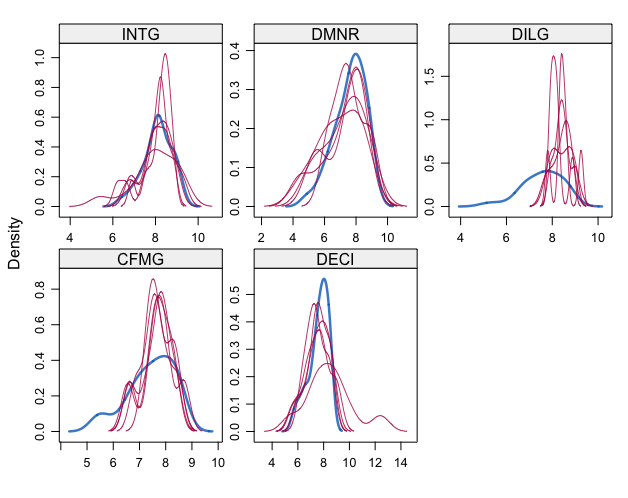
densityplot(data.mids)
disperse(data.out, dims = 1, m =100)
完全データと比較する
> complete(imp,1)[,c(1:5)] %>% head
INTG DMNR DILG CFMG DECI
1 7.900000 7.700000 7.300000 7.10000 7.400000
2 8.900000 8.251108 8.611697 7.80000 8.100000
3 8.503248 7.800000 7.800000 7.36411 7.600000
4 8.800000 8.500000 8.221343 8.30000 8.500000
5 6.400000 5.144525 6.500000 6.00000 6.200000
6 8.800000 8.700000 8.500000 7.90000 7.998068
> data.mis[,c(1:5)] %>% head # NAの場所を確認
INTG DMNR DILG CFMG DECI
AARONSON,L.H. 7.9 7.7 7.3 7.1 7.4
ALEXANDER,J.M. 8.9 NA NA 7.8 8.1
ARMENTANO,A.J. NA 7.8 7.8 NA 7.6
BERDON,R.I. 8.8 8.5 NA 8.3 8.5
BRACKEN,J.J. 6.4 NA 6.5 6.0 6.2
BURNS,E.B. 8.8 8.7 8.5 7.9 NA
> USJudgeRatings[,c(1:5)] %>% head #実際の値を確認
CONT INTG DMNR DILG CFMG
AARONSON,L.H. 5.7 7.9 7.7 7.3 7.1
ALEXANDER,J.M. 6.8 8.9 8.8 8.5 7.8
ARMENTANO,A.J. 7.2 8.1 7.8 7.8 7.5
BERDON,R.I. 6.8 8.8 8.5 8.8 8.3
BRACKEN,J.J. 7.3 6.4 4.3 6.5 6.0
BURNS,E.B. 6.2 8.8 8.7 8.5 7.9
t検定における多重代入法
不完全データにおける平均値の検定では次のt値を用いる。
ここで$t_{\nu}$は自由度$\nu$のt分布に従う。
t_{\nu}=\frac{\hat \theta_M-\theta_0}{\sqrt{T_M}}\\
AmeliaとMKmiscにる一標本t検定
USJudgeRatingsデータのINTG()が平均が7.8であるかどうかを検定します。
帰無仮説を$\mu=7.8$, 対立仮説を$\mu \neq 7.8$、棄却域は$\alpha=0.05$として検定を実施する。
とりあえず、完全データの場合の検定を行います。
> # 普通の一標本t検定
> t.test(USJudgeRatings$INTG, mu = 7.8)
One Sample t-test
data: USJudgeRatings$INTG
t = 1.8811, df = 42, p-value = 0.0669
alternative hypothesis: true mean is not equal to 7.8
95 percent confidence interval:
7.783915 8.257946
sample estimates:
mean of x
8.02093
帰無仮説は棄却できず、平均は7.8ではないと言えない。
次にMKmiscパッケージを利用して多重代入法による検定を行いました。
> library(MKmisc)
>
> M <- 5
> set.seed(1234)
> a.out <- amelia(data.mis, m=M)
略
> mi.t.test(a.out$imputation, x="INTG", mu = 7.8)
Multiple Imputation One Sample t-test
data: Variable INTG
t = 2.6544, df = 35.061, p-value = 0.01187
alternative hypothesis: true mean is not equal to 7.8
95 percent confidence interval:
7.871355 8.335342
sample estimates:
mean SD
8.1033489 0.7494073
帰無仮説は棄却され、平均は7.8ではないと言える。
重回帰分析における多重代入法
欠測値に対して単一代入法を行なった場合、推定されたパラメータの推定値は偏りが発生してしまう。
欠損値があるデータに対する重回帰分析においても多重代入法を適用することで、偏りを軽減したパラメータを推定することができる。
Ameliaパッケージで多重代入法による重回帰分析
data.midsにおけるCONTを目的変数に重回帰分析を行う。
リサンプリング数は5とした。
> # とりあえずの重回帰分析
> model.true <- lm(CONT ~ ., data=USJudgeRatings)
> summary(model.true)
Call:
lm(formula = CONT ~ ., data = USJudgeRatings)
Residuals:
Min 1Q Median 3Q Max
-1.5785 -0.4458 0.0438 0.3449 2.6167
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.61673 4.29050 1.542 0.1332
INTG 0.86349 0.99092 0.871 0.3902
DMNR -1.19565 0.60266 -1.984 0.0562 .
DILG -1.74425 0.94208 -1.851 0.0736 .
CFMG 2.17518 0.97503 2.231 0.0331 *
DECI -0.09398 1.01672 -0.092 0.9269
PREP 1.56003 1.63625 0.953 0.3478
FAMI -0.96150 1.84811 -0.520 0.6066
ORAL 2.24665 1.99440 1.126 0.2686
WRIT -2.68150 2.12548 -1.262 0.2165
PHYS -0.62336 0.53262 -1.170 0.2508
RTEN 0.61219 1.23741 0.495 0.6243
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8122 on 31 degrees of freedom
Multiple R-squared: 0.45, Adjusted R-squared: 0.2549
F-statistic: 2.306 on 11 and 31 DF, p-value: 0.03327
次に多重代入法による重回帰分析を行います。
> model.am <- lm.mids(CONT ~ ., data=data.mids)
> summary(pool(model.am)) #各パラメータ確認
estimate std.error statistic df p.value
(Intercept) -9.4485362 20.4831482 -0.4612834 1.3762969 0.6501124
INTG 5.1659261 6.6032453 0.7823314 1.0345839 0.4441753
DMNR -3.3425262 4.2305949 -0.7900842 0.8926102 0.4397485
DILG -3.6013973 4.8831185 -0.7375200 1.1225404 0.4702979
CFMG 2.4544544 1.4397039 1.7048328 4.5323082 0.1053984
DECI 2.3341316 4.4423376 0.5254287 1.0594546 0.6056884
PREP 4.4937065 6.8531852 0.6557107 1.4530301 0.5202918
FAMI -4.9387435 8.2683785 -0.5973050 1.1639435 0.5577325
ORAL 2.0219426 2.7094598 0.7462530 8.7407748 0.4651358
WRIT -2.9341027 2.2015825 -1.3327244 18.0272036 0.1992231
PHYS -0.2264913 0.7899002 -0.2867341 5.5846333 0.7775854
RTEN 0.5579775 2.6813711 0.2080941 2.8063293 0.8374884
> pool.r.squared(model.am) #決定係数の推定値
est lo 95 hi 95 fmi
R^2 0.5671216 0.09424856 0.8609327 NaN
決定係数が高く見積もられているようです。
ざっくりと以上です。