Rで行う基本的な統計検定とその選択フローチャート4
このシリーズでは生物学で用いられている基本的な統計検定をRで行う際の手順と実際のコードを特集します。自身のデータセットの特徴と実験目的から適切な統計検定法を選択し、それをRで実行できるようになるための指針となれば幸いです。
第一回:平均値の差の検定(2群)
第二回:一元配置の分散分析
第三回:一元配置の多重比較
第四回:二元配置の分散分析
第五回:比率の差の検定
第六回:サンプルサイズの設計法
第七回:回帰分析
第四回 二元配置の分散分析
4.1 パラメトリック検定法のRソースコード
パラメトリック検定のソースコードを紹介します。分散分析から多重比較までの各検定法を紹介します。
4.1.1 各水準の繰り返し数が全ての1の場合のtwo-way ANOVA
4.1.2 各水準の繰り返し数が等しい、または周辺度数に比例する場合のtwo-way ANOVA
4.1.3 各水準の繰り返し数が異なり、周辺度数にも比例しない場合のtwo-way ANOVA
4.2 二元配置分散分析のノンパラメトリック版にあたる分析法
4.1 多重比較の検定手法をRで実行してみる(パラメトリック)
参照:https://toukeier.hatenablog.com/entry/two-way-anova-in-r
https://www1.doshisha.ac.jp/~mjin/R/Chap_13/13.html
母集団が正規分布に従う&各群が等分散と仮定できる場合、パラメトリックな検定手法を使って、多群の中で平均値に差があるか(二元配置分散分析)、どの群に差があるか(多重比較)を検定することになります。
母集団が正規分布に従う&各群が等分散と仮定できる場合、各群の平均値に差があるかを調べることができる。またデータに対応があるか(反復測定かどうか)を確認し、対応なしの場合は通常のtwo-way ANOVAを適用する。
対応ありの場合は、水準が2の場合はRepeated measures two-way ANOVAを、水準が3以上ではMauchly’s sphericity testを行なって球面性を確認してRepeated measures two-way ANOVAを適用する。球面性が確認できない場合は、自由度を補正してANOVAを行う必要がある。ここでは対応なしのtwo-way ANOVAのみを取り扱う。
またANOVAではどの群とどの群に差があるかは言及できない。群間の差を検出するためには、多重比較法を用いる必要がある。F統計量を用いる多重比較法(Scheffe, Games/Howell, Fisher's PLSD)を使う場合は、事前にANOVAを行なって有意差があることを確認しておく必要があるが、F統計量を用いない多重比較法(Dunnet, Tukey-Kramer, Bonferroni)を使う場合は必ずしも事前のANOVAは必要でない。
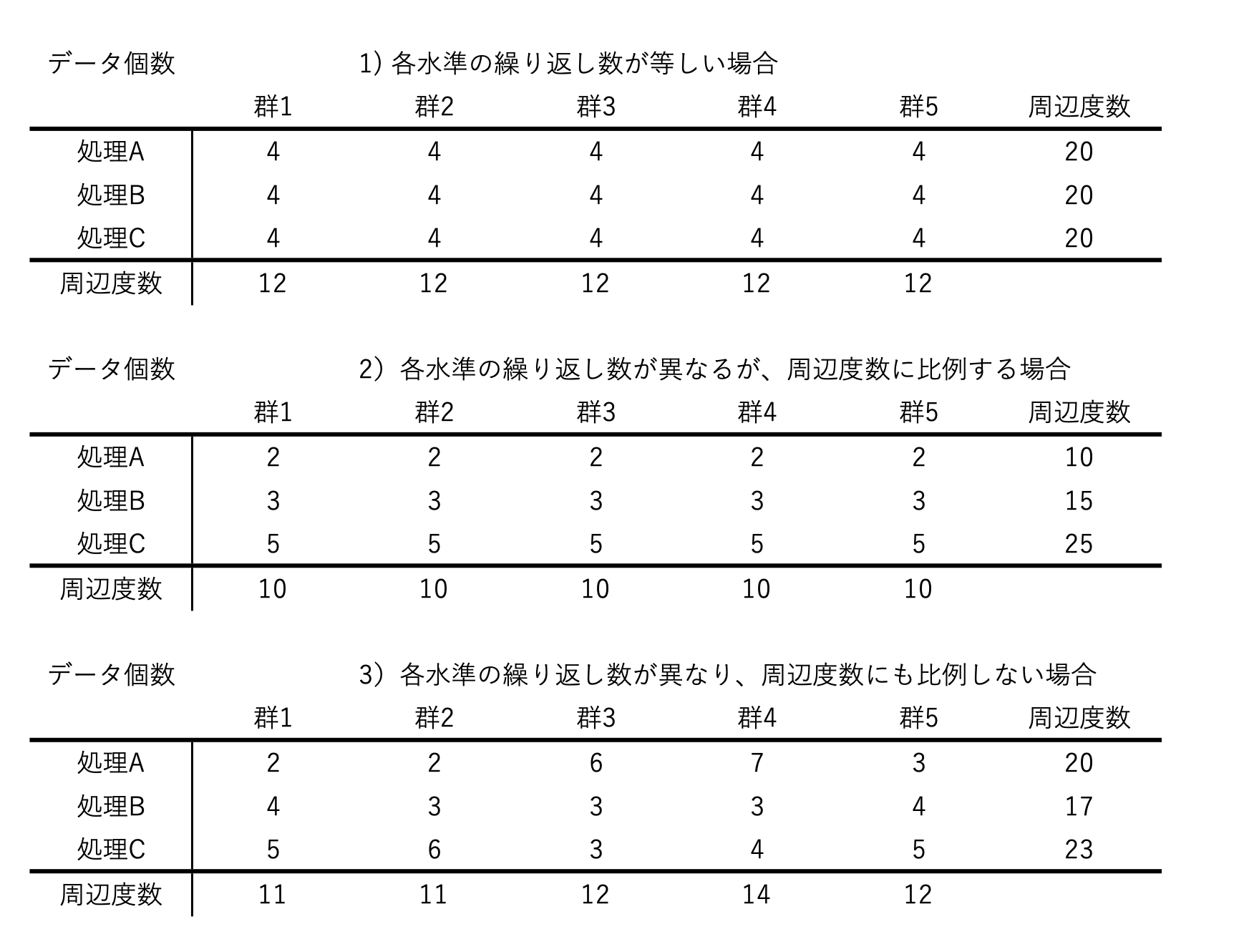
まず二元配置分散分析では、各水準におけるデータ数によって以下の3つに大別される。
1)各水準の繰り返し数が全ての1の場合
2)各水準の繰り返し数(データ数)が等しい場合
3)各水準の繰り返し数が異なるが、周辺度数に比例する場合
4)各水準の繰り返し数が異なり、周辺度数にも比例しない場合
4.1.1 各水準の繰り返し数が全ての1の場合のtwo-way ANOVA
ではまずは、1)に適用できる手法をやってみる!
データセットは『統計ソフトRによる多次元データ処理入門(日新出版)103p』より拝借する。
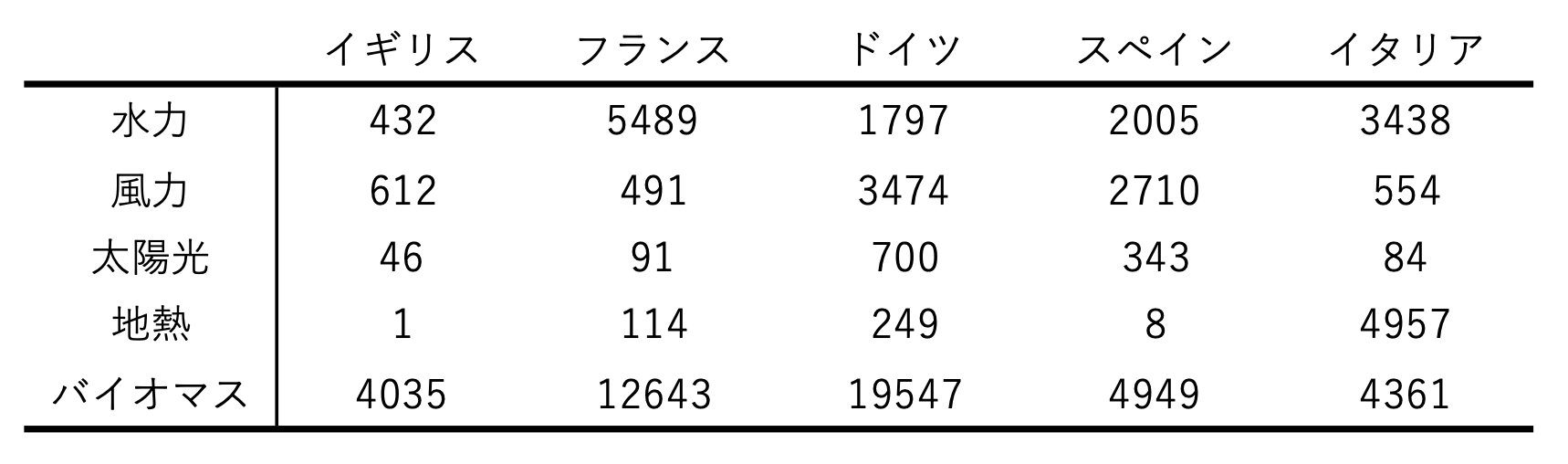
国と発電方法の二元配置分散分析を行ってみる
帰無仮説は
Ha0:発電方法の種類について各水準の平均値は等しい
Hb0:国について各水準の平均値は等しい
x<-c(432,612,46,1,4035,5489,491,91,114,12643,1797,3474,700,249,19547,2005,2710,343,8,4949,3438,554,84,4957,4361)
a <- rep(1:5, each=5)
b <- rep(1:5, 5)
data.frame(x, a, b) #データ構造を確認
twoway.anova(x, a, b)
df <- data.frame(f1=as.factor(a), f2=as.factor(b),x=x)
summary(aov(x ~ f1+f2, df))
結果
SS d.f. MS F value P value
a 50961566 4 12740391 1.144379 0.371365529
b 253705197 4 63426299 5.697133 0.004777625
e 178128319 16 11133020 NA NA
T 482795082 24 20116462 NA NA
Df Sum Sq Mean Sq F value Pr(>F)
f1 4 50961566 12740391 1.144 0.37137
f2 4 253705197 63426299 5.697 0.00478 **
Residuals 16 178128319 11133020
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
というわけで、国についての各水準での差は認められないものの、発電方法については各水準間で平均値に差があると言える。
4.1.2 各水準の繰り返し数が等しい、または周辺度数に比例する場合のtwo-way ANOVA
次に2)および3)の場合に適用できる手法を行ってみる。
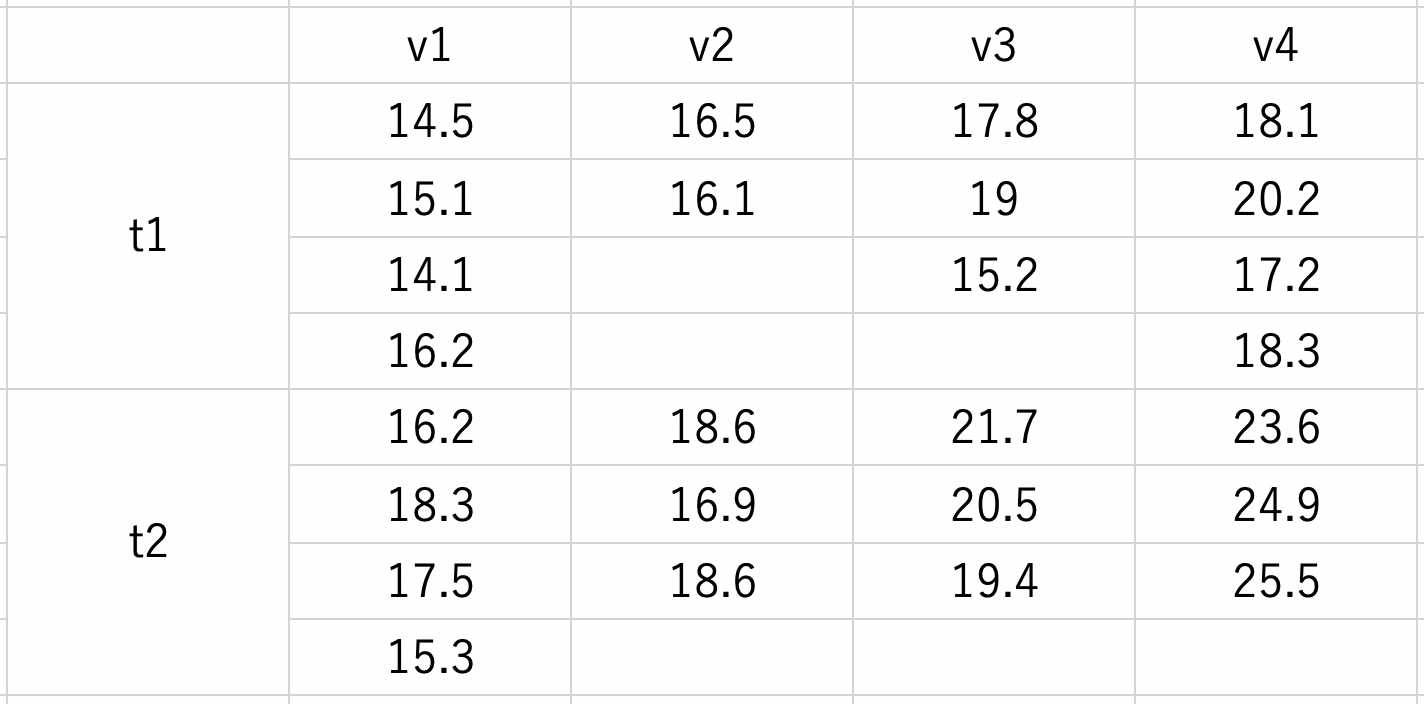
エレクトロポレーション法での細胞トランスフェクションの条件検討をするために、パルス時間と電圧の2因子でトランスフェクション効率を調べた。このデータセットを用いてtwo-way ANOVAをRで実行してみる。帰無仮説は
Ha0:パルス時間について、各水準間で平均値に差はない
Hb0:電圧について、各水準間で平均値に差はない
He0:交互作用はない
t1 <- c(14.5, 15.1, 14.1, 16.5, 16.1, 15, 17.8, 19, 15.2, 18.1, 20.2, 17.2)
t2 <-c(16.2, 15.3, 17.5, 18.6, 16.9, 18.6, 21.7, 20.5, 19.4, 23.6, 24.9, 25.5)
dat<-data.frame(A=factor(c(rep("t1",12),rep("t2",12))),B=factor(rep(c(rep("v1",3), rep("v2",3), rep("v3",3),rep("v4",3)),2)),y= c(t1,t2))
#Aに因子t(パルス時間)を、Bに因子v(電圧)を、yにスコアを格納する
summary(aov(y~A*B,data=dat)) #交互作用をみない時は*を+に変える
結果
Df Sum Sq Mean Sq F value Pr(>F)
A 1 66.33 66.33 46.333 4.21e-06 ***
B 3 126.64 42.21 29.485 9.40e-07 ***
A:B 3 17.79 5.93 4.142 0.0237 *
Residuals 16 22.91 1.43
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
以上からパルス時間、電圧、および両者の交互作用について帰無仮説は棄却され、パルス時間、電圧の両方で群間に差があり、交互作用も存在すると考えられる。
またはhttp://aoki2.si.gunma-u.ac.jp/R/twoway-anova.htmlに従った手法では、
x <- c(14.5, 15.1, 14.1, 16.5, 16.1, 15, 17.8, 19, 15.2, 18.1, 20.2, 17.2, 16.2, 15.3, 17.5, 18.6, 16.9, 18.6, 21.7, 20.5, 19.4, 23.6, 24.9, 25.5)
a <- rep(rep(1:4, each=3), 2)
b <- rep(1:2, each=12)
data.frame(x, a, b) #データフレームの確認
twoway.anova(x, a, b)
df <- data.frame(f1=as.factor(a), f2=as.factor(b),x=x)
summary(aov(x ~ f1+f2+f1:f2, df))
結果
$Model1
SS d.f. MS F value P value
a 126.63792 3 42.212639 29.484963 9.403252e-07
b 66.33375 1 66.333750 46.333236 4.214152e-06
a*b 17.79125 3 5.930417 4.142317 2.373442e-02
e 22.90667 16 1.431667 NA NA
T 233.66958 23 10.159547 NA NA
$Model2
SS d.f. MS F value P value
a 126.63792 3 42.212639 7.117989 0.07062156
b 66.33375 1 66.333750 11.185344 0.04424086
a*b 17.79125 3 5.930417 4.142317 0.02373442
e 22.90667 16 1.431667 NA NA
T 233.66958 23 10.159547 NA NA
Df Sum Sq Mean Sq F value Pr(>F)
f1 3 126.64 42.21 29.485 9.40e-07 ***
f2 1 66.33 66.33 46.333 4.21e-06 ***
f1:f2 3 17.79 5.93 4.142 0.0237 *
Residuals 16 22.91 1.43
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
以上からf1(変数a = 電圧)、f2(変数b = パルス時間)およびこれらの交互作用について帰無仮説を棄却し、水準間でトランスフェクション効率が異なり、交互作用も認められることと言える。
4.1.3 各水準の繰り返し数が異なり、周辺度数にも比例しない場合のtwo-way ANOVA
最後に、4)のように各水準でサンプル数がバラバラである場合を考えてみる。
x <- c(14.5, 15.1, 14.1, 16.2, 16.5, 16.1, 17.8, 19, 15.2, 18.1, 20.2, 17.2, 18.3, 16.2, 18.3, 17.5, 15.3, 18.6, 16.9, 18.6, 21.7, 20.5, 19.4, 23.6, 24.9, 25.5)
a <- c(rep(1,13),rep(2,13))
b <- c(1,1,1,1,2,2,3,3,3,4,4,4,4,1,1,1,1,2,2,2,3,3,3,4,4,4)
data.frame(x, a, b) #データフレームの確認
twoway.anova(x, a, b)
library(car)
df <- data.frame(f1=as.factor(a), f2=as.factor(b),x=x)
Anova(aov(x ~ f1+f1 * f2, df))
結果
SS d.f. MS F value P value
a 70.31434 1 70.314335 47.382219 1.943517e-06
b 121.23735 3 40.412451 27.232450 6.573594e-07
a*b 21.74790 3 7.249301 4.885035 1.173805e-02
e 26.71167 18 1.483981 NA NA
T 227.30038 25 9.092015 NA NA
Anova Table (Type II tests)
Response: x
Sum Sq Df F value Pr(>F)
f1 70.314 1 47.382 1.944e-06 ***
f2 121.237 3 27.232 6.574e-07 ***
f1:f2 21.748 3 4.885 0.01174 *
Residuals 26.712 18
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
以上からf1(変数a = 電圧)、f2(変数b = パルス時間)およびこれらの交互作用について帰無仮説を棄却し、水準間でトランスフェクション効率が異なり、交互作用も認められることと言える。
4.2 二元配置分散分析のノンパラメトリック版にあたる分析法
二元配置の分散分析は各水準が正規分布に従っていることを仮定している。そのため正規性が確認できないデータセットには適用しにくい。そこで、二元配置のデータセットのノンパラメトリックな分析手法として整列ランク変換(Aligned Rank Transform:ART)という手法を用いて分散分析を行う。
参照:https://hikaru1122.hatenadiary.jp/entry/2017/05/20/195301
http://depts.washington.edu/acelab/proj/art/index.html
https://cran.r-project.org/web/packages/ARTool/readme/README.html
さっそくやってみよう。データセットは先ほどの4.1.3のデータセットを使う。
install.packages("ARTool") #JapanのミラーサイトではインストールできなかったのでUS[MI]を選択した
library(ARTool)
x <- c(14.5, 15.1, 14.1, 16.2, 16.5, 16.1, 17.8, 19, 15.2, 18.1, 20.2, 17.2, 18.3, 16.2, 18.3, 17.5, 15.3, 18.6, 16.9, 18.6, 21.7, 20.5, 19.4, 23.6, 24.9, 25.5)
a <- c(rep(1,13),rep(2,13))
b <- c(1,1,1,1,2,2,3,3,3,4,4,4,4,1,1,1,1,2,2,2,3,3,3,4,4,4)
f1=as.factor(a)
f2=as.factor(b)
df <- data.frame(f1, f2,x=x)
henkan = art(x ~ f1*f2, data=df) #art関数を使ってデータを整列ランクに変換する
summary(henkan)
整数ランク変換の結果(全ての出力結果が0になってることが望ましいらしい)
Aligned Rank Transform of Factorial Model
Call:
art(formula = x ~ f1 * f2, data = df)
Column sums of aligned responses (should all be ~0):
f1 f2 f1:f2
0 0 0
F values of ANOVAs on aligned responses not of interest (should all be ~0):
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000 0.0000 0.0000 0.1007 0.2199 0.3112
変換したデータを使って分散分析を行ってみる。
anova(henkan)
結果
Analysis of Variance of Aligned Rank Transformed Data
Table Type: Anova Table (Type III tests)
Model: No Repeated Measures (lm)
Response: art(x)
Df Df.res F value Pr(>F)
1 f1 1 18 43.2941 3.5141e-06 ***
2 f2 3 18 22.8532 2.3100e-06 ***
3 f1:f2 3 18 4.4143 0.017077 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
以上から4.1.3と同様に、2つの要因それぞれで各水準間で平均値に差があり、交互作用も認められるといえる。