A Neural Representation of Sketch Drawings
https://arxiv.org/pdf/1704.03477.pdf についてまとめる。
使用している画像は全てこの論文で使用されているものです。
概要
人間が書いた簡単なスケッチのオートエンコーダーを作って、スケッチを生成したり、スケッチ間のアナロジーをしたりといった論文です。かのGoogle Brainの論文なので注目度も高かったものと思います。
(下のデータセットを見ればわかる通り、500万枚以上のスケッチを使っているということで、この規模のデータで実験ができるGoogleが羨ましいです。)
以下、論文の構成に乗っ取ってまとめます。
Methodology
Dataset
オンラインでユーザーが特定のクラスに属するものを20秒で描くデモ The Quickdraw A.I. Experiment(https://quickdraw.withgoogle.com/ )で得られたスケッチのデータを使ってデータセットを作った。データセットには75クラスあり、それぞれにトレーニングデータが7万、validationとテスト用のデータが2,500ある。
Data format
上の図のように、データは点のリストになっていて、それぞれの点は$(\Delta x,\Delta y,p_{1},p_{2},p_{3})$のベクトルで表されている。
$\Delta x,\Delta y$は一つ前の点からのペンの移動距離を表している。$p_{1},p_{2},p_{3}$はそれぞれ、ペンが紙に接触している状態、ペンが紙から離れている状態、書き終わり、を表している。最後の3つはone-hotベクトル表現になっている。
sketch-rnn
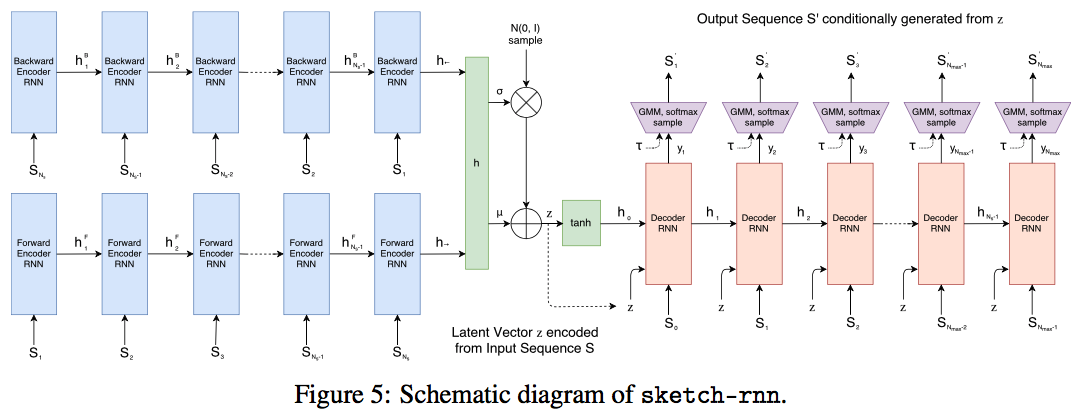
モデルはsequence-to-sequence Variational Autoencoderである。エンコーダーはbidirectional RNNでスケッチを入力としてサイズ$N_{z}$の潜在変数ベクトルを出力する。スケッチの点列$S$と順序を逆にしたもの$S_{reverse}$をそれぞれRNNに入力し、bidirectional RNNを作る。2つの状態が得られるので繋げて$h$を出力する。
h_{\to}=encode_{\to}(S)
h_{\gets}=encode_{\gets}(S_{reverse})
h=[h_{\to};h_{\gets}]
$h$を全結合層に通して、分布の平均$\mu$と標準偏差$\hat{\sigma}$を得る。サイズは$N_{z}$。
$\mu$と$\hat{\sigma}$からIIDガウス分布に従ったランダムベクトル$z\in \mathbb R^{N_{z}}$を得る。(良くあるVAEのアプローチ)
式で書くと、
\mu=W_{\mu}h+b_{\mu}
\hat{\sigma}=W_{\sigma}h+b_{\sigma}
\sigma=exp\Bigl(\frac{\hat{\sigma}}{2}\Bigr)
z=\mu+\sigma\odot\mathcal N(0,I)
潜在ベクトル$z$は入力したスケッチの条件付きランダムベクトルになっている。
デコーダーは自己回帰的RNNで、出力のスケッチを$z$に対して条件付きでサンプリングする。RNNの初期隠れ状態$h_{0}$とセル状態$c_{0}$(使う場合)は単層ネットワークの出力とする。
[h_{0};c_{0}]=tanh(W_{z}z+b_{z})
デコーダーの各ステップiで、前のステップの出力$S_{i-1}$(上の図を参照)と$z$を結合したもの$x_{i}$を入力する。$S_{0}$は$(0,0,1,0,0)$とする。
次の式のように、$(\Delta x,\Delta y)$をM個の正規分布の混合ガウス分布(GMM)でモデル化する。
p(\Delta x,\Delta y)=\sum_{j=1}^{M}\Pi_{j}\,\mathcal N(\Delta x,\Delta y|\mu_{x,j},\mu_{y,j},\sigma_{x,j},\sigma_{y,j},\rho_{xy,j}),\quad where\quad \sum_{j=1}^{M}\Pi_{j}=1\quad -(*)
$\mathcal N$は二変量正規分布である。
また、$(p_{1},p_{2},p_{3})$のモデルとして、$q_{1}+q_{2}+q_{3}=1$を満たす$(q_{1},q_{2},q_{3})$を使う。
式でまとめると、RNNの出力$y_{i}$は、RNNの$forward$操作を用いて、
x_{i}=[S_{i-1};z]
[h_{i};c_{i}]=forward(x_{i},[h_{i-1};c_{i-1}])
y_{i}=W_{y}h_{i}+b_{y},\quad where \quad y_{i}\in \mathbb R^{6M+3}
となる。
$y_{i}$は、
[(\hat{\Pi}_{1}\,\mu_{x}\,\mu_{y}\,\hat{\sigma}_{x}\,\hat{\sigma}_{y}\,\hat{\rho}_{xy})_{1}...(\hat{\Pi}_{1}\,\mu_{x}\,\mu_{y}\,\hat{\sigma}_{x}\,\hat{\sigma}_{y}\,\hat{\rho}_{xy})_{M}\,(\hat{q_{1}}\:\hat{q_{2}}\,\hat{q_{3}})]=y_{i}
を意味するものとする。
標準偏差は正、相関係数は-1から1なので$exp$と$tanh$を施す。
\sigma_{x}=exp(\hat{\sigma_{x}})
\sigma_{y}=exp(\hat{\sigma_{y}})
\rho_{xy}=tanh(\hat{\rho}_{xy})
分類確率は
q_{k}=\frac{exp(\hat{q}_{k})}{\sum_{j=1}^{3}exp(\hat{q}_{j})},\quad k\in \{1,2,3\}
\Pi_{k}=\frac{exp(\hat{\Pi}_{k})}{\sum_{j=1}^{M}exp(\hat{\Pi}_{j})},\quad k\in \{1,...,M\}
として計算する(softmaxですね)。
$\Delta x,\Delta y$は混合ガウス分布の仮定$(*)$に従ってサンプリングする。
描き終わりのトレーニングが難しいが、
デコーダーRNNでトレーニングデータの最大長$N_{max}$の長さの点列を出力するようにして、iが$S$の長さ$N_{s}$を超えた時は$S_{i}=(0,0,0,0,1)$となるようにすることで、ロバストに学習できる。
トレーニング後のサンプリングでは、温度パラメーター$\tau$を導入してランダム性をコントロールする。
q_{k}=\frac{exp(\frac{\hat{q}_{k}}{\tau})}{\sum_{j=1}^{3}exp(\frac{\hat{q}_{j}}{\tau})},\quad k\in \{1,2,3\}
\Pi_{k}=\frac{exp(\frac{\hat{\Pi}_{k}}{\tau})}{\sum_{j=1}^{M}exp(\frac{\hat{\Pi}_{j}}{\tau})},\quad k\in \{1,...,M\}
\sigma_{x}^{2}\to \sigma_{x}^{2}\tau
\sigma_{y}^{2}\to \sigma_{y}^{2}\tau
$\tau$は0から1に設定する。$\tau\to 0$だと決定的になる(ランダム性がなくなる)。
Unconditional Generation
無条件のスケッチ生成モデルも学習した。
エンコーダーを無くしデコーダーRNNのみにして、潜在ベクトルをなくす。RNNの初期隠れ状態とセル状態はゼロにする。
Training
VAEと同じで、ロス関数は2つの項、再構成ロスとKL divergenceロスの和を使う。
再構成ロス$L_{R}$は、$(\Delta x,\Delta y)$のロス$L_{s}$と$(p_{1},p_{2},p_{3})$のロス$L_{p}$の和で表す。
L_{s}=-\frac{1}{N_{max}}\sum_{i=1}^{N_{s}}log\Bigl(\sum_{j=1}^{M}\Pi_{j,i}\;\mathcal N(\Delta x_{i},\Delta y_{i}|\mu_{x,j,i}\,,\mu_{y,j,i}\,,\sigma_{x,j,i}\,,\sigma_{y,j,i}\,,\rho_{xy,j,i})\Bigr)
L_{p}=-\frac{1}{N_{max}}\sum_{i=1}^{N_{max}}\sum_{k=1}^{3}p_{k,i}log(q_{k,i})
L_{R}=L_{s}+L_{p}
KLロス$L_{KL}$は$z$が標準正規分布からどれだけ離れているかを表す。
L_{KL}=-\frac{1}{2N_{z}}\Bigl(1+\hat{\sigma}-\mu^{2}-exp(\hat{\sigma})\Bigr)
従って、ロス関数は
Loss=L_{R}+\mathcal w_{KL}L_{KL}
となる。$\mathcal w_{KL}$は2つの項のロスへの寄与のバランスを決めるスカラー。
$L_{R}$と$L_{KL}$にはトレードオフの関係がある(下図)。
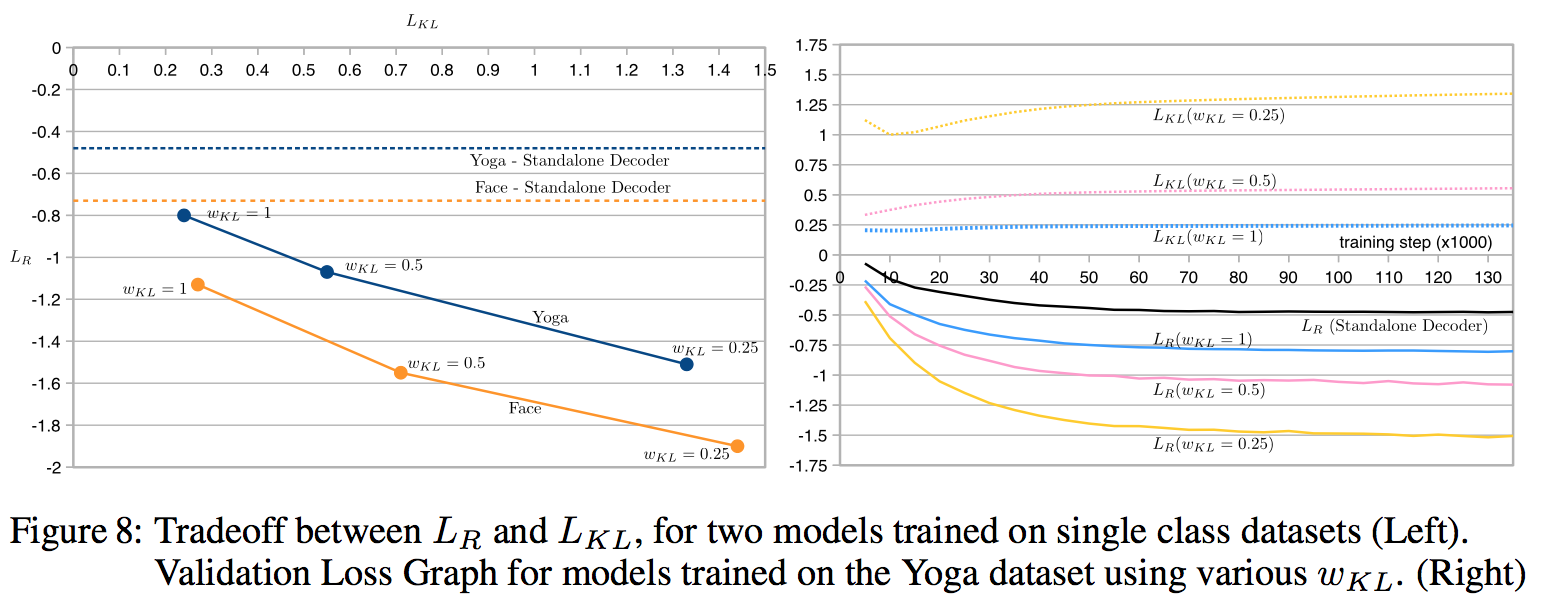
KL項を焼きなます($\mathcal w_{KL}$を徐々に大きくしていく)とロスが小さくなるらしい。なぜなら、最適化が簡単な$L_{KL}$より先に、まず最適化するのが難しい$L_{R}$を最適化するから。上の$Loss$関数を次のように書き換える。
\eta_{step}=1-(1-\eta_{min})R^{step}
Loss_{train}=L_{R}+\mathcal w_{KL}\;\eta_{step}\;max(L_{KL},KL_{min})
$\eta_{step}=\eta_{min}$からスタートする。$\eta_{min}$は0とか0.01とか。
$R$は1に近いが1より小さい値にする。
$KL_{min}$は0.1から0.5くらいで、$L_{KL}$が小さくなりすぎないようにする。
Experiments
sketch-rnnを条件付き(conditional)、条件なし(unconditional)の両方で実験した。学習するクラス数は1クラスから複数クラスまで実験をした。
エンコーダーにはLSTMを、デコーダーにはHyperLSTMを用いた。
各パラメーターは、
$M=20$、$N_{z}=128$、$KL_{min}=0.2$、$R=0.99999$、$\mathcal w_{KL}=1$
トレーニング中$(\Delta x,\Delta y)$はランダムに0.9~1.1倍して、オーグメントした。
Experimental Results
75クラスのうちから選んだ、単独クラス、複数クラスに関して実験をした。
結果は以下の通り。
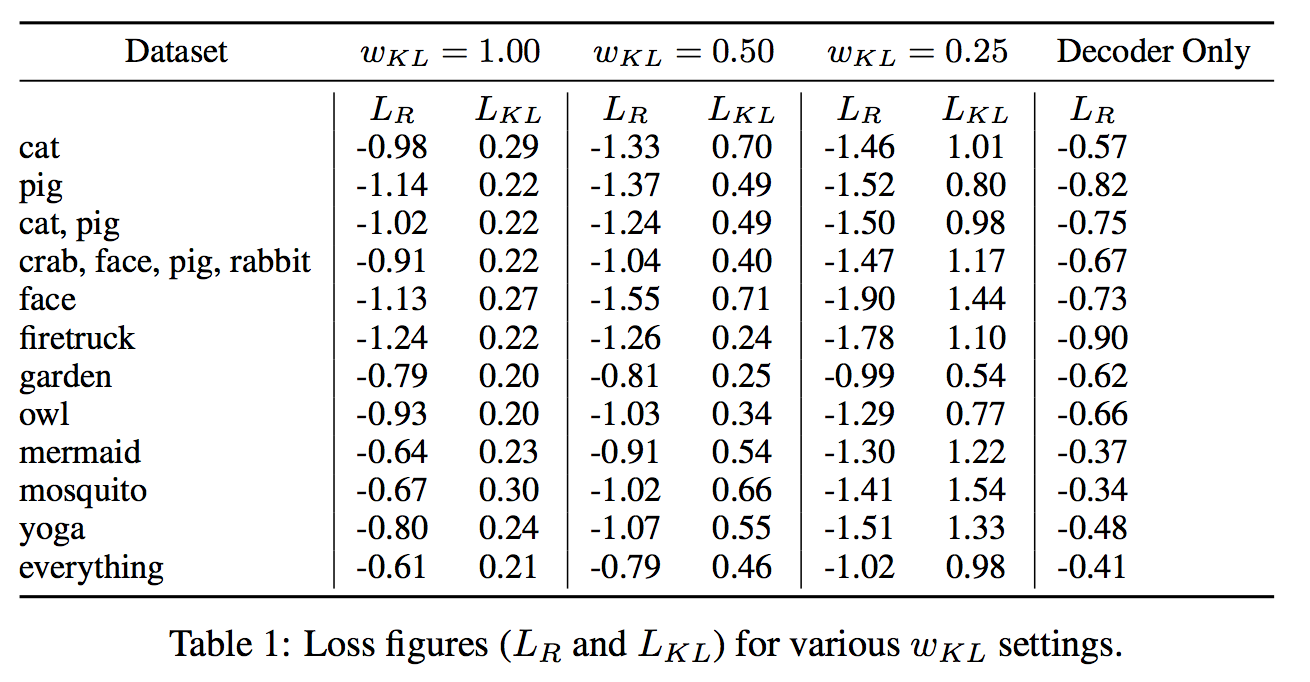
Conditional generation
Conditional Reconstruction
猫クラスでトレーニングしたもので、様々な温度パラメータでの再構成の結果をみてみると、

目が3つの絵を入力しても目が2つの絵が出力されているし、歯ブラシを入力しても猫っぽくなっている!
豚は

脚がたくさんある絵を入力しても脚が2本か4本になるし、トラックを入力しても豚っぽくなる!
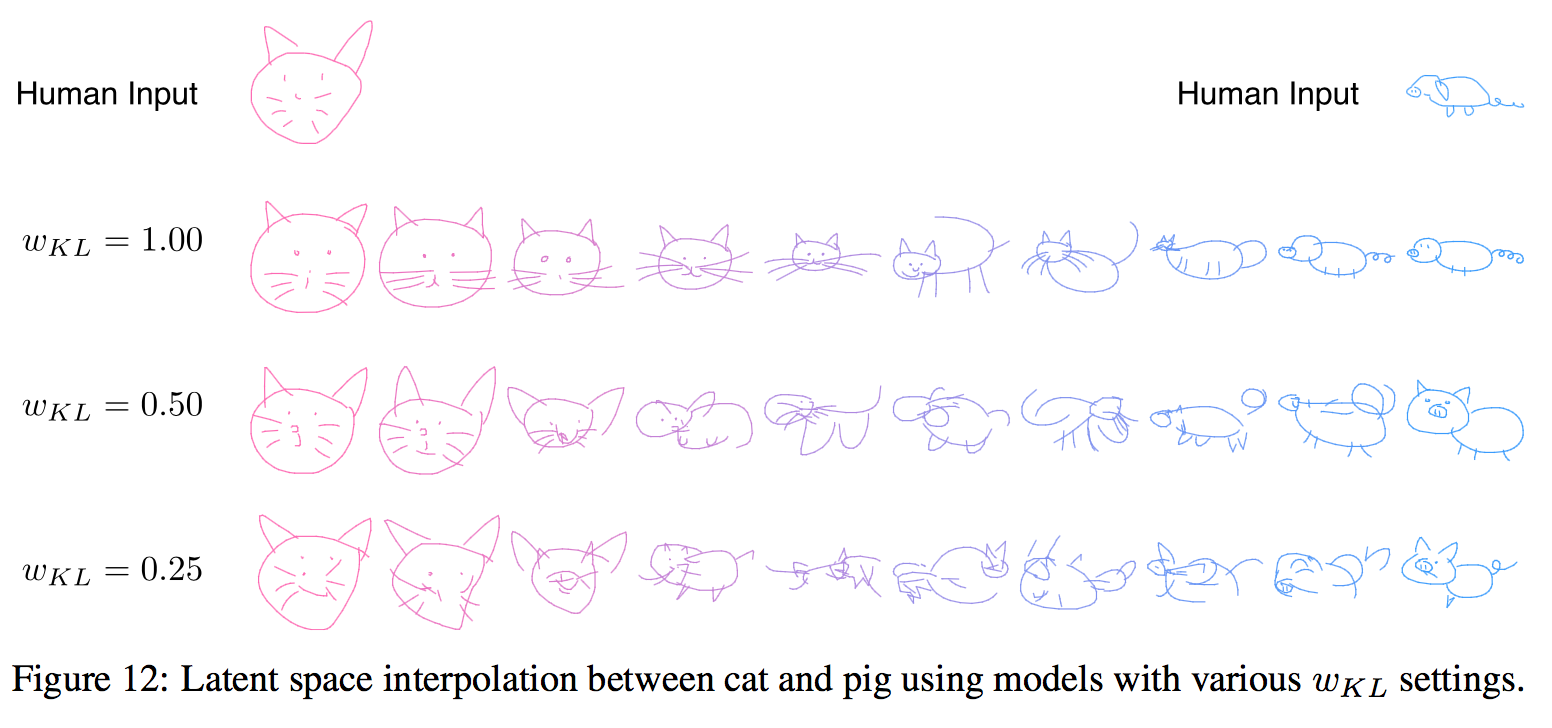
Latent Space Interpolation
Which Loss Controls Image Coherency?
様々な$\mathcal w_{KL}$で再構成してみると、$\mathcal w_{KL}$が大きい方が整合的な出力となっている(下の図)。また、Figure12(上の図)からもわかるように$\mathcal w_{KL}$が大きい方が補間もうまくできている。

Sketch Drawing Analogies
潜在ベクトル$z$に対して足し引きを行ってできたベクトルからスケッチを生成すると、下の図のようにうまくアナロジーができていることがわかる。
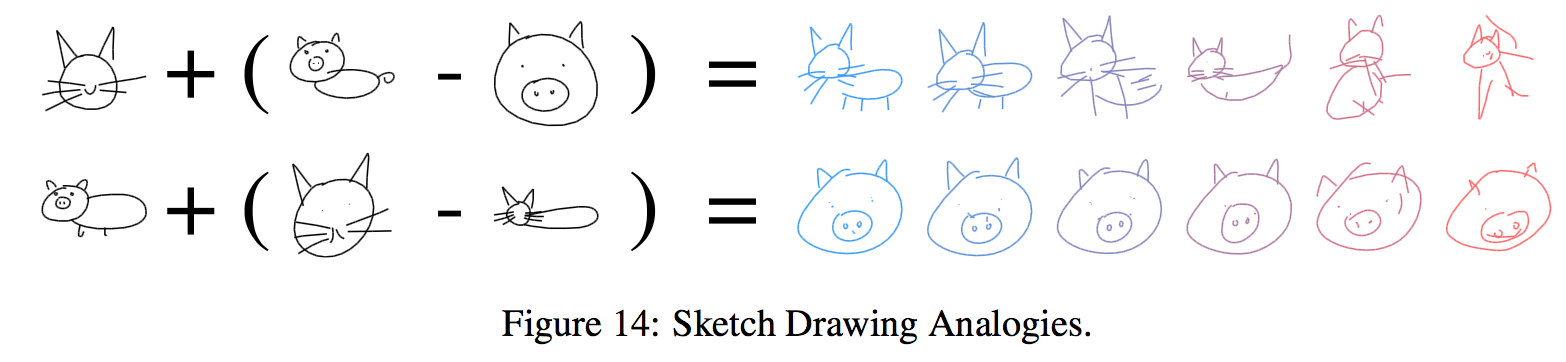
Multi-Sketch Drawing Interpolation

猫で学習したモデルに椅子を入力して、出力同士を補間すると下のようになる。
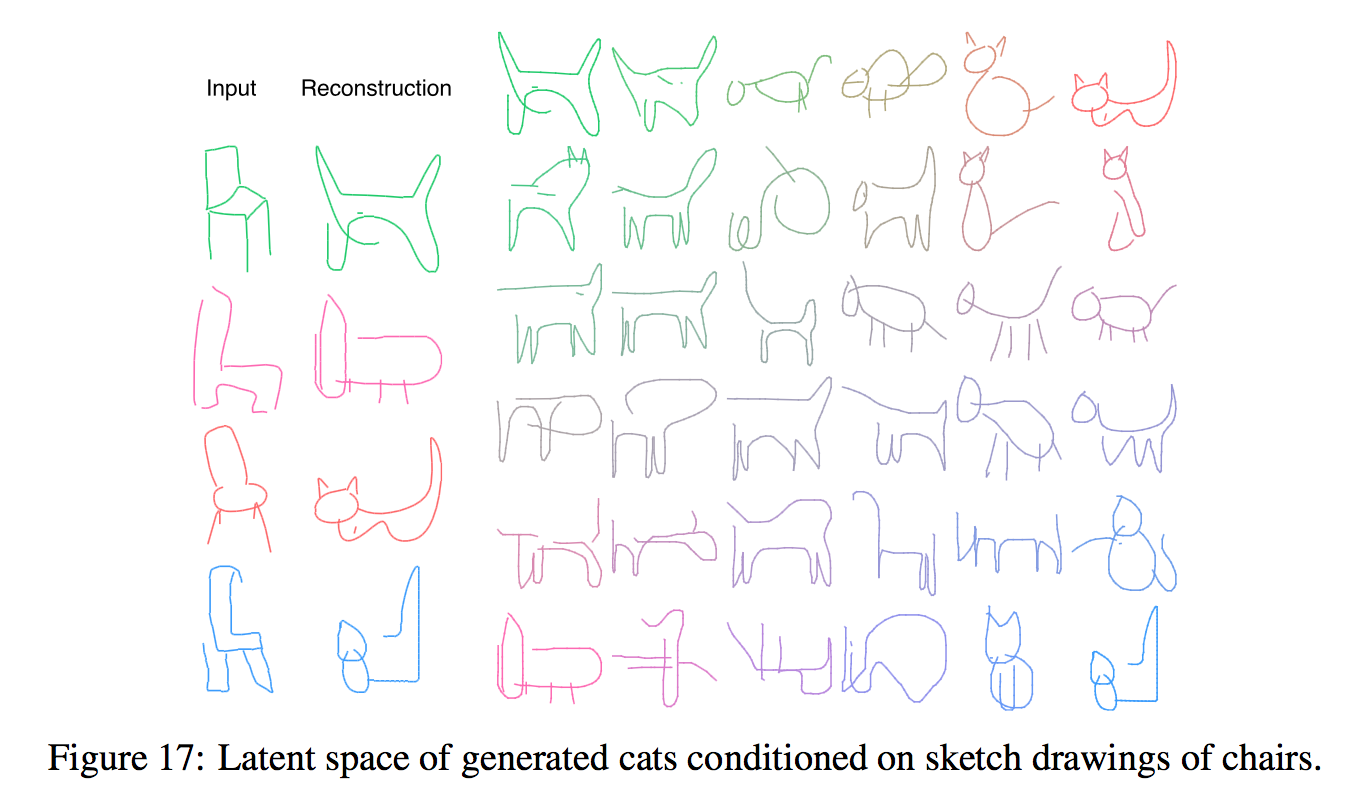
Unconditional generation
デコーダーRNNを単独で使って、入力や潜在ベクトルなしでスケッチを生成する。
$L_{R}$だけ最適化すれば良いので簡単に学習できる。
下の図は、青の$\tau=0.2$から赤の$\tau=0.9$まで様々な$\tau$での生成結果

Predicting Different Endings of Incomplete Sketches
デコーダーRNNを単独で使って、不完全なスケッチを完成させる実験。
うまくいっている。

Discussion
Limitation
このモデルの限界について。
- 単独クラスだと300点列くらいまでモデリングできるが、これ以上の長さだと難しくなる。
- 複雑なクラスは簡単なクラスに比べてロスが大きくなってしまい、出力される絵が滑らかで丸っこいものとなってしまう。(下図)

- 多くのクラスを一気にトレーニングすることはできない。下の図は多くのクラスで学習させたもの。うまく生成できていないことがわかる。

Applications and Future Work
いろんな応用先が考えられる。
- スケッチを完成させるなどアーティストの補助に使える。
- より質の良いモデルが学習できれば、子供に絵の書き方を教えられる。
このモデルは大きなデータセットを学習させるには単純すぎるので、Ladder-VAEsやInverse Autoregressive Flowやganやらも仕組みを応用すればより良くなるかも。
教師なしと組み合わせるのも面白そう。
Conclusion
RNNでスケッチをモデリングする方法を開発した。
未完成のスケッチを完成させることができる。
スケッチを潜在ベクトルにエンコードするのにも使える。
スケッチ間の補間もできる。
特定のクラスでトレーニングすれば、入力の間違った特徴を直せる。
潜在空間の拡張によりスケッチの属性を操作する(?)ことができたし、整合的なベクトル画像生成には潜在ベクトルの事前分布を考えることが重要だとわかった。
以上