Modeling Relational Data with Graph Convolutional Networksのまとめ

Modeling Relational Data with Graph Convolutional Networks
https://arxiv.org/pdf/1703.06103.pdf についてまとめる。

概要

• 現実的な知識ベースに特徴的な、多くの関係性を持ったデータを扱うために開発された。Graph Convolutional Networks(GCNs)の一般形。
• relational graph convolutional networks(R-GCNs)を紹介し、2つの知識ベース完成タスクに適用する。
  • Link prediction
    • 与えられた不完全なグラフに対して、明らかでないエッジ(ノード同士の関係)を予測するタスク
  • Entity classification
    • ノードの属性を予測するタスク

グラフについて

グラフ$G=(\mathcal V,\mathcal E,\mathcal R)$を考える。
ノード$v_{i}\in \mathcal V$、エッジ同士の関係のタイプ$r\in \mathcal R$、ラベルのついたエッジ$(v_{i},r,v_{j})\in \mathcal E$とする。
ノードの情報は属性に対するone-hotベクトルとして表現する。(例えばノードが単語を表すとすれば、単語のone-hotベクトル)

Graph Convolutional Networks(GCNs)とは

画像を入力できるのがConvolutional Neural Networkなら、グラフをそのまま入力できるネットワークがGraph Convolutional Networkである。

Relational Graph Convolutional Network(R-GCN)

R-GCNの各層では、エッジの種類と方向を考慮して情報が伝播していく。各層は下のような構成になっている。

h^{(l+1)}_{i}=\sigma\Bigl(\sum_{r\in\mathcal R}\sum_{j\in\mathcal N^{r}_{i}}\frac{1}{\mathcal c_{i,r}}W^{(l)}_{r}h^{(l)}_{j}+W^{(l)}_{0}h^{(l)}_{i}\Bigr)

ここで、$h_{i}^{(l)}\in\mathbb R^{d^{(l)}}$はノード$v_{i}$のl層目の隠れ層の状態、$d^{(l)}$はl層目の表現の次元、$\sigma$は非線形活性化関数、$c_{i,r}$は問題に固有の正規化定数である。$\mathcal N_{i}^{r}$は$r\in\mathcal R$関係下でのノードiの隣接ノードのインデックスを表す。

この式の意味するところは、それぞれのノード$v_{i}$に対して、グラフの結合関係からl層目の隠れ層の状態$h_{i}^{(l)}$を計算し、その情報が次の層に伝わって行くということである。

$W_{r}^{(l)}$は

W_{r}^{(l)}=\sum_{b=1}^{B}a_{rb}^{(l)}V_{b}^{(l)}

のように基底変換$V_{b}^{(l)}\in\mathbb R^{d^{(l+1)}\times d^{(l)}}$と係数$a_{rb}^{(l)}$(スカラー)の積で表される。(Bは基底関数の数を表す。)
正規化係数$c_{i,r}$(例えば$c_{i,r}=|\mathcal N_{i}^{r}|$)を導入することで、グラフ全体で同じようなスケールのアクティベーションができるようになる。これにより、グラフの大きさによらないモデリングが可能となる。

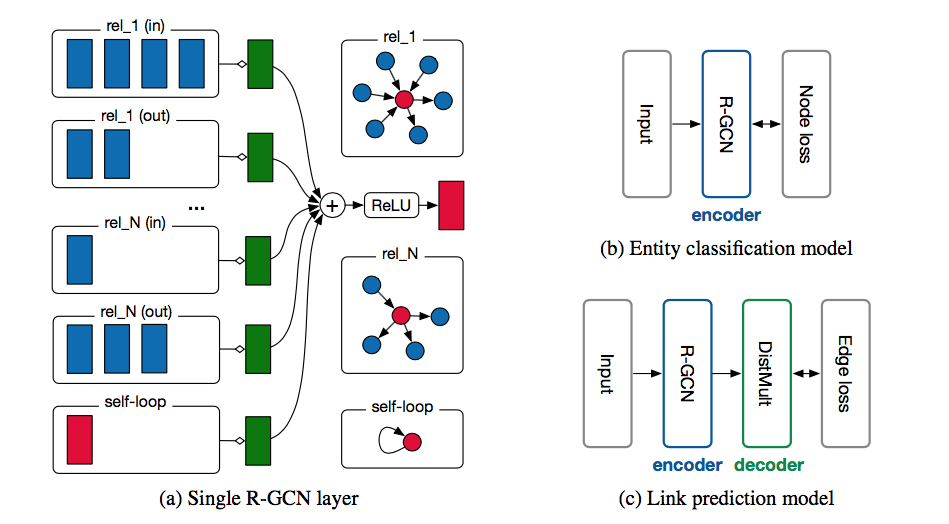
(https://arxiv.org/pdf/1703.06103 より)
上の図(a)はR-GCNの構造を示している。
この図について説明すると、
赤く示されているものが、今注目しているノード(上の式だと$v_{i}$)を表している。
それぞれの関係(向きも考慮して)について、その関係性により$v_{i}$と結合しているノード(青で表現されている)を取り出し、それらのノードの隠れ層の状態の和をとる。

\sum_{j\in\mathcal N^{r}_{i}}h^{(l)}_{j}

それぞれの関係に対して定義された重みを掛ける。(緑の層)

\sum_{j\in\mathcal N^{r}_{i}}\frac{1}{\mathcal c_{i,r}}W^{(l)}_{r}h^{(l)}_{j}

全ての関係について(self loopも含めて)足し合わせる。(緑から出た矢印)

\sum_{r\in\mathcal R}\sum_{j\in\mathcal N^{r}_{i}}\frac{1}{\mathcal c_{i,r}}W^{(l)}_{r}h^{(l)}_{j}+W^{(l)}_{0}h^{(l)}_{i}

2項目はself loopを表す。

あとは、活性化関数を施せば、上で示した構成式と同じになる。//

$V_{b}^{(l)}\in\mathbb R^{d^{(l+1)}\times d^{(l)}}$と$a_{rb}^{(l)}$は、CNNでフィルターのパラメーターが画像全体で共有されるように、グラフ全体で共有される。

モデルでは、l層目の出力がl+1層目に入力される。最初の層の入力は各ノードについてのone-hotベクトルとする。

最終層の出力をR-GCNの出力とする。

Link prediction

Link predictionでは、不完全なグラフ(ノード間の関係が全て明らかになっているわけではないグラフ)に対して、明らかになっていない新しい関係を予測する。つまり、ノードsubjectとobjectの間の関係を表すエッジ (subject, relation, object) を予測する。
可能性のあるエッジ(s,r,o)に対してスコアf(s,r,o)を割り当てることで、そのエッジがどれくらい関係性を反映しているかを決める。

どうするかというと、エンコーダーと評価関数(デコーダー)を組み合わせたグラフオートエンコーダ作る。エンコーダーは各ノード$v_{i}\in \mathcal V$をベクトル$e_{i}\in\mathbb R^{d}$に写像する。デコーダーはエッジ(subject, relation, object)を評価する。つまり、$\mathbb R^{d}\times\mathcal R\times\mathbb R^{d}\to\mathbb R$のような写像をする関数である。

論文の実験では、エンコーダーとしてR-GCNを用い、$e_{i}=h_{i}^{(L)}$とし、デコーダーとしてDistMultを用いている。DistMultは単独でリンク予測ベンチマークで良い性能を発揮することが知られている。DistMultでは各関係$r$に対して行列$R_{r}\in\mathbb R^{d\times d}$を割り当て、(s,r,o)を

f(s,r,o)=e_{s}^{T}R_{r}e_{o}

によって評価する。

コスト関数は交差エントロピー

\mathcal L=-\frac{1}{(1+\omega)|\hat{\mathcal E}|}\sum_{(s,r,o,y)\in\mathcal T}y\,log\,\sigma(f(s,r,o))+(1-y)log(1-\sigma(f(s,r,o)))

を使う。
$\omega$はネガティブサンプルの割合で、ポジティブ例からランダムにobjectとsubjectを選んでネガティブデータを作る。
$\hat{\mathcal E}$はグラフの不完全なエッジ集合を表す。$\mathcal T$は(s,r,o)の組の全体、$\sigma$はロジスティックシグモイド関数、$y$はポジティブ(関係がある)なら1ネガティブ(関係がない)なら0となる数である。
上図の(c)がモデルの構造を表している。

Entity classification

ノード(エンティティ)分類の(半)教師あり学習。単純にR-GCN層を積み重ね、出力にsoftmaxを使う。
以下の交差エントロピーを用いて評価する。

\mathcal L=-\sum_{i\in\mathcal Y}\sum_{k=1}^{K}t_{ik}\,ln\,h_{ik}^{(L)}

$\mathcal Y$はラベルのついたノードの集合、$h_{ik}^{(L)}$はネットワークの出力のノードiのk番目のエントリーの値、$t_{ik}$はラベル(0 or 1)を表す。
構造は上図の(b)。

結果

Link prediction

WordNet(WN18)データセットとFreebase(FB15)データセットで評価した。
正規化係数として$c_{i,r}=c_{i}=\sum_{r}|\mathcal N_{i}^{r}|$を用いた。

R-GCNとDistMultを組み合わせたモデルR-GCN+

f(s,r,t)_{R-GCN+}=\alpha\,f(s,r,t)_{R-GCN}+(1-\alpha)f(s,r,t)_{DistMult}

も定義して評価した。

結果(https://arxiv.org/pdf/1703.06103.pdf より)

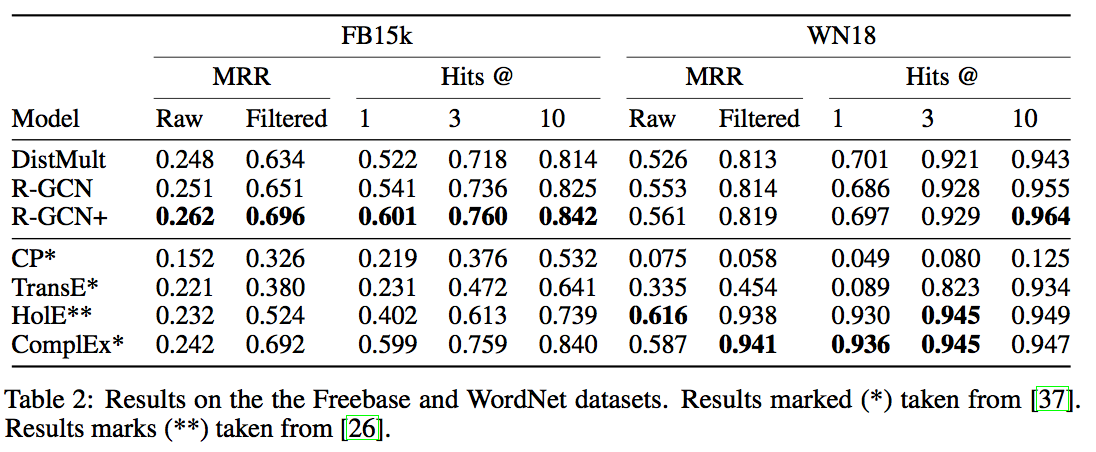
Freebaseデータセットに対しては、R-GCNとR-GCN+は既存手法より性能が良く、R-GCN+の方がより良かった。
WornetではR-GCN+の方がR-GCNより良かったとはいえ、既存手法とあまり変わらなかった。

Entity classification

3つの知識グラフデータセット、AIFB、MUTAG、BGSで評価した。
正規化係数には$c_{i,r}=|\mathcal N_{i}^{r}|$を用いた。

結果(https://arxiv.org/pdf/1703.06103.pdf より)

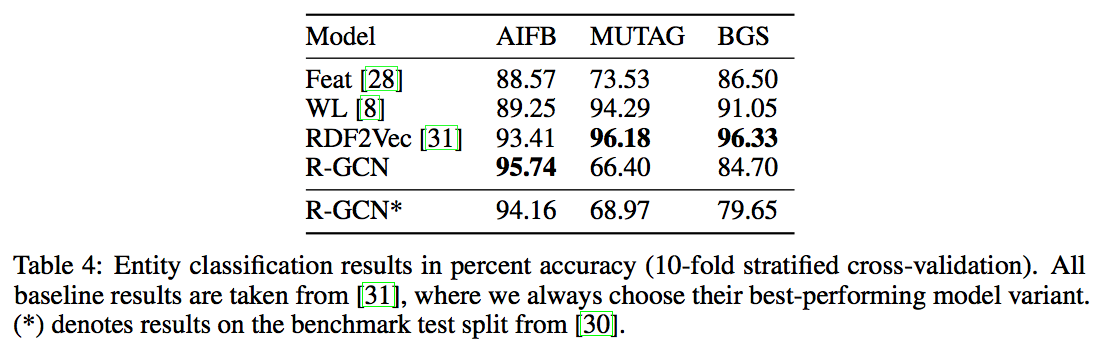
AIFBしか既存手法と同じくらいの性能にならなかった。
他の2つに対しては正規化係数を変えると性能が向上する可能性がある。