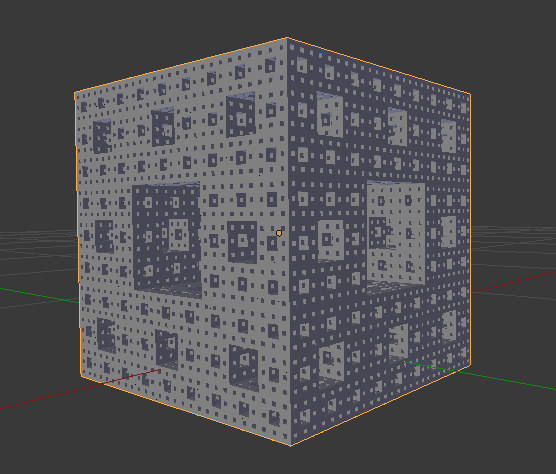
結論
筆者のスペック
・非情報系
・3Dモデルいじったことない
・もちろんblenderもほとんど初めて
こんなのでもできるのでかんたんだよ!
ここでつくるもの
上記の「シェルピンスキーのギャスケット」の3次元版を作ります
やりかた
blenderの画面がいくつか分割されていると思いますが、この中の切替の中から、「pythonコンソール」を選べば対話的に実行できます。
ただ、これでは出来ないことも多いので、おすすめは「テキストエディター」を選んでやると、下のようなものが出るよ!
ここ下にある「新規」ボタンを押す。これだけで準備は完了です。
コード
記法については色々有るのですが、基本的にかんたんです。
まず全体を見てみましょう。
import bpy
from math import sqrt
def duplicate_object_rename(arg_objectname='Default', arg_dupname='', position=(0,0,0)):
for ob in bpy.context.scene.objects:
ob.select=False
selectob=bpy.context.scene.objects[arg_objectname]
#bpy.context.scene.objects.active = selectob
selectob.select=True
bpy.ops.object.duplicate_move(
OBJECT_OT_duplicate=None, TRANSFORM_OT_translate=None)
# move object
bpy.ops.transform.translate(value=position)
selectob.select=False
if len(arg_dupname) > 0:
duplicated_objectname=arg_objectname + ".001"
duplicatedob=bpy.data.objects[duplicated_objectname]
duplicatedob.name=arg_dupname
return
scale = 0.01
bpy.ops.mesh.primitive_cone_add(vertices=3,radius1=1*scale,depth=sqrt(2)*scale,location=(scale*sqrt(3)*(.5+.5*1+1),scale*1.5*(1+3*1)/3,scale*sqrt(2)/2),rotation=(0,0,0))
duplicate_object_rename(arg_objectname='Cone', arg_dupname='Duplicate1',position=(scale*sqrt(3),0,0))
duplicate_object_rename(arg_objectname='Cone', arg_dupname='Duplicate2',position=(scale*sqrt(3)/2,scale*1.5,0))
duplicate_object_rename(arg_objectname='Cone', arg_dupname='Duplicate3',position=(scale*sqrt(3)/2,scale*1/2,scale*sqrt(2)))
bpy.ops.object.select_by_type(type = 'MESH')
bpy.ops.object.join()
namehead = 'Duplicate'
for i in range(1,7):
namebufprev = namehead + str(i)
namebuf = namehead + str(i+1)
duplicate_object_rename(arg_objectname=namebufprev, arg_dupname=namebuf,position=(scale*sqrt(3)*2*2**(i-1),0,0))
duplicate_object_rename(arg_objectname=namebufprev, arg_dupname='buf2',position=(scale*sqrt(3)*2**(i-1),scale*3*2**(i-1),0))
duplicate_object_rename(arg_objectname=namebufprev, arg_dupname='buf3',position=(scale*sqrt(3)*2**(i-1),scale*2**(i-1),scale*2*sqrt(2)*2**(i-1)))
bpy.ops.object.select_by_type(type = 'MESH'))
bpy.ops.object.join()
bpy.ops.object.origin_set(type = 'ORIGIN_GEOMETRY', center = 'MEDIAN')
順繰り説明していきます
1.ライブラリ
import bpy
from math import sqrt
ここでbpyというモジュールをインポートしてますが、これがblenderの関数です。これらはpipとか使わなくても最初からインストールされていますので、何も考えずインポートしてしまいましょう。この他にも基本的なモジュールは最初から含まれています。ここでは、三角形の重心位置などを求めるために平方根を取らなければならなかったので、mathをインポートしています。
pandasなどは入っていません。自力でインストールしようと思えば出来ますが、ここでは取り扱いません。
2.メソッド
して、どうやるの?って話になると思いますが、実はもう答えは用意されています。blenderをいじるとポップアップでコードが出てくるんですが、これがその操作に相当するメソッドに当たります。例えば
bpy.ops.mesh.primitive_cone_add(vertices=3,radius1=1*scale,depth=sqrt(2)*scale,location=(scale*sqrt(3)*(.5+.5*1+1),scale*1.5*(1+3*1)/3,scale*sqrt(2)/2),rotation=(0,0,0))
ですがこれはプリミティブ図形の円錐に相当します。ポップアップだけでだいたい分かるので自分で部分的に作ってみる→自動化するの流れになるかと思います。ですので、blenderを自在に操れる方はさほど困難はないでしょうし、そうでない方はコーディングよりも操作の方で引っかかると思います。
3.記法
これについてはほとんど普通のpythonと代わりありません。強いて言えば、デバッグの際に何が悪いのかわかりにくいので、根気よくデバッグしてください。意外とメモリを食うので、うまく書かないと動作が低速になりがちです。今回もそれなりのPCを使っているにも関わらずすぐに出力されるのではなく、一拍おいてから出力されます。
4.VCI化
あとはfbx出力してunityに突っ込むだけ、、、なんですがその前に一つ注意
vciにした際には、subitemの個数が多すぎると急激に重くなるみたいで、自分の環境では800も入れればがくがくになってしまいます。そして、フラクタルは階数が触れるだけで急激にオブジェクト数が増えます。(今回は7階ですが、まとめないとバーチャルキャストが落ちます。。。。)ですので、作ったオブジェクトは最後に一つにまとめておいたほうがいいです。
まとめるには
bpy.ops.object.select_by_type(type = 'MESH')
bpy.ops.object.join()
などが便利でしょう。
サイズが重くても読み込みが重いだけで動作はあまり遅くなりませんが、オブジェクト数が多いと動作も重くなる上に、場合によってはthe seed onlineのアップロードがはねられます。その際のエラーメッセージは「chunk sizeが大きすぎます」だったかな。
発展
参考
本記事はほとんどこちらの二番煎じのようなものです
こちらではコッホの雪片の3次元版をやられていますね
https://qiita.com/hoji1107/items/99b2b669225d05990b5b
こちらのコードを改造しながら勉強させていただきました。
フラクタル自体の説明はこちら
https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%A9%E3%82%AF%E3%82%BF%E3%83%AB
シェルピンスキーのギャスケットについては英語版のほうがいいかな
https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle