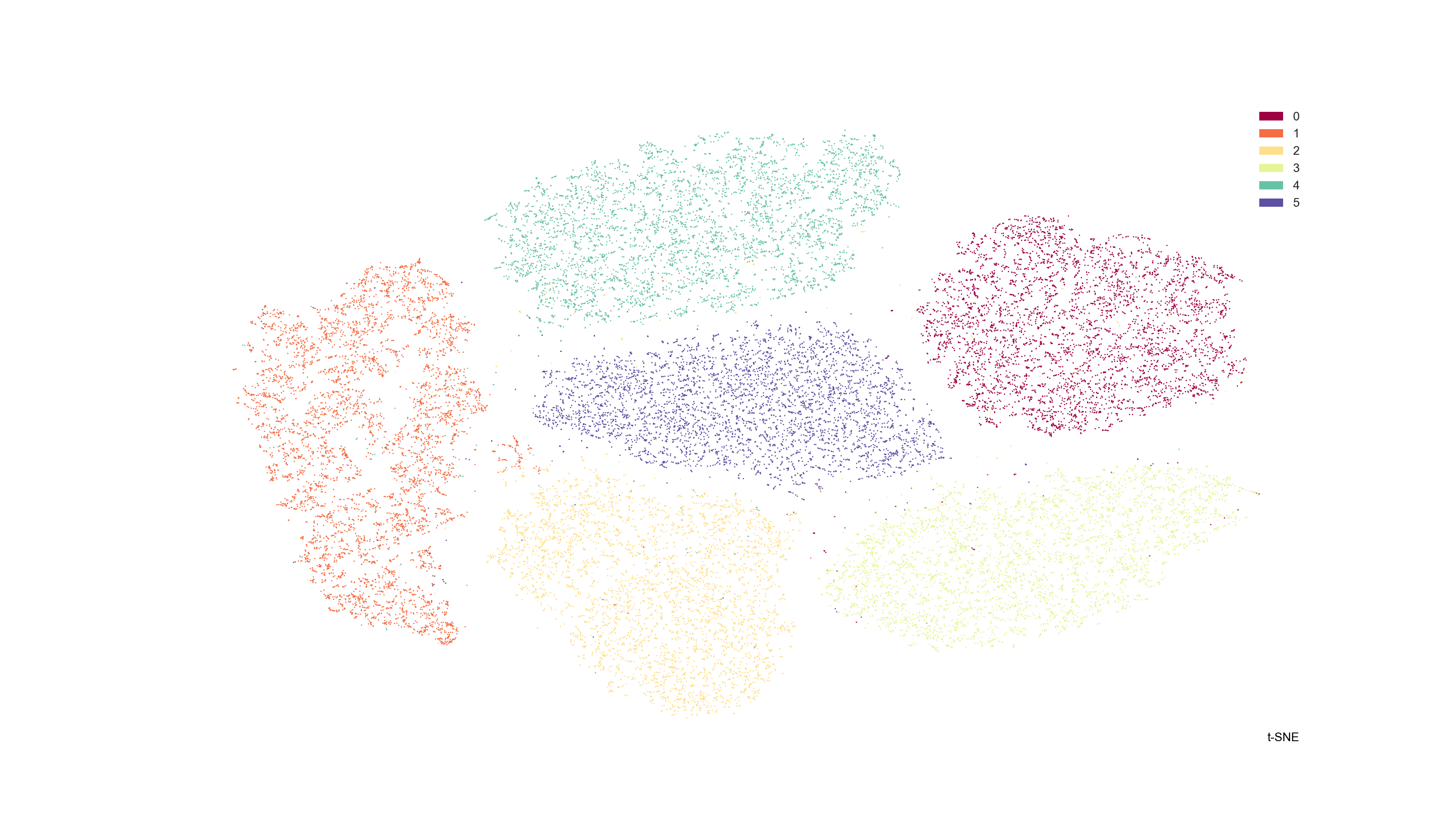Visualizing Data using t-SNE をまとめます。
- t-SNE とは
- SNE (Stochastic Neighbor Embedding)
- t-SNE (t-Distributed Stochastic Neighbor Embedding)
- 大規模データへの適用
- t-SNE の弱点
t-SNE とは
t-SNE は、次元圧縮の手法で、特に可視化に用いることを意図しています。
データの局所的な構造をうまく捉えることができるだけでなく、さまざまなスケールのクラスタなど、大域的な構造も保った可視化ができる点が特徴です。
SNE (Stochastic Neighbor Embedding)
最初に、t-SNE の基となる手法である SNE (Stochastic Neighbor Embedding) を紹介します。
SNE では、元の空間での点同士の近さが、圧縮後の点同士の近さとできるだけ同じになるように次元を圧縮します。
ここで、点 $i$ から点 $j$ への「近さ」とは、以下で定義されます。
p_{j \mid i}=\frac{\exp \left(-d_{ij}^{2}\right)}{\sum_{k \neq i} \exp \left(-d_{ik}^{2}\right)} \tag{1}
$d_{ij}$ は点 $i$ と点 $j$ の「距離」を表します。つまり、全体の距離を用いて正規化されたものを「近さ」と呼んでいます。
SNE では、この「距離」として、元の空間と圧縮後の空間で異なるものを用いています。
元の空間の点 $\boldsymbol{x}_i$, $\boldsymbol{x}_j$ が、圧縮後の空間での点 $\boldsymbol{y}_i$, $\boldsymbol{y}_j$ に対応するとして、元の空間では、
d_{ij}^2 = \frac{\left\|\boldsymbol{x}_i - \boldsymbol{x}_j\right\|^2}{2\sigma_i^2} \tag{2}
圧縮後の空間では、
d_{ij}^2 = \left\|\boldsymbol{y}_i - \boldsymbol{y}_j\right\|^2 \tag{3}
となります。ここで、元の空間での距離の分母の $\sigma_i$ は、点 $i$ ごとに異なる値をとります。
この $\sigma_i$ は、「どれだけ $i$ の近くの点を重要視するか」を表すパラメーターになります。
式 $(2)$ を式 $(1)$ に代入すると、
p_{j \mid i}=\frac{\exp \left(-\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{j}\right\|^{2} / 2 \sigma_{i}^{2}\right)}{\sum_{k \neq i} \exp \left(-\left\|\boldsymbol{x}_{i}-\boldsymbol{x}_{k}\right\|^{2} / 2 \sigma_{i}^{2}\right)}
つまり、正規分布の平均を点 $i$ においたときの確率値の割合になっています。
このとき、 $\sigma_i$ が大きければ大きいほど、遠くの点が重要視されます。
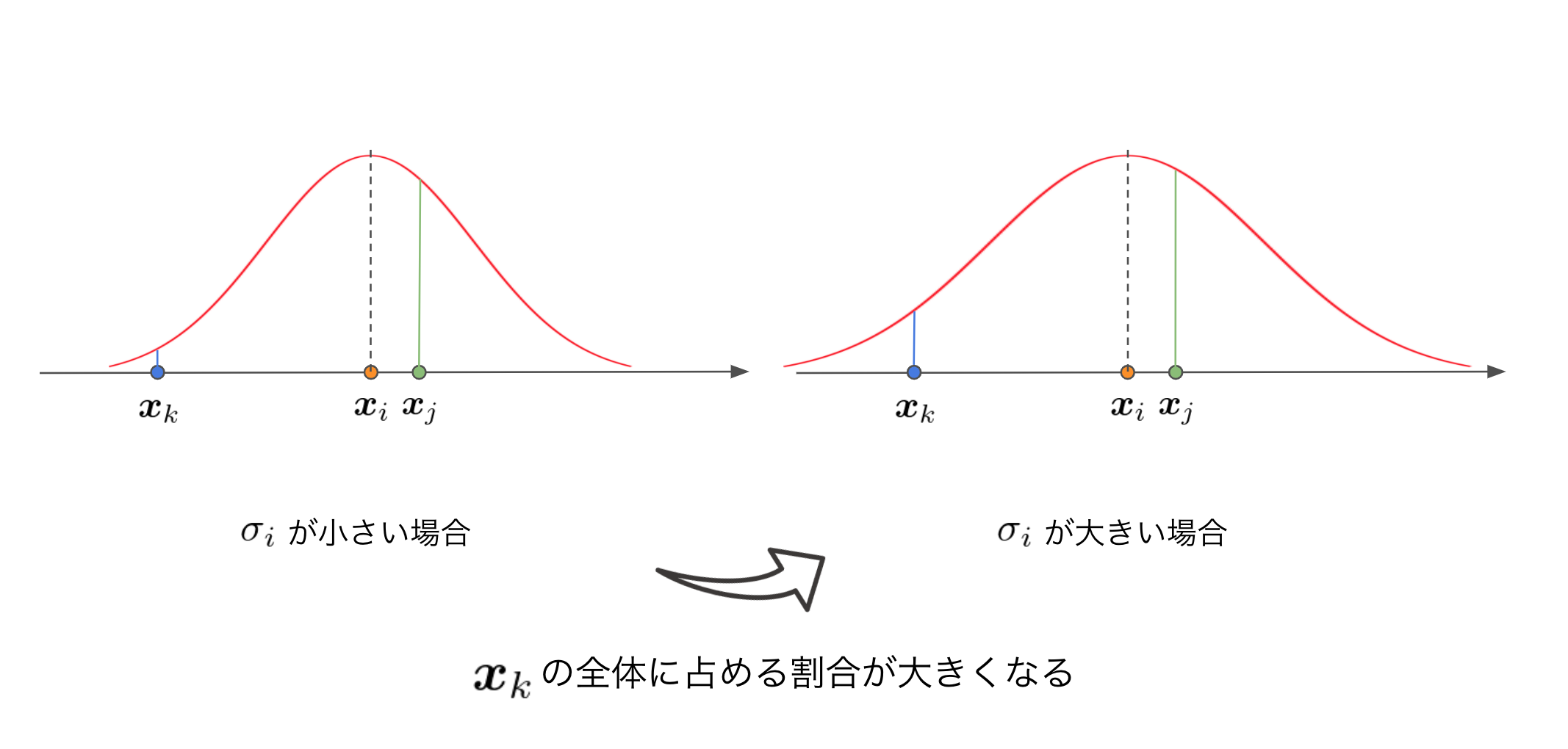
この $\sigma_i$ を、すべての点でエントロピーが一定になるように定めます。エントロピーは以下の式で表されます。
H\left(P_{i}\right)=-\sum_{j} p_{j \mid i} \log _{2} p_{j \mid i}
点が密集している部分の $i$ では $\sigma_i$ を小さく抑え (= $p_{j \mid i}$ を小さく抑え) 、エントロピーが大きくなりすぎないようにします。
点が密集している部分では局所的な構造を、点がまばらになっている部分では全体的な構造を捉えて圧縮することで、きれいな可視化ができる、というわけです。
ちなみに、ユーザーが与えるパラメーターはエントロピーそのものではなく、パープレキシティと言って、
\operatorname{Perp}\left(P_{i}\right)=2^{H\left(P_{i}\right)}
の値を指定します。5から50までの値を指定するのがよいようです。
さて、「近さ」が定義できたので、次はそれらをできるだけ同じにするようなアルゴリズムを導出します。
SNE では、元の空間での「近さ」 $p_{i \mid j}$ に対して、圧縮後の空間での「近さ」を $q_{i \mid j}$ として、すべてのデータ点の Kullback-Leibler divergence の合計を最小化します。コスト関数 $C$ は以下で与えられます。
C=\sum_{i} K L\left(P_{i} \| Q_{i}\right)=\sum_{i} \sum_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}} \tag{4}
$P_i$ は、元の空間でデータ点 $\boldsymbol{x}_i$ が与えられたときの、その他すべてのデータ点の条件付き確率分布、$Q_i$ は、圧縮後の空間でデータ点 $\boldsymbol{y}_i$ が与えられたときの、その他すべてのデータ点の条件付き確率分布を表します。
このコスト関数を最小化するため、モーメンタム付きの勾配降下法を使用します。
\mathcal{Y}^{(t)}=\mathcal{Y}^{(t-1)}+\eta \frac{\delta C}{\delta \mathcal{Y}}+\alpha(t)\left(\mathcal{Y}^{(t-1)}-\mathcal{Y}^{(t-2)}\right)
ここで $\mathcal{Y}^{(t)}$ は時刻 $t$ における圧縮後の各点の値、 $\eta$ は学習率、 $\alpha(t)$ は時刻 $t$ でのモーメンタムを表します。
圧縮後のデータ点は等方的な正規分布で初期化され、上の更新式により学習されます。また、学習初期では更新後の値にガウシアンノイズを加えます。このノイズを除々に小さくしていくことで、一種の焼きなましのように作用して、局所解から脱出しやすくなります。
しかしこの方法は、学習初期に加えるノイズの大きさや、その減衰率に対してとても敏感です。さらにそれらが、モーメンタムやステップサイズにも関係してくるので、適切なパラメーターを探索するために複数回の学習を回す必要があります。
t-SNE (t-Distributed Stochastic Neighbor Embedding)
SNE は可視化としてはそこそこうまくいくのですが、問題点として、次の2点があります。
- コスト関数の最適化が困難
- Crowding Problem
Crowding Problem は、データの次元を圧縮すると、近傍の点を中心に強く集めて押し潰してしまう問題のことです。
例えば、元の空間で互いに等距離に配置された3個の点を1次元に圧縮したい、という状況を考えます。このとき、アルゴリズムによる更新をすると、3つの点すべてを同一の場所に配置することで「互いに等距離」を実現しようとします。圧縮後の点を更新する際に及ぼされるこうした引力は、等間隔に存在する他のすべての点から発生するため、合計すると非常に大きくなってしまいます。そのため、近傍の点を正確に再現しようとしすぎるあまり、それらを中心に集めようという強い引力が発生し、自然なクラスタを形成する妨げになってしまいます。
そこで、これらの問題点を解決するのが t-SNE (t-Distributed Stochastic Neighbor Embedding) です。
t-SNE は、SNE と次の2つの点で異なっています。
- 対称なコスト関数を使用
- 圧縮後の空間の「近さ」の計算に Student-t 分布を使用
順番に説明していきます。
1. 対称なコスト関数を使用
t-SNE では、対称なコスト関数を導入します。
SNE では、条件付き確率分布 $p_{j \mid i}$ と $q_{j \mid i}$ の KL-divergence の合計を最小化していましたが、t-SNE では同時確率分布 $p_{ij}$ と $q_{ij}$ の KL-divergence の合計を最小化します。
C=K L(P \| Q)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} \tag{5}
この場合の「近さ」は点 $i, j$ 間で対称になるので、 symmetric SNE と呼びます。
ただしこのとき、単純に同時確率分布を使用すると、元の空間で点 $i$ が外れ値だった場合、 $p_{ij}$ がすべての点 $j$ について非常に小さくなってしまい、コスト関数への寄与がなくなって、圧縮後の空間へのマップがうまくいかなくなってしまいます。
そこで、元の空間の「近さ」については次のように置き換えます。
p_{ij} = \frac{p_{j \mid i} + p_{i \mid j}}{2n}
圧縮後の空間の「近さ」については同時確率分布を適用し、
q_{i j}=\frac{\exp \left(-\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)}{\sum_{k, l \neq k} \exp \left(-\left\|\boldsymbol{y}_{k}-\boldsymbol{y}_{l}\right\|^{2}\right)}
となります。
2. 圧縮後の空間の「近さ」の計算に Student-t 分布を使用
SNE では、Crowding Problem という、圧縮後の点に必要以上に引力が発生して、点が「混み合ってしまう」問題が発生しています。
Crowding Problem を緩和するため、t-SNE では、圧縮後の確率分布に自由度1の Student-t 分布を採用します。

この分布を用いることで、注目している点の近傍の確率分布がなだらかになり、点が集まる箇所の近くに余剰空間を作り出すことができます。
このとき、圧縮後の確率分布は以下のようになります。
q_{i j}=\frac{\left(1+\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)^{-1}}{\sum_{k, l \neq k}\left(1+\left\|\boldsymbol{y}_{k}-\boldsymbol{y}_{l}\right\|^{2}\right)^{-1}} \tag{6}
この値は、指数関数を用いないため、正規分布に比べてはるかに高速に計算することができます。
t-SNE の利点
以下に、SNE および t-SNE の、勾配を表すヒートマップを示します。勾配が正のときは引力、負のときは斥力が働きます。
横軸が元の空間での距離、縦軸が圧縮後の空間での距離を表します。例えば SNE では、元の空間での距離が小さいが、圧縮後の空間で距離が遠くなっているときに大きな引力が働きます。

この図から、t-SNE では、元の空間で遠くに存在した点同士を圧縮後の空間で近くにマップした場合に、斥力が働くことがわかります。SNE でもそうした斥力は存在するのですが、その大きさは他の点の引力に比べて弱くなってしまいます。
まとめると、t-SNE は、「距離が離れたデータ点同士を似ていない点としてモデル化」し、かつ、「距離が近いデータ点同士を似た点としてモデル化」することができます。この性質から、t-SNE のコスト関数は、SNE のものに比べてはるかに最適化しやすいものになっています。
t-SNE の最適化手法
t-SNE では、圧縮後のデータ点は SNE と同様に、等方的な正規分布で初期化され、モーメンタム付きの勾配降下法により学習されます。ただし、学習初期のノイズによる焼きなましは行いません。
これだけでも t-SNE は他の手法よりも優れた結果を示すのですが、次の2つのテクニックを使用することで、さらに結果を改善することができます。
- early compression
early compression は、学習初期に各点を互いに近くに配置するテクニックです。
これにより、クラスタ同士の斥力を介してデータの大域的な構造を探索しやすくなります。直感的にも、離れた点からクラスタを形成するよりも、近くのクラスタ同士が分かれるほうが簡単なことがわかると思います。
アルゴリズム上は、コスト関数に原点からの距離を l2 正則化項として追加することで実装します。正則化項の大きさや、正則化項をいつまで追加するかはハイパーパラメーターとなりますが、これらは極めて頑健なパラメーターとなっています。
- early exaggeration
early exaggeration は、学習初期に $p_{ij}$ に適当な数字を掛けるテクニックです。
これにより、$q_{ij}$ は $p_{ij}$ に対応して大きく動くようになり、学習が促進されます。その結果、まとまったクラスタが離れてマップされるため、データの大域的な構造を探索しやすくなります。
論文内の実験では、学習の最初の50ラウンドは $p_{ij}$ に4を掛けるという操作を行っています。
大規模データへの適用
t-SNE の時間計算量・空間計算量は、データ数の二乗に比例するため、1万点を超えるデータに対して適用するのは難しくなってしまいます。
しかし、ランダムサンプルしたデータに対してそのまま t-SNE を適用するだけでは、内在する多様体の構造を見失ってしまう危険性があります。例えば下図のようなデータから A, B, C の3点がサンプルされた場合、 A と B が同一クラスタに属し、かつ C は別のクラスタに属するという情報が見えなくなってしまいます。

そこで、ランダムサンプルされたデータ点 $i, j$ 間の近さ $p_{j \mid i}$ を適切に定義することで、可視化を改善しましょう。
各 landmark point (ランダムサンプルされたデータ点) について、別の landmark point に到達したら終わり、という random walk を考えます。この random walk では、ノード $\boldsymbol{x}_i$ からノード $\boldsymbol{x}_j$ に遷移する確率は $e^{-\|\boldsymbol{x}_i - \boldsymbol{x}_j\|^2}$ に比例します。
これを、全データについて作成した $k$-近傍グラフについて実行し、点 $\boldsymbol{x}_i$ から出発した中で点 $\boldsymbol{x}_j$ に到達したものの割合を $p_{j \mid i}$ とします。
こうして得られた $p_{j \mid i}$ を使用して t-SNE を実行することで、うまく全データの情報を利用して次元削減をすることができます。
random walk のシミュレーションは1秒間に100万回以上実行できる上、経験的に非常にうまくいきます。実際に、ある点 $\boldsymbol{x}_i$ から点 $\boldsymbol{x}_j$ に到達する確率を解析的に解いたものと比べても、大きな違いはありませんでした。
landmark point が非常にスパースな場合は解析的手法が適していますが、その他の場合はシミュレーションを実行することで、計算コストを削減できます。
t-SNE の弱点
t-SNE はよい可視化ができる一方で、3つの弱点があります。
1. 可視化以外の目的での次元削減においてどのように振る舞うかがわからない
t-SNE は可視化のための次元削減手法であって、一般の次元削減での振る舞いを考慮していません。
例えば3以上の次元への次元削減では、Student-t 分布の裾の部分が確率質量の多くを占めるようになるため、局所的な構造を保持することが難しくなってしまいます。そのため、Student-t 分布の自由度を1より大きくして、裾の部分の確率密度を軽くしてやるほうがよいかもしれません。
2. 次元の呪いに弱い
t-SNE はどちらかというとデータの局所的な構造を重視した次元削減を行うため、次元の呪いの影響を受けやすくなってしまっています。
本質的な次元が高く、サンプルによって内在する多様体が大きく変化してしまうようなデータの場合は、t-SNE がユークリッド距離を採用することで暗黙的に置いている、局所的な線形性の仮定が崩れてしまいまうため、うまく動作しない可能性があります。
対応策としては、元のデータから Auto Encoder などのモデルを用いて得られたデータ表現に、さらに t-SNE を適用することが考えられます。 Auto Encoder は、局所構造よりもデータに内在する多様体構造の抽出に優れた方法なので、可視化結果を改善できる可能性があります。
ただし、そのような高次元のデータを 2 ~ 3 次元で表現することはそもそも不可能であることに注意してください。
3. 大域的最適解への収束が保証されない
t-SNE は、その他の次元削減手法と違って、コスト関数が凸ではありません。そのため、最適化のパラメーターや初期値によって結果が変化してしまいます。
ただし、それらの結果の質は大きく変わるわけではないため、t-SNE の利用自体を否定するものではないと言えます。
appendix
SNE の勾配の導出
SNE の各点の勾配は、以下のように表すことができます。
\frac{\partial C}{\partial \boldsymbol{y}_{i}}=2 \sum_{j}\left(p_{j \mid i}-q_{j \mid i}+p_{i \mid j}-q_{i \mid j}\right)\left(\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right)
これを導出します。
式 $(1), (3)$ から、圧縮後の近さに関して
q_{j \mid i}=\frac{\exp \left(-\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)}{\sum_{k \neq i} \exp \left(-\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{k}\right\|^{2}\right)}
ここで、 $E_{ij} = \exp \left(-\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)$ とおいて、
q_{j \mid i} = \frac{E_{ij}}{\sum_{k \neq i} E_{ik}}
と書くことにします。
このとき、コスト関数は式 $(4)$ から、
\begin{align}
C &= \sum_k \sum_l p_{l \mid k} \log \frac{p_{l \mid k}}{q_{l \mid k}} \\
&= \sum_k \sum_l p_{l \mid k} \left( \log p_{l \mid k} - \log \frac{E_{kl}}{\sum_{m \neq k} E_{km}} \right) \\
&= \sum_k \sum_l p_{l \mid k} \log p_{l \mid k} - \sum_k \sum_l p_{l \mid k} \log E_{kl} + \sum_k \sum_l p_{l \mid k} \log {\sum_{m \neq k} E_{km}}
\end{align}
これを $\boldsymbol{y}_i$ について微分していきます。第一項は $\boldsymbol{y}_i$ に依存しないため、無視することができます。
第二項は、 $i$ に関する部分のみ抜き出して
- \frac{\partial}{\partial \boldsymbol{y}_i} \sum_k \sum_l p_{l \mid k} \log E_{kl} = - \sum_l p_{l \mid i} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{il} - \sum_k p_{i \mid k} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{ki}
ここで、
\frac{\partial}{\partial \boldsymbol{y}_i} E_{ij} = -2 \left(\boldsymbol{y}_i - \boldsymbol{y}_j \right) E_{ij}
\begin{align}
\frac{\partial}{\partial \boldsymbol{y}_i} \log E_{ij} &= \frac{1}{E_{ij}} \frac{\partial}{\partial \boldsymbol{y}_i} E_{ij} \\
&= -2 \left(\boldsymbol{y}_i - \boldsymbol{y}_j \right)
\end{align}
であり、かつ定義より $E_{ij} = E_{ji}$ なので、
- \sum_l p_{l \mid i} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{il} - \sum_k p_{i \mid k} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{ki} = 2 \sum_k \left(\boldsymbol{y}_i - \boldsymbol{y}_k \right) \left( p_{k \mid i} + p_{i \mid k} \right)
となります。このとき $l$ を $k$ で置き換えています。
第三項は、 $l$ について和をとることができて、
\begin{align}
\frac{\partial}{\partial \boldsymbol{y}_i} \sum_k \sum_l p_{l \mid k} \log {\sum_{m \neq k} E_{km}} &= \frac{\partial}{\partial \boldsymbol{y}_i} \sum_k \log {\sum_{m \neq k} E_{km}} \\
&= \sum_k \frac{1}{\sum_{m \neq k} E_{km}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m \neq k} E_{km} \\
&= \sum_k \frac{1}{\sum_{m \neq k} E_{km}} \frac{\partial}{\partial \boldsymbol{y}_i} E_{ki} + \frac{1}{\sum_{m \neq i} E_{im}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m \neq i} E_{im}
\end{align}
ここで、 $\frac{\partial}{\partial \boldsymbol{y}_i} E_{ii} = 0$ より、上式の第二項は
\begin{align}
\frac{1}{\sum_{m \neq i} E_{im}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m \neq i} E_{im} &= \frac{1}{\sum_{m \neq i} E_{im}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m} E_{im} \\
&= \sum_{k} \frac{1}{\sum_{m \neq i} E_{im}} \frac{\partial}{\partial \boldsymbol{y}_i} E_{ik}
\end{align}
と書けます。2番目の等式では、2つ目の $m$ を $k$ で置き換えています。
よって、
\begin{align}
\sum_k \frac{1}{\sum_{m \neq k} E_{km}} \frac{\partial}{\partial \boldsymbol{y}_i} E_{ki} + \frac{1}{\sum_{m \neq i} E_{im}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m \neq i} E_{i} &= -2 \sum_k \left( \boldsymbol{y}_i - \boldsymbol{y}_k \right) \left( \frac{E_{ki}}{\sum_{m \neq k} E_{km}} + \frac{E_{ik}}{\sum_{m \neq i} E_{im}} \right) \\
&= -2 \sum_k \left( \boldsymbol{y}_i - \boldsymbol{y}_k \right) \left( q_{i \mid k} + q_{k \mid i} \right)
\end{align}
以上より、
\begin{align}
\frac{\partial C}{\partial \boldsymbol{y}_i} &= 2 \sum_k \left(\boldsymbol{y}_i - \boldsymbol{y}_k \right) \left( p_{k \mid i} + p_{i \mid k} \right) - 2 \sum_k \left( \boldsymbol{y}_i - \boldsymbol{y}_k \right) \left( q_{i \mid k} + q_{k \mid i} \right) \\
&= 2 \sum_{j}\left(p_{j \mid i}-q_{j \mid i}+p_{i \mid j}-q_{i \mid j}\right)\left(\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right)
\end{align}
が導出できます。
t-SNE の勾配の導出
t-SNE の各点の勾配は、以下のように表すことができます。
\frac{\partial C}{\partial \boldsymbol{y}_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right)\left(1+\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)^{-1}
これを導出します。
式 $(6)$ から、
q_{i j}=\frac{\left(1+\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)^{-1}}{\sum_{k, l \neq k}\left(1+\left\|\boldsymbol{y}_{k}-\boldsymbol{y}_{l}\right\|^{2}\right)^{-1}}
ここで、 $E_{ij} = 1+\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}$ とおいて、
q_{ij} = \frac{E_{ij}^{-1}}{\sum_{k, l \neq k} E_{kl}^{-1}}
と書くことにします。
このとき、コスト関数は式 $(5)$ から、
\begin{align}
C &= \sum_k \sum_l p_{kl} \log \frac{p_{kl}}{q_{kl}} \\
&= \sum_k \sum_l p_{kl} \left( \log p_{kl} - \log \frac{E_{kl}^{-1}}{\sum_{m, n \neq m} E_{mn}^{-1}} \right) \\
&= \sum_k \sum_l p_{kl} \log p_{kl} - \sum_k \sum_l p_{kl} \log E_{kl}^{-1} + \sum_k \sum_l p_{kl} \log \sum_{m, n \neq m} E_{mn}^{-1}
\end{align}
これを $\boldsymbol{y}_i$ について微分していきます。第一項は $\boldsymbol{y}_i$ に依存しないため、無視することができます。
第二項は、 $i$ に関する部分のみ抜き出して
- \frac{\partial}{\partial \boldsymbol{y}_i} \sum_k \sum_l p_{kl} \log E_{kl}^{-1} = - \sum_l p_{il} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{il}^{-1} - \sum_k p_{ki} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{ki}^{-1}
ここで、
\frac{\partial E_{ij}}{\partial \boldsymbol{y}_i} = 2 \left( \boldsymbol{y}_i - \boldsymbol{y}_j \right)
\begin{align}
\frac{\partial \log E_{ij}^{-1}}{\partial \boldsymbol{y}_i} &= - \frac{1}{E_{ij}} \frac{\partial E_{ij}}{\partial \boldsymbol{y}_i} \\
&= - \frac{2}{E_{ij}} \left( \boldsymbol{y}_i - \boldsymbol{y}_j \right)
\end{align}
であり、かつ定義より $E_{ij} = E_{ji}, p_{ij} = p_{ji}$ なので、
- \sum_l p_{il} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{il}^{-1} - \sum_k p_{ki} \frac{\partial}{\partial \boldsymbol{y}_i} \log E_{ki}^{-1} = 4 \sum_k \frac{p_{ik}}{E_{ik}} \left( \boldsymbol{y}_i - \boldsymbol{y}_k \right)
となります。このとき $l$ を $k$ で置き換えています。
第三項は、 $k$ と $l$ について和をとることができて、
\begin{align}
\frac{\partial}{\partial \boldsymbol{y}_i} \sum_k \sum_l p_{kl} \log \sum_{m, n \neq m} E_{mn}^{-1} &= \frac{\partial}{\partial \boldsymbol{y}_i} \log \sum_{m, n \neq m} E_{mn}^{-1} \\
&= \frac{1}{\sum_{m, n \neq m} E_{mn}^{-1}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m, n \neq m} E_{mn}^{-1} \\
&= \frac{1}{\sum_{m, n \neq m} E_{mn}^{-1}} \left( \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{m} E_{mi}^{-1} + \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{n \neq i} E_{in}^{-1} \right) \\
&= \frac{2}{\sum_{m, n \neq m} E_{mn}^{-1}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{k} E_{ik}^{-1}
\end{align}
ここで、
\frac{\partial E_{ij}^{-1}}{\partial \boldsymbol{y}_i} = - 2 E_{ij}^{-2} \left( \boldsymbol{y}_i - \boldsymbol{y}_j \right)
より、
\begin{align}
\frac{2}{\sum_{m, n \neq m} E_{mn}^{-1}} \frac{\partial}{\partial \boldsymbol{y}_i} \sum_{k} E_{ik}^{-1} &= -4 \sum_k \frac{E_{ik}^{-1}}{\sum_{m, n \neq m} E_{mn}^{-1}} E_{ik}^{-1} \left( \boldsymbol{y}_i - \boldsymbol{y}_j \right) \\
&= -4 \sum_k \frac{q_{ik}}{E_{ik}} \left( \boldsymbol{y}_i - \boldsymbol{y}_j \right)
\end{align}
となります。
以上より、
\frac{\partial C}{\partial \boldsymbol{y}_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right)\left(1+\left\|\boldsymbol{y}_{i}-\boldsymbol{y}_{j}\right\|^{2}\right)^{-1}
が導出できます。