コインを投げたときに表が出る割合を知りたいとします。おそらく半々ぐらいの割合で表と裏が出るだろうと思われますが、表が出やすい可能性や、裏が出やすい可能性もあります。現時点ではまだ一度も投げてみていないので、なんとも言えない状況です。
さて、このコインを5回投げてみたところ4回表が出たので、「もしかしたら表が出やすいコインなのでは?」と思いはじめました。ただし、まだ5回分のデータしかないので偶然そうなっただけかも知れません。
さらに続けて100回投げてみたところ表が出たのは76回だったので、「このコインは表が出やすい」というより強い確信を持ちました。
このように、コイン投げの結果という「データ」が多く集まるほど、表が出る割合についての「確信度合い」が強まっていくわけですが、ベイズ統計学では「確信度合い」を確率として数値に置き換えて考えます。そして、得られたデータから「確信度合い」を計算しようというのが、ベイズ推定になります。
事前確率をおく
もう少し具体的に考えてみます。表が出る割合を$\theta$としたとき、$\theta=0.5$(表と裏が半々)、$\theta=0.8$(表が出やすい)・・・など、$\theta$の値について様々な説を考えます。
ここで、コイン投げをする前の時点で、$\theta=0.5$などのそれぞれの説がどの程度信用できると考えているかを、たとえば次のように確率として表現します。
| 表が出る割合$\theta$についての説 | 確率 |
|---|---|
| $\theta=0$ | 0.01 |
| $\theta=0.1$ | 0.07 |
| $\theta=0.2$ | 0.10 |
| $\theta=0.3$ | 0.12 |
| $\theta=0.4$ | 0.13 |
| $\theta=0.5$ | 0.14 |
| $\theta=0.6$ | 0.13 |
| $\theta=0.7$ | 0.12 |
| $\theta=0.8$ | 0.10 |
| $\theta=0.9$ | 0.07 |
| $\theta=1$ | 0.01 |
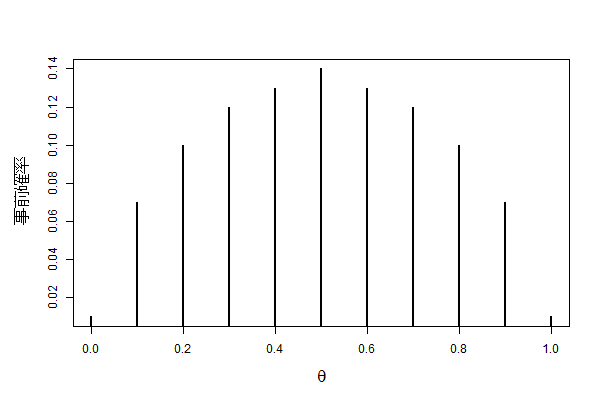
これをグラフに描いたのが下図になります。$\theta=0.5$あたりの確率が頂点になっており、「たぶん表と裏が半分ずつぐらい出るんじゃないかな」という心理を表現したものになっています。このようにコイン投げをする前の時点での$\theta$の確率を、事前確率と呼びます。
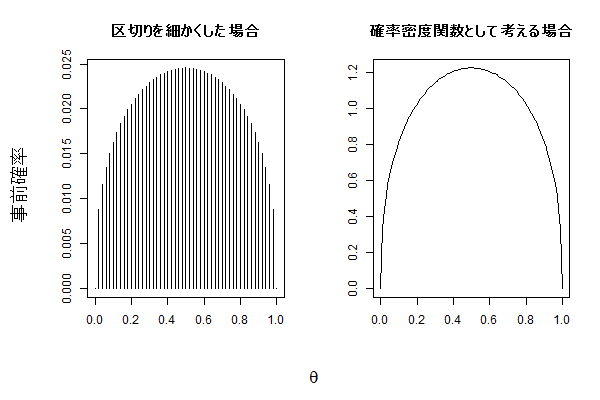
なお$\theta$については上の表に記載した値だけでなく、$\theta=0.55$などもっと多くの説を考えることができます。理論上は、$\theta=0$(必ず裏が出る)から$\theta=1$(必ず表が出る)の間で無限個の説を考えることができ、その場合は下図のように事前確率を何らかの確率密度関数として考えることになりますが、今回はわかりやすさ重視で$\theta$は上の表の値しかとらないことにします。
事後確率を計算する
次に、「5回中4回表が出た」というデータが得られたので、これをベイズの定理を用いて$\theta$の確率に反映させることにします。ベイズの定理は、次のようなシンプルな数式で表されます。
$$
事後確率 \propto 尤度 \times 事前確率
$$
「事後確率は、尤度と事前確率を掛け算した値に比例する」と読みます。事後確率とは「5回中4回表」というデータが得られた後の時点での$\theta$の確率、尤度とはたとえば$\theta=0.5$という説を仮定したときに「5回中4回表」というデータが得られる確率を意味します。
実際に事後確率を計算してみましょう。
# θのとりうる値
theta <- seq(0, 1, 0.1)
# 事前分布
prior <- c(0.01, 0.07, 0.1, 0.12, 0.13, 0.14, 0.13, 0.12, 0.1, 0.07, 0.01)
# データ(5回中4回表が出た)
data <- list(n = 5, s = 4)
# 尤度
likelihood <- dbinom(data$s, size = data$n, prob = theta)
# 事後分布
posterior <- likelihood * prior
posterior <- posterior / sum(posterior) # 合計が1になるようにsum(posterior)で割る
print(sprintf("%.2f", posterior))
# [1] "0.00" "0.00" "0.00" "0.02" "0.06" "0.12" "0.19" "0.24" "0.23" "0.13" "0.00"
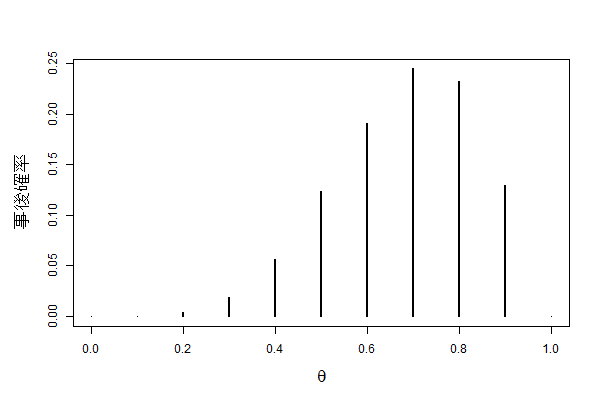
事後確率は、事前確率に比べて右に傾いたヒストグラムになっています。「もしかしたら表が出やすいんじゃない?」という心理を表現できています。
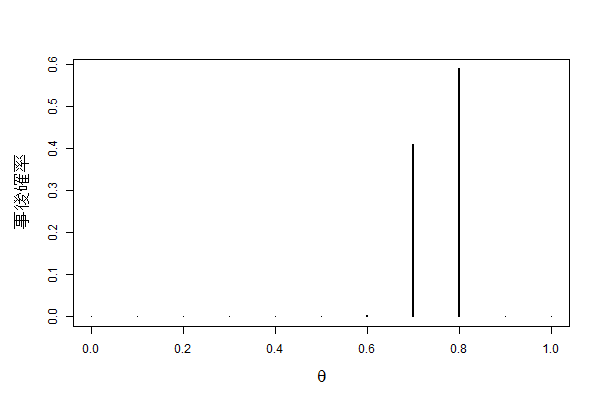
「さらに100回投げて76回表が出た」というデータを反映するには、現在の事後分布を事前分布にして同じ手順で計算します。すると、ほぼ間違いなく$\theta=0.7もしくは0.8$という結果になりました。
まとめ
このようにベイズ推定は、事前に考えている仮説にデータを加えることで確信が強くなっていく様子を確率で計算します。ベイズ推定の結果である事後確率は常に、ヒストグラムや曲線で表現されるような確率分布であるというをとりあえずイメージできればいいかと思います。