はじめに
YouTubeを見ていたらこんな動画が目に入りました。
【大決戦】コンピュータを使ってでもパズル王に勝ちたい！！
動画の内容は、以下の問題を解くのを人間vs.プログラミングで対決するというものです。
【問題】
数個の数字が与えられるので、指定された数字が計算できる式を答えよ(使えるのは四則演算のみ)
動画を見ながら、自分だったらどう解くかを考えたので実際にコーディングしてみました。
どのような問題なのか？
まずは問題を細かく整理していきましょう。
問題の内容
例を出すと「1, 2, 3, 4 から 11 を作れ」みたいな問題となります。この問題の場合、1 × 3 + 4 × 2 = 11 みたいな式が成り立つので、これが解答の一例となります。
答えが複数ある場合もあります( 3 × 4 - 2 + 1 も 11 になります)。複数の解がある場合、いずれかの数式を答えられれば正解となります。
制約の整理
プログラムを書く前に、入力として与えられるデータの大きさや個数を整理しておきます。
競技プログラミング(競プロ)だと制約と言われています。
競プロのコンテストでは、この制約をもとに高速に処理できるアルゴリズムを考え、実装していきます。
動画に出てきた問題をもとに整理した制約は以下のとおりです。
- 「 $a_1, a_2, ...$ から$B$を作れ」の問題の $a_1, a_2, ...$ の値は1〜9の数字で個数は4〜6個
- $B$の値は1桁もしくは2桁の数字
- 動画では公言していないけど、解が存在する問題(のはず、、、)
競プロのように書くとこんな感じになります。
【問題】
$A = (a_1, a_2, ..., a_k)$ という $k$ 個の整数と整数 $B$ が与えられる。
$A$ の数字と四則演算(+-×÷)により演算結果が $B$ となる数式を文字列として出力せよ。
答えが複数ある場合は、いずれか1つ出力すれば良い。
なお、必ず解答が存在することが保障されている。
【制約事項】
- 入力はすべて整数
- $4 ≤ k ≤ 6$
- $1 ≤ a_i ≤ 9$
- $1 ≤ B < 100$
この問題を解くアルゴリズムを考えていきます。
アルゴリズム検討&実装
以降から、実際に問題を解くプログラムについて考えていきます。
概要
動画の問題の場合、与えられる数字はせいぜい7個なので、作れる数式を全て試す方針(全探索と呼ばれたします)で考えます。数式を全探索する際、日頃私たちが使っている式の形だと四則演算の計算順序(乗算/除算が先、括弧内の計算が先など)を考える必要があります。計算順序を考えつつ全探索するのは大変なので、楽をするために逆ポーランド記法というものを使います。
この逆ポーランド記法と深さ優先探索(DFS)により、数式を全探索することができます。後はそれらの数式を実際に計算し、作りたい数字ができる数式をどれか一つ答えれば良いです。
逆ポーランド記法
数式やプログラムの記法の一種です。通常の数式と比べて、演算子(+-×÷)と非演算子(数字)の並び順が特殊な書き方となります。
例えば、3+4の数式を逆ポーランド記法で書くと、34+となります。
(3+4)×(1-2)の数式は、34+12-×となります。
逆ポーランド記法はあまり見慣れないと思いますが、応用情報の試験で出てきたりします。知っておいても損はないでしょう。
詳細は以下のWikiやネットで調べてみてください。
逆ポーランド記法(Wiki)
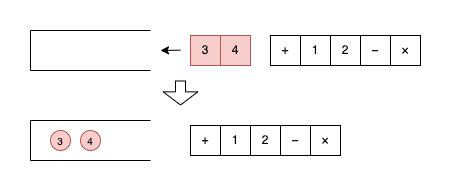
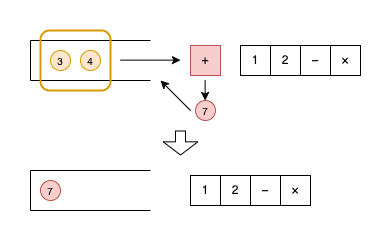
実際に演算する際は、左から順に見ていき、以下のように処理することで計算できます。
-
非演算子(数字)の場合は、値を保存する。
-
演算子(+-×÷)の場合は、手順1で保存した値のうち最新のものを2つ取り出して演算します。そして演算結果を保存する。
処理が終わると数字が1つだけ残り、それが最終的な演算結果となります(俗にいうFILOの動きとなります)。手順2以降の処理は以下の通りで、最終的な結果は「-7」となります。
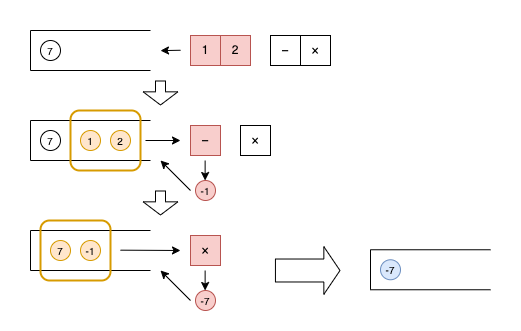
この実装は、スタック(pythonだとリスト)を使うことで簡単に実装できます。
# 有理数の計算をサポートするライブラリ
# 計算結果が分数になった際、除算による計算誤差が発生してしまうため、このライブラリを使用して対応します。
# 詳細は下記リンクを確認してください。
# https://docs.python.org/ja/3/library/fractions.html
from fractions import Fraction
# rpnには、「34+」や「34+12-*」などの文字列を与える
def calc_RPN_simple(rpn):
def ope(a, b, op):
match op:
case "+": return a + b
case "-": return a - b
case "*": return a * b
case "/": return a / b
ops = "+-*/"
stack = []
for i, c in enumerate(rpn):
# 数値(演算子ではない)の場合、スタックに格納
if c not in ops:
stack.append(Fraction(int(c), 1))
# 演算子の場合は、スタックから数値を2つ取り出して演算する
else:
var1 = stack.pop()
var2 = stack.pop()
# 計算を実施し、結果をスタックに格納
result = ope(var2, var1, c)
stack.append(result)
# 計算結果を返却
return stack[0]
ベースは上のコードで問題ないのですが、今回は以下3点を対応する必要があります。
① 不正な逆ポーランド記法の場合、エラーとなる（例えば「345+」みたいに数字が多すぎたり、「34+*」みたいに演算子が多すぎたり等）
② ゼロ割が発生する可能性があるため対策する必要がある
③ 今回のクイズでは演算結果ではなく、数式を答える必要があるため、数式を返すような処理が必要になる
①〜③を追加したコードは下記のようになります。
from fractions import Fraction
# ➂ return_formulaによって、演算結果を返すか、数式を返すかを切り替えられる
def calc_RPN(rpn, return_formula=False):
def ope(a, b, op):
match op:
case "+": return a + b
case "-": return a - b
case "*": return a * b
case "/": return a / b if b != 0 else float("INF") # ➁ ゼロ除算が発生した場合は、無限(INF)とする
case _:
# +-*/以外の記号の場合は例外を出す
raise ValueError(f"op(char) is invalid value (value: {op})")
ops = "+-*/"
stack = []
for i, c in enumerate(rpn):
# 数値(演算子ではない)の場合、スタックに格納
if c not in ops:
stack.append(Fraction(int(c), 1))
# 演算子の場合は、スタックから数値を2つ取り出して演算する
else:
# ➀ 演算子に対して、数値が不足している場合は例外を出す
if len(stack) < 2:
raise ValueError(f"There is an error in reverse polish notation (notation: {rpn}, index: {i}, char: {c})")
var1 = stack.pop()
var2 = stack.pop()
# ➂ 数式を返却する場合は、演算はせずに演算式をスタックに格納していく
if return_formula:
result = f"{var2} {c} {var1}"
if i < len(rpn) - 1:
result = f"({result})"
stack.append(result)
# 計算結果を返却する場合は、演算結果をスタックに格納
else:
result = ope(var2, var1, c)
# ➁ ゼロ割が発生して演算結果が無限(INF)になった場合は、その時点で処理を終了し、無限(INF)を返却する
if result == float("inf"):
return float("inf")
stack.append(result)
# ➀ 数値に対して、演算子が不足している場合は例外を出す
if len(stack) > 1:
raise ValueError("Insufficient number of operators in reverse polish notation")
# ➂ 計算結果 もしくは 数式を返却
return stack[0] if return_formula else str(stack[0])
実際に動かしてみた結果が以下となります。
from calc_rpn import calc_RPN
print(f"{calc_RPN('12+')} = {calc_RPN('12+', return_formula=True)}")
print(f"{calc_RPN('34+12-*')} = {calc_RPN('34+12-*', return_formula=True)}")
"""
動作結果
> 3 = 1 + 2
> -7 = (3 + 4) * (1 - 2)
"""
構文エラー対策や例外処理を入れるとコード量が増えますが、逆ポーランド記法自体の計算処理は簡単に実装できます。
でも何故この記法を使うのでしょう？実はこの後の全探索の際に実装がとても楽になるのです。
深さ優先探索(DFS)による全探索
逆ポーランド記法だと括弧を書かなくても演算の優先順位を考えることができます。また、全探索する上でとても都合が良いです。
与えられた数字に対して以下の処理を行うことで全探索ができます。
- スタック数が2つ未満の場合、与えられた数字から一つ選択し、スタック数を1だけ加算する(2つ未満の時に演算子を選択してしまうと、計算できない式となってしまいます)。
- スタック数が2つ以上の場合、与えられた数字もしくは演算子(+-×÷)から一つ選択する。選択した値が数字の場合はスタックを1だけ加算し、演算子の場合は1だけ減算する。
- 全ての数字に対して処理が終わったら、選択した値を文字として選択した順番にくっつける。
- 1から3の処理を全てのパターンで実施する。
また処理を行う際には、以下の点には気をつけます。
演算子の個数は、与えられた数字の個数-1だけになります。多くても少なくてもダメです。(数式を書いた時、数字の間に演算子が入るのでイメージしやすいと思います)
上記の処理は言葉にして表現すると分かりにくいですが、木構造で図示すると理解しやすいと思います。木構造で説明すると以下のようになります。
入力の数字が「1、2、2」の時を例として考えてみます。
-
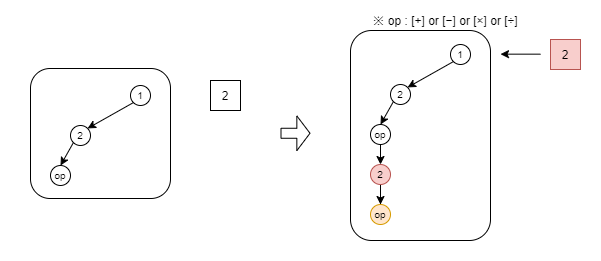
スタック数が2つ未満(ここでは木の深さが2未満)の場合、現在見ている数字(赤四角)を深く伸びていくようにノードとして追加していきます。最初は何もないので➀のノードを追加します。次に、➀の下に➁のノードを追加します。
-
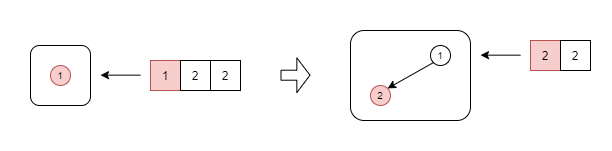
スタック数が2つ以上(ここでは木の深さが2以上)の場合、「現在見ている数字」もしくは「演算子(+-×÷)」をノードとして追加します。便宜上、演算子を「op」と記載していますが、[+] [-] [×] [÷] のすべてを三択する必要があります。(opのノードの個所に、[+] [-] [×] [÷] が横に並ぶような木構造になります)。
-
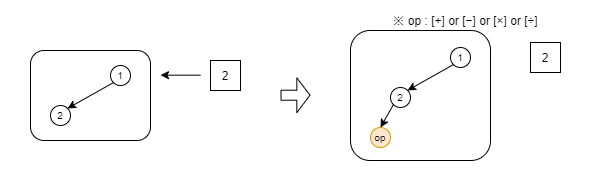
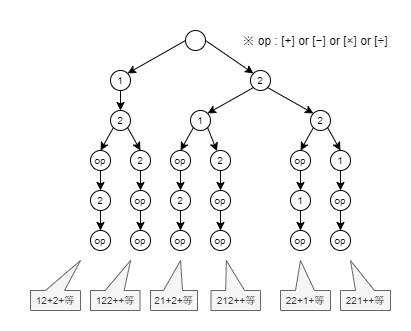
引き続き、「現在見ている数字」もしくは「演算子(+-×÷)」をノードとして追加していきます。なお、演算子の個数は「<与えられた数字> - 1」の個数だけになることに注意します。深さが最大（数字の個数＋演算子の個数）となったら、一番下のノードから頂点のノードを結ぶ数字と演算子を文字としたものが、逆ポーランド記法となります。
※下記の図だと「op」が [+] の場合、「12+2+」が逆ポーランド記法
-
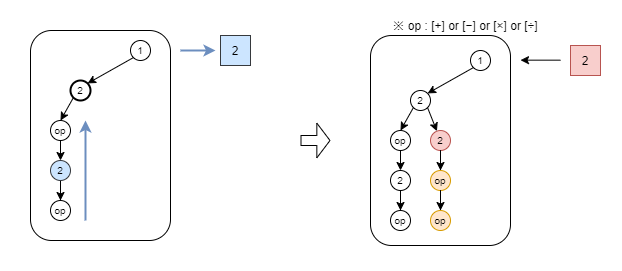
深さが最大まで探索したら、一番下のノードから最も近くかつ分岐が存在するノード(太文字の➁)まで戻ります。戻る際は経路上に存在する数字は探索対象（青四角）として戻します。戻ったノードから、手順2から再度実施していきます。
-
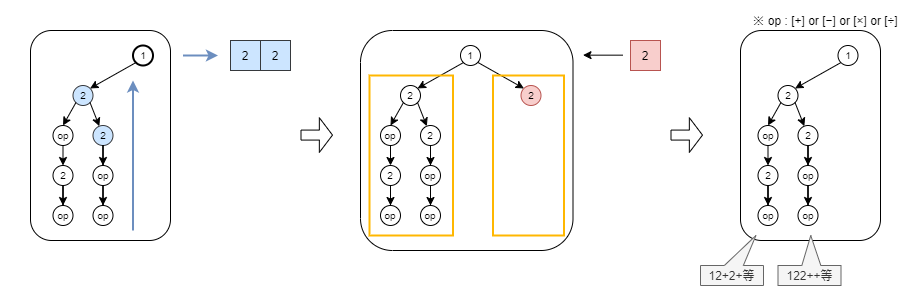
一通り探索出来たら一番上のノードまで戻り、手順1から再度実施していきます。ただ今回の場合、頂点から延びるノードは両方とも➁となります。同じ数字が横に並ぶ際は、その木構造(左右の黄色四角)は同じ形になります。同じ形の木構造からは逆ポーランド記法を列挙すると重複してしまうため、同じ階層に同じ数字が出てきた際は、探索をスキップします。
※最終的には、下記の図の右側の木構造となります。
-
手順5までは➀を頂点とした場合の木構造であり、他の数字を頂点としたときの木構造も洗い出す必要があります(今回の場合は➁も頂点にして考える必要がある)。➀の頂点まで遡り、遡る際は経路上に存在する数字は探索対象（青四角）として戻します。そして、探索対象の数字を一つ右(1 → 2)に移して再度木構造を作っていきます。
-
すべての手順を実施し終えると、以下のような木構造となります。
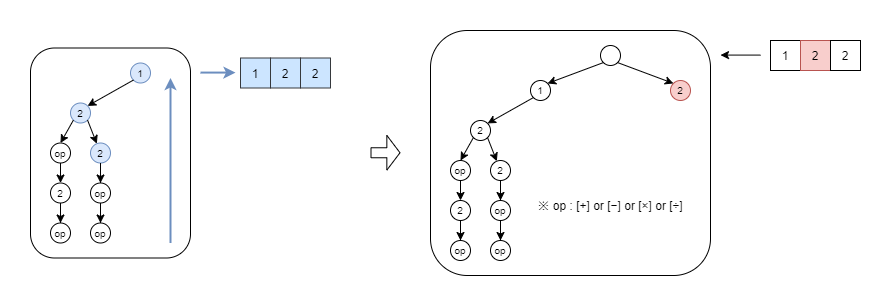
「1、2、2」の入力値から木構造を作ると、深さが最大となるノードは6つとなりました。ただ、「op」は [+] [-] [×] [÷] の4つが入ることになります。そして、各逆ポーランド記法には「op」が2つあるため、6×4×4=96パターンを全列挙する結果となっています。
このようにして、深さ優先探索(DFS)により全探索を行うことができます。
コードは以下のようになります。
def search_RPN_all(input_nums):
n_nums = len(input_nums) # 入力数値の個数
n_ops = n_nums - 1 # 演算子の個数
n_rpn = n_nums + n_ops # 逆ポーランド記法の文字数
used = [False] * n_nums # 使用したinput_numsを記憶する変数
rpns = [] # 生成した逆ポーランド記法を保存する変数
# DFSにより、あり得る逆ポーランド記法を探索
# rpn: 作成中の逆ポーランド記法
# n_stack: スタックしている数値の個数
def dfs(rpn="", n_stack=0):
nonlocal rpns, used
# 逆ポーランド記法を生成できたらいったん表示する
if len(rpn) >= n_rpn:
print(rpn, end=", ")
return
appeared = set() # 重複防止のために、出現した数値を保存する変数
for i, num in enumerate(input_nums):
# 未使用 かつ 未出現の数値の場合、追加可能
if (not used[i]) and (num not in appeared):
appeared.add(num)
used[i] = True
dfs(rpn + str(num), n_stack + 1)
used[i] = False
# スタックが2つ以上ある場合は演算子が追加可能
if n_stack >= 2:
for op in "+-*/":
dfs(rpn + op, n_stack - 1)
dfs()
return rpns
実際に動かしてみた結果が以下となります。
from search_rpn_all import search_RPN_all
search_RPN_all([1, 2])
print("\n" + "-"*20)
search_RPN_all([1, 1])
print("\n" + "-"*20)
search_RPN_all([1, 2, 3])
"""
動作結果
> 12+, 12-, 12*, 12/, 21+, 21-, 21*, 21/,
> --------------------
> 11+, 11-, 11*, 11/,
> --------------------
> 123++, 123+-, 123+*, 123+/, 123-+, 123--, 123-*, 123-/, 123*+, 123*-, 123**, 123*/, 123/+, 123/-, 123/*, 123//, 12+3+, 12+3-, 12+3*, 12+3/, 12-3+, 12-3-, 12-3*, 12-3/, 12*3+, 12*3-, 12*3*, 12*3/, 12/3+, 12/3-, 12/3*, 12/3/, 132++, 132+-, 132+*, 132+/, 132-+, 132--, 132-*, 132-/, 132*+, 132*-, 132**, 132*/, 132/+, 132/-, 132/*, 132//, 13+2+, 13+2-, 13+2*, 13+2/, 13-2+, 13-2-, 13-2*, 13-2/, 13*2+, 13*2-, 13*2*, 13*2/, 13/2+, 13/2-, 13/2*, 13/2/, 213++, 213+-, 213+*, 213+/, 213-+, 213--, 213-*, 213-/, 213*+, 213*-, 213**, 213*/, 213/+, 213/-, 213/*, 213//, 21+3+, 21+3-, 21+3*, 21+3/, 21-3+, 21-3-, 21-3*, 21-3/, 21*3+, 21*3-, 21*3*, 21*3/, 21/3+, 21/3-, 21/3*, 21/3/,
231++, 231+-, 231+*, 231+/, 231-+, 231--, 231-*, 231-/, 231*+, 231*-, 231**, 231*/, 231/+, 231/-, 231/*, 231//, 23+1+, 23+1-, 23+1*, 23+1/, 23-1+, 23-1-, 23-1*, 23-1/, 23*1+, 23*1-, 23*1*, 23*1/, 23/1+, 23/1-, 23/1*, 23/1/, 312++, 312+-, 312+*, 312+/, 312-+, 312--, 312-*, 312-/, 312*+, 312*-, 312**, 312*/, 312/+, 312/-, 312/*, 312//, 31+2+, 31+2-, 31+2*, 31+2/, 31-2+, 31-2-, 31-2*, 31-2/, 31*2+, 31*2-, 31*2*, 31*2/, 31/2+, 31/2-, 31/2*, 31/2/, 321++, 321+-, 321+*, 321+/, 321-+, 321--, 321-*, 321-/, 321*+, 321*-, 321**, 321*/, 321/+, 321/-, 321/*, 321//, 32+1+, 32+1-, 32+1*, 32+1/, 32-1+, 32-1-, 32-1*, 32-1/, 32*1+, 32*1-, 32*1*, 32*1/, 32/1+, 32/1-, 32/1*, 32/1/,
"""
実際に問題を解くコードの実装
先ほどの全探索のコードでは、作成した逆ポーランド記法を表示するだけでした。ただ、今回行いたいことは「作成した逆ポーランド記法を計算した結果、指定した数字が作れるかどうか」になります。そのため、以下の3箇所のコードを見直す必要があります。
➀search_RPN_all関数の引数に「指定した数字」を追加
➁search_RPN_all関数の「生成した逆ポーランド記法の表示」の処理を「生成した逆ポーランド記法の計算結果と指定した数字が一致していた場合、数式を返却する」処理に置き換え
➂search_RPN_all関数の中にあるDFS関数で正解となる数式が見つからない場合、Noneを返却する処理を追加
➀から➂の見直しをすることで、指定した数字が答えとなる数式、もしくはNone (解無しの場合)を返却する処理に変換することができます。
置き換え後のコードは以下のようになります。(置き換え後の関数名をsolverとします)
# /// 変更箇所➀：引数にcreate_numを追加 ///
def solver(input_nums, create_num):
n_nums = len(input_nums) # 入力数値の個数
n_ops = n_nums - 1 # 演算子の個数
n_rpn = n_nums + n_ops # 逆ポーランド記法の文字数
used = [False] * n_nums # 使用したinput_numsを記憶する変数
# DFSにより、あり得る逆ポーランド記法を探索し、create_numと一致する式の場合は、その式(文字列)を返却する
# rpn: 作成中の逆ポーランド記法
# n_stack: スタックしている数値の個数
def dfs(rpn="", n_stack=0):
nonlocal used
# /// 変更箇所➁：表示処理から一致確認処理に置き換え ///
if len(rpn) >= n_rpn:
# 生成した逆ポーランド記法の計算を実施
# create_numと一致した式(文字列)を返却し、一致しない場合はNoneを返却
if (calc_RPN(rpn) == str(create_num)):
return calc_RPN(rpn, return_formula=True)
else:
return None
appeared = set() # 重複防止のために、出現した数値を保存する変数
for i, num in enumerate(input_nums):
# 未使用 かつ 未出現の数値の場合、追加可能
if (not used[i]) and (num not in appeared):
appeared.add(num)
used[i] = True
formula = dfs(rpn + str(num), n_stack + 1)
# 該当する式が見つかった場合は式を返却
if formula:
return formula
used[i] = False
# スタックが2つ以上ある場合は演算子が追加可能
if n_stack >= 2:
for op in "+-*/":
formula = dfs(rpn + op, n_stack - 1)
# 該当する式が見つかった場合は式を返却
if formula:
return formula
# /// 変更箇所➂：Noneの返却処理を追加 ///
# create_numと一致する式が見つからない場合はNoneを返却
return None
# /// 変更箇所 ///
# 探索を実施し、解(式)を返却
return dfs()
実際に動かしてみた結果が以下となります。
from quizknock_solver import solver
print(solver([1, 2, 3, 4], 11))
"""
動作結果
> 1 - (2 - (3 * 4))
"""
これで問題を解くコード(solver)が完成となります。
では、実際に動画で出てきた問題を解いてみます。
動画で出ている問題を実際に解いてみる
動画の中で登場した問題を解いてみます。
動画を目視で確認し、以下のように手動で問題リストを用意しました。（結構大変でした、、）
# 問題 (問題番号、入力となる数値、作成する数値)
QUERY = [
(1, [1, 2, 3, 4], 15), (2, [4, 8, 8, 9], 23), (3, [3, 5, 8, 9], 24), (4, [1, 3, 5, 7], 19), (5, [1, 2, 2, 6, 7, 9], 16),
(6, [1, 2, 3, 3, 3, 9], 13), (7, [1, 4, 5, 6, 6, 6], 9), (8, [1, 5, 6, 7], 13), (9, [1, 2, 3, 6, 6], 24), (10, [2, 3, 4, 4], 19),
(11, [2, 4, 7, 9, 9], 14), (12, [3, 4, 7, 8, 8, 9], 8), (13, [1, 3, 4, 6], 9), (14, [2, 3, 9, 9], 14), (15, [1, 3, 4, 3, 5], 22),
(16, [1, 4, 6, 6], 8), (17, [1, 1, 4, 6, 6, 8], 17), (18, [4, 4, 5, 7, 8], 16), (19, [3, 3, 4, 7], 25), (20, [2, 2, 6, 8, 9], 17),
(21, [1, 8, 9, 9], 16), (22, [2, 5, 5, 6, 6, 8], 15), (23, [2, 2, 3, 6, 8], 12), (24, [6, 6, 7, 8, 9], 22), (25, [1, 6, 8, 8], 18),
(26, [2, 5, 7, 7, 8], 18), (27, [3, 3, 4, 8], 19), (28, [5, 6, 9, 9], 8), (29, [1, 2, 3, 4, 8, 9], 22), (30, [1, 2, 7, 8], 17),
(31, [1, 1, 3, 6, 9], 14), (32, [2, 6, 7, 9], 21), (33, [1, 4, 6, 7], 23), (34, [1, 4, 4, 6, 8], 12), (35, [1, 3, 5, 9], 14),
(36, [1, 1, 3, 5, 5, 7], 24), (37, [2, 2, 5, 6], 12), (38, [1, 6, 8, 8], 18), (39, [1, 3, 4, 6], 13), (40, [2, 6, 6, 8, 8], 19),
(41, [3, 4, 4, 9], 11), (42, [1, 4, 6, 9], 17), (43, [4, 7, 8, 8], 10), (44, [1, 6, 8, 9], 18), (45, [3, 4, 6, 8], 18),
(46, [1, 2, 4, 8, 9], 13), (47, [3, 7, 8, 8], 18), (48, [1, 2, 3, 3, 6], 18), (49, [4, 5, 9, 9, 9], 17), (50, [5, 6, 7, 9], 19),
(51, [3, 6, 6, 8], 21), (52, [1, 2, 7, 7, 8], 17), (53, [2, 3, 6, 6], 19)
]
問題が用意できたら、以下のコードで全問題を解くことができます。
from sample_input import QUERY
from quizknock_solver import solver
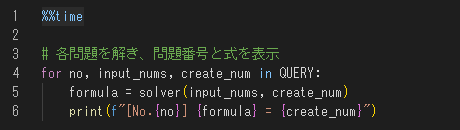
# 各問題を解き、問題番号と式を表示
for no, input_nums, create_num in QUERY:
formula = solver(input_nums, create_num)
print(f"[No.{no}] {formula} = {create_num}")
動作結果は少し長いので、トグルリストの中に記載します。
動作結果
"""
動作結果
[No.1] 1 + (2 * (3 + 4)) = 15
[No.2] (4 - (9 / 8)) * 8 = 23
[No.3] (3 * 9) + (5 - 8) = 24
[No.4] ((1 + 7) * 3) - 5 = 19
[No.5] 1 * (2 * (2 * (6 + (7 - 9)))) = 16
[No.6] 1 - (2 * (3 + (3 - (3 + 9)))) = 13
[No.7] 1 * (4 + (5 + (6 * (6 - 6)))) = 9
[No.8] 1 - ((5 - 7) * 6) = 13
[No.9] 1 * (2 / (3 / (6 * 6))) = 24
[No.10] (2 * (4 + 4)) + 3 = 19
[No.11] 2 + (4 + (7 + (9 / 9))) = 14
[No.12] 3 + (4 + (7 / (8 + (8 - 9)))) = 8
[No.13] 1 + (4 / (3 / 6)) = 9
[No.14] 2 + ((9 / 3) + 9) = 14
[No.15] 1 * (3 + (4 + (3 * 5))) = 22
[No.16] 1 * (6 - (4 - 6)) = 8
[No.17] 1 * (1 - (4 - (6 + (6 + 8)))) = 17
[No.18] 4 + (4 / (5 / (7 + 8))) = 16
[No.19] 3 * ((4 / 3) + 7) = 25
[No.20] (2 * (2 - (6 - 8))) + 9 = 17
[No.21] (1 + (9 / 9)) * 8 = 16
[No.22] 2 + (5 + (5 - (6 / (6 - 8)))) = 15
[No.23] 2 + (2 * (3 - (6 - 8))) = 12
[No.24] 6 + (6 - (7 - (8 + 9))) = 22
[No.25] (1 + 8) * (8 - 6) = 18
[No.26] (2 * (5 + (7 - 7))) + 8 = 18
[No.27] (3 * (8 - 3)) + 4 = 19
[No.28] 5 - (9 / (6 - 9)) = 8
[No.29] 1 + ((2 * (3 + (4 + 8))) - 9) = 22
[No.30] 1 * (2 + (7 + 8)) = 17
[No.31] 1 + (1 - (3 - (6 + 9))) = 14
[No.32] 2 / (6 / (7 * 9)) = 21
[No.33] 1 + ((4 * 7) - 6) = 23
[No.34] 1 * (4 - (4 * (6 - 8))) = 12
[No.35] (5 / (3 / 9)) - 1 = 14
[No.36] 1 * (1 + ((3 * (5 + 5)) - 7)) = 24
[No.37] (2 / 2) + (5 + 6) = 12
[No.38] (1 + 8) * (8 - 6) = 18
[No.39] 1 * (3 + (4 + 6)) = 13
[No.40] 2 * (((6 + 6) / 8) + 8) = 19
[No.41] 3 - ((4 / 4) - 9) = 11
[No.42] ((6 - 4) * 9) - 1 = 17
[No.43] 4 + (7 - (8 / 8)) = 10
[No.44] 1 * ((8 - 6) * 9) = 18
[No.45] 3 * (4 - (6 - 8)) = 18
[No.46] 1 * ((2 / (4 / 8)) + 9) = 13
[No.47] 3 * (7 - (8 / 8)) = 18
[No.48] 1 + (2 - (3 - (3 * 6))) = 18
[No.49] 4 + (5 + (9 - (9 / 9))) = 17
[No.50] (6 * 9) - (5 * 7) = 19
[No.51] 3 * (8 - (6 / 6)) = 21
[No.52] 1 - (2 * (7 - (7 + 8))) = 17
[No.53] ((2 / 6) + 6) * 3 = 19
"""
実際に問題を解いた際の処理速度を確認します。
GoogleColaboratory上で以下のコードを動かして、処理速度を出力します。
動作結果は以下のようになりました。Wall timeが合計実行時間になるので、0.84秒で問題が解けていることがわかります。
検証
問題が解けることは確認できましたが、実際に正しいかどうかまで確認できていないので、
pytestで検証コードを作成して実際に確認します。
pytestは事前にインストールしておく必要があります。
インストールコマンドは下記の通りです。
pip install pytest
下記のpytestのコードの詳細な説明はスキップしますが、QUERYに格納されている問題すべてに対して「数式の演算結果」と「指定した値」を比較し、一致しているかどうかを検証するコードとなっています。
import pytest
# ファイル保存した関数およびデータの準備
from sample_input import QUERY
from quizknock_solver import solver
# solverで求めた式から値を計算し、指定した値が作成できてるかをテスト
@pytest.mark.parametrize("no, input_nums, create_num", QUERY)
def test_solver(no, input_nums, create_num):
# 解となる数式を求める(Noneは解なしとなります)
formula = solver(input_nums, create_num)
# 解なしの場合はNG
assert formula != None
# 求めた数式を実際に計算する
result = eval(formula)
# 計算結果と指定した値が一致しない場合NG
assert result == create_num
以下のコマンドでテストコードを実行できます。
pytest test_quizknock_solver.py
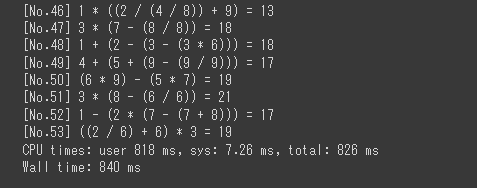
結果は下記の画像のようになり、53問の問題で答えがあっていることが確認できました。
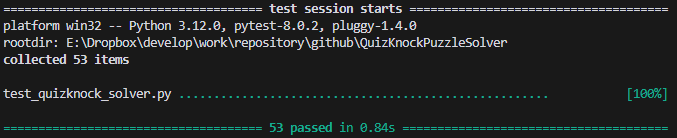
これにて、簡易的な検証含めて実装が完了となります。
おわりに
今回は、とある動画に出てきた問題を解くコードを実装しました。今回の実装では逆ポーランド記法が肝だったと思います。逆ポーランド記法は初めて実装しましたが、簡単に実装できるんだなと感じました。また、逆ポーランド記法とDFSで数式全探索ができるのを確認できたのは良かったかなと思ったりしてます。(競プロでは出てこなさそうですが、、)
Appendix
作成したソースコートはGitHubにアップロードしました。
下記リポジトリを参照ください。