// 競技プログラミング Advent Calendar 2023 の 22 日目の記事です。
// C# Advent Calendar 2023 シリーズ 2 の 22 日目の記事です。
mex とは
11 月のトヨタシステムズプログラミングコンテスト 2023 (AtCoder Beginner Contest 330) で、mex に関する問題が出題されました。
数列の値を 1 つ更新するたびに mex を順次求めるというものです。
ここでまず、mex の定義を確認しておきましょう。
Wikipedia によれば、順序集合に対する mex とは、「minimum excluded value」からなる言葉で、補集合の最小値を指します。
競技プログラミングでは、非負整数の集合 (または数列) に対して mex を求めることが多いです。また、集合が同じ値を 2 個以上含む可能性があることにも注意が必要です (多重集合)。
本稿では、既存のデータ構造を利用して、非負整数の集合に対する mex を効率よく求めるためのクラスを実装していきます。
(非多重) 集合に対する実装
まず、値の重複を許さない (非多重の) 非負整数の集合に対して mex を求める方法を考察しましょう。
定義通りに考えれば、元の集合に含まれていない非負整数の集合を作り、その最小値を求めることになりますが、元の集合に含まれていない非負整数は無限にあり、現実的に直接管理することができません。
しかしよく考えると、ある整数 $M$ に対して、集合の要素数が最大でも $M$ にしかならないとわかっているとき、その mex は最大でも $M$ にしかなりません。したがって、元の集合に含まれていない非負整数を半開区間 $[0, M)$ の範囲のみで保持しておけば十分です。
例えば、 $M=6$ で元の集合が $\{ 0, 3, 4, 7, 8\}$ のとき、集合 $\{1, 2, 5\}$ を保持しておくことになります。ここで、元の集合に要素 $5$ を追加すれば保持する集合は $\{1, 2\}$ に変化し、続けてさらに要素 $4$ を削除すれば保持する集合は $\{1, 2, 4\}$ に変化します。
次のソースコードは、これをクラスとして実装したものです。言語は C# です。
SortedSet<T> は、C++ の std::set に相当します。
他の言語でも適宜読み換えてください。
// ImplicitUsings: enable
[System.Diagnostics.DebuggerDisplay("Mex = {Mex}")]
public class MexSet
{
readonly int max;
readonly SortedSet<int> ex;
public MexSet(int max)
{
this.max = max;
ex = new SortedSet<int>(Enumerable.Range(0, max));
}
public int Mex => ex.Count == 0 ? max : ex.Min;
public bool Add(int value)
{
if (value < 0 || max <= value) return false;
return ex.Remove(value);
}
public bool Remove(int value)
{
if (value < 0 || max <= value) return false;
return ex.Add(value);
}
}
順序付き集合のデータ構造である SortedSet<int> 型のフィールド ex を用意し、元の集合に含まれていない非負整数の集合を管理します。
元の集合に要素が追加されたとき Remove し、削除されたとき Add すればよいです。
mex を求めるには、Min を取得するだけです。
以上で、初期化は時間計算量 $O(M \log M)$ で、要素の追加、削除、mex の取得はすべて時間計算量 $O( \log M)$ でできるようになりました。
なお、範囲外の値が入力された場合、ここでは false を返していますが、例外を投げる仕様にしてもよいと思います。
多重集合に対する実装
上のソースコードを拡張して、今度は多重集合に対する実装を考えます。
例えば、 $M=6$ で元の集合が $\{0, 3, 3, 4, 6\}$ であれば ex は $\{1, 2, 5\}$ ですが、 $3$ が 2 個あるため、 $3$ を 2 回削除してはじめて ex に $3$ が追加されることになります。
逆に、既に含まれている $0, 3, 4$ を追加しても ex は変化しません。
したがって、元の集合に各要素が含まれる個数 (重複数) を管理する必要があり、フィールド counts を用意します。
元の集合に含まれていない非負整数の集合 ex は、相変わらず非多重集合の SortedSet<int> で管理することができます。
時間計算量のオーダーは非多重集合のときと同じです。
// ImplicitUsings: enable
[System.Diagnostics.DebuggerDisplay("Mex = {Mex}")]
public class MexMultiSet
{
readonly int max;
readonly int[] counts;
readonly SortedSet<int> ex;
public MexMultiSet(int max)
{
this.max = max;
counts = new int[max];
ex = new SortedSet<int>(Enumerable.Range(0, max));
}
public int Mex => ex.Count == 0 ? max : ex.Min;
public bool Add(int value)
{
if (value < 0 || max <= value) return false;
if (counts[value]++ == 0) ex.Remove(value);
return true;
}
public bool Remove(int value)
{
if (value < 0 || max <= value) return false;
if (counts[value] == 0) return false;
if (--counts[value] == 0) ex.Add(value);
return true;
}
}
ちなみに、Add と Remove のように対の関係となっている概念に対して、if (a[i]++ == 0) と if (--a[i] == 0) のように対となる実装パターンがたまに現れます。
さて、これで mex に関するライブラリが完成し、ABC 330 E に簡単に正解できるようになりました。
固定長の数列の要素を変更するには、削除して追加すればよいです:
優先度付きキューを利用した実装
SortedSet<T> のような順序付き集合は、通常は平衡二分探索木で実装されていますが、このデータ構造は少し重いです。
そこで、他のデータ構造で mex の計算を実現できないかを考えていくと、必要な機能は「要素の追加」「要素の削除」「最小値の取得」のみのため、例えば「削除機能を持った優先度付きキュー (データ構造は主に二分ヒープ)」があれば十分ということになります。
「削除機能を持った優先度付きキュー」は、一般には「通常の (削除機能を持たない) 優先度付きキュー」と「要素数を管理するための連想配列 (.NET では Dictionary<T, int>)」があれば実現できます。(追記: 削除可能な優先度付きキューを書きました。)
今回はさらに、管理するキーが $[0, M)$ の範囲の整数と限定されているため、連想配列の代わりに int[] を利用します。
ソースコードは次のようになります。
// ImplicitUsings: enable
[System.Diagnostics.DebuggerDisplay("Mex = {Mex}")]
public class MexMultiSet
{
readonly int max;
readonly int[] counts;
readonly IntPQSet ex;
public MexMultiSet(int max)
{
this.max = max;
counts = new int[max];
ex = new IntPQSet(max, Enumerable.Range(0, max));
}
public int Mex => ex.Count == 0 ? max : ex.Min;
public bool Add(int value)
{
if (value < 0 || max <= value) return false;
if (counts[value]++ == 0) ex.Remove(value);
return true;
}
public bool Remove(int value)
{
if (value < 0 || max <= value) return false;
if (counts[value] == 0) return false;
if (--counts[value] == 0) ex.Add(value);
return true;
}
}
// 削除機能を持った優先度付きキュー
class IntPQSet : PriorityQueue<int, int>
{
readonly int[] counts;
public IntPQSet(int max, IEnumerable<int> items)
{
counts = new int[max];
if (items != null) foreach (var v in items) Add(v);
}
public int Min => Peek();
public bool Add(int item)
{
Enqueue(item, item);
++counts[item];
return true;
}
public bool Remove(int item)
{
if (counts[item] == 0) return false;
--counts[item];
EnsureMin();
return true;
}
void EnsureMin()
{
while (Count > 0 && counts[Peek()] == 0) Dequeue();
}
}
「削除機能を持った優先度付きキュー」を、PriorityQueue<TElement, TPriority> を継承した IntPQSet クラスとして実装しました。
SortedSet<int> と同じ使い勝手になるように、Min, Add, Remove を備えています。
これにより、MexMultiSet クラスを前節からほぼ修正せずに済んでいます。
IntPQSet の任意の要素の削除は直接できないため、遅延評価により行います。すなわち、優先度付きキューの先頭の要素が削除済 (要素数が 0) になっていればデキューします。
この IntPQSet の時間計算量は、サイズを $n$ としたとき Min は $O(1)$ 、Add は $O( \log n)$ 、そして Remove は最悪 $O(n \log n)$ ですが償却で $O( \log n)$ となります。
したがって、MexMultiSet に対して Mex は $O(1)$ 、Add は償却 $O( \log M)$ 、Remove は $O( \log M)$ となります。
ABC 330 E への提出も、SortedSet<int> を利用した場合と比較して高速になりました:
他にも、これと同様の発想でセグメント木を利用する方法も考えられます。
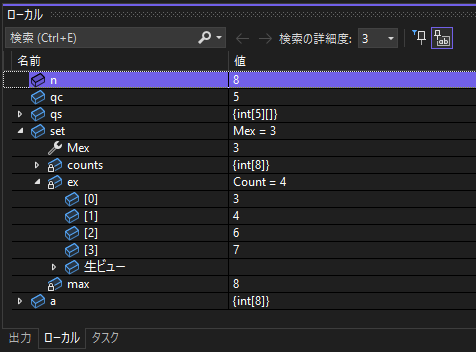
補足: DebuggerDisplay とは
クラスなどに DebuggerDisplay 属性を指定することにより、Visual Studio でデバッグ中に表示する文字列をカスタマイズすることができます。
この例では、Mex = 3 と表示されています。
作成したサンプル
検証したバージョン
- 開発環境: C# 10, .NET 6
-
PriorityQueue<TElement, TPriority>クラスが登場した .NET のバージョン
-
- 実行環境: C# 11, .NET 7
問題集
参照
- Mex (mathematics) - Wikipedia
- SortedSet<T> クラス
- PriorityQueue<TElement,TPriority> クラス
- DebuggerDisplayAttribute クラス
次回: 削除可能な優先度付きキュー