以下、ガウス過程の途中計算から
前回はガウス過程における$\mu(x)$および$\sigma^2(x)$の値を算出した。
これらが分かればブラックボックス関数の最小化$\min_{\mathbf{x}} { f(\mathbf{x}) }$を直接計算することなく関数の予測を行うことができる。
すなわち、以下を求ればいい。
\min_{i} \{ \mu(\mathbf{x}_i) \}
(多変量)ガウス分布とは、そのMAP推定値が丁度、出力$\mu$と等価である。
そのため、$\mu(x)$をブラックボックス関数の代わりに扱うことができる。
多変量ガウスの補足:
p(\mathbf{y}_n) = \frac{1}{\sqrt{(2\pi)^n |\Sigma_n|}}
\exp\left(
-\frac{1}{2} (\mathbf{y}_n - \boldsymbol{\mu}_n)^\top \Sigma_n^{-1} (\mathbf{y}_n - \boldsymbol{\mu}_n)
\right)
以上のように最大値は$y$=$\mu$となることがわかる。
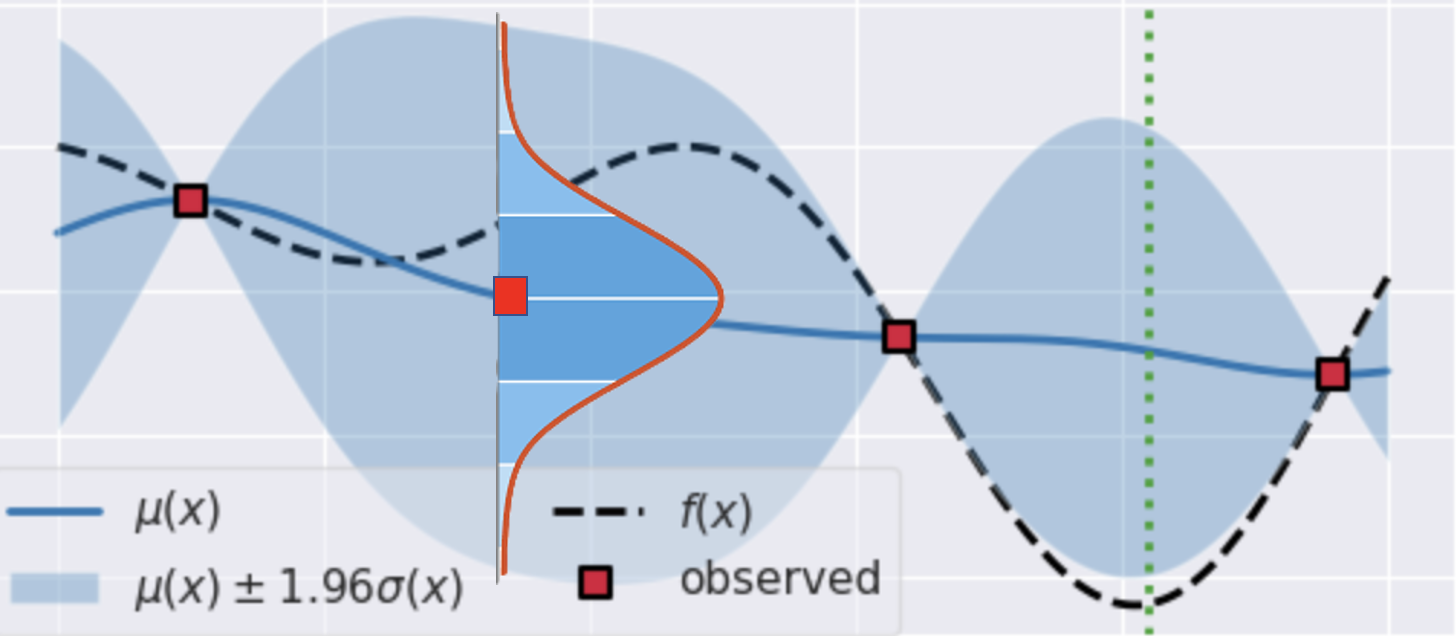
下図のように平均関数(青線)上の点はガウス分布の平均となる。
なお、平均関数を取り囲む水色の大枠はベイズ信用区間を表している。その幅は各点におけるガウス分布の区間幅に対応している。
最適点の求め方について
平均関数と分散関数を求めることができたが、(ブラックボックス関数の代わりである)平均関数の最小値を具体的にどう求めるか。
色々やり方はあるかもしれないが、ここでは獲得関数によって最小値を探索することにする。
獲得関数とは何か?
端的に言うと、最小値などの最適点をどう見つけるかといった方策を表す関数である(と、私は考えている)。
もちろん、状況に応じて適した方策が存在するため、獲得関数はたくさん考えられている。
例として、シンプルな獲得関数を以下に示す。
\alpha(x)
= -\bigl(\mu(x) \;-\; \sqrt{\beta}\,\sigma(x)\bigr)
ただし、\arg_{\max x}\,\alpha(x)
この関数は信頼下限獲得関数と呼ばれる。$\arg_{\max x},\alpha(x)$とあるように、獲得関数が最大となるような変数が平均関数の最適点となる。
この式を見てみると、$\beta$が$\sigma(x)$を調整しているハイパーパラメータであることがわかる。
例えば、$\beta$がゼロなら、獲得関数は$\mu(x)$のみに依存する。これが意味することは、平均関数そのものを最小化すればいいことになる。一方、$\beta$に値があれば、$\sigma(x)$も考慮した最大化がなされる。
前者の場合、今まで得たデータから最適点を求めるが、一方、後者では、分散関数という不確実性の振れ幅を考慮した探索となる。
つまり、獲得関数とは利用と探索のトレードオフの関係になっているのだ。
繰り返すと、今まで学習したデータから最適点を見つけてしまうのか、まだまだ怪しい領域があると思い探索していくのか
このことを表現している。
そして、このような獲得関数を持ってガウス過程における最適点を探すことをベイズ最適化と呼ぶ。