この記事では最終的に、次のことを確認します。
「多項式フィッティングにおいて二乗和誤差を用いたフィッティング」は、「観測ノイズとして正規分布を仮定した多項式モデルに対して最尤推定を適用した結果」と一致する
内容としてはそれほど高度ではなく、専門書では最初の方に載っている話のようです。わざわざこのQiita記事を書くのは
- 2つは別の定義から出発しており、「結局同じことをやっていた」という関係が意外
- 素朴な二乗和誤差という考え方が、統計学の世界でどういう意味を持つかという視点を与えてくれる
という点が面白いと思ったからですが……基本的とはいえ専門用語が多いので、順番に述べていきます。
ただし、前提知識があまりにもたくさん必要だったので
- 確率変数
- 確率密度関数
- 正規分布
の基本については既知のものとします(筆者もあんまりよく分かってませんが)。これらについては既存の分かりやすい説明がたくさんあるかと思います。それ以外については、高校で習う程度の数学知識で済むはずです。
フィッティング / 多項式フィッティング
フィッティングとは
2つの変量 $x, y$ についての関係を、なんらかの数式で表すことを モデル化 といい、モデルに含まれる係数を観測結果から求めることを(この記事では) フィッティング といいます。特に $y$ が連続的な量(例えば、温度や長さなど)のとき、回帰ともいいます。うまくモデルを選びフィッティングできたなら、未知の $x$ についても $y$ がどれぐらいになるかを予測できて便利というわけです。実用上さまざまな応用が考えられます。
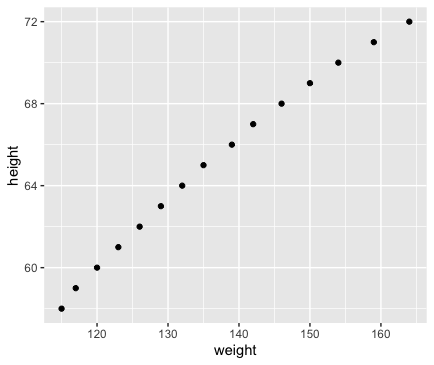
例として、これはある集団の身長と体重の組をプロットしたものです1。
観測されたこのデータを回帰分析(以降で説明される手法と同質のものです)にかけることで、おおむね $\rm{height} = 0.2872 \times \rm{weight} + 25.7235$ という関係を得ます。これがつまり2つの変量をモデル化し、フィッティングしたということです。
Rでの実行例を示しておきます。
> lm(formula = height ~ weight, women)
Call:
lm(formula = height ~ weight, data = women)
Coefficients:
(Intercept) weight
25.7235 0.2872
例では1つの重み係数と定数項を使ったモデルを用いていますが、以降この記事ではモデルに $D$ 次の多項式を用います。つまり、2つの関係は多項式で表せると仮定します。モデルはあくまで(単純化された)仮説に過ぎません。
y = w_0 + w_1 x + w_2 x^2 + \cdots + w_D x^D
$D$ はフィッティングによって求めるパラメータではなくモデルそのもののパラメータで、仮説として事前に人間が与える値です。具体的にいくつの値がいいかは $x, y$ の関係性に依存した難しい問題になるのですが、この記事の本題ではないので触れません。
まとめると、 $x, y$ の関係を多項式で表し、その際の重み $\boldsymbol{w} = \lbrace w_0, \dots, w_D \rbrace$ の値を具体的に計算で求めるのが、この記事でいうフィッティングです。
具体的な係数の求め方
モデルは $D$ 次の多項式なので、 $x, y$ の観測値の組が $D+1$ 個あれば係数を定めることができ……ますが、あまり汎用性がありません。
- 観測データがぴったり $D+1$ 個ということはまずない。データ数は普通もっとずっと多い
- 実際上、観測した $x, y$ にはノイズが含まれていることがほとんどである
- つまり、真の値からずれた値しか観測によって得られない
- そもそもモデルはあくまで近似なので、当てはまりの良し悪しはあれど「ぴったり合う」ことはまずない
そこで、係数の決定には二乗和誤差の最小化というものを考えます。
\begin{align}
E &= \sum_{n=1}^N (y_n - f(x_n))^2 \\
f(x) &= w_0 + w_1 x + w_2 x^2 + \cdots + w_D x^D
\end{align}
で定義される二乗和誤差$E$を最小化するような $\boldsymbol{w}$ を発見する問題として解きます(最小二乗法とも呼ぶようです)。ただし $N$ はデータ数、 $x_n, y_n$ はそれぞれn番目の $x, y$ を表します。
$E$ の最小化問題は解析的に(=数式をがんばって変形していくと)解けることが知られていますが、これについても省略します。詳細は参考書籍などを参照ください。
最尤推定
あるパラメータ未知の確率モデルのもとで観測値が得られたとき、観測値が出てくる確率を最大化するようにパラメータを選ぶことを、 最尤推定 といいます。
何を言っているのか抽象的で掴みづらいので、具体例で考えます。
コイン投げを考えます。コインは1回投げるたびに表が確率 $\theta$ で、裏が確率 $1-\theta$ で出るとします(ただし $0 \le \theta \le 1$ )。コインを10回投げて表が8回出たとき、 $\theta$ はいくつだと推定できるかという問題を考えてみます。
コインを10回投げたときに表が8回出る確率 $L$ を、 $\theta$ を用いて表します2。コインを投げる試行は互いに影響がないとすると
L = {}_{10} \mathrm{C}_8 \times \theta^8 (1 - \theta)^2
です(反復試行の確率というやつです)。実際にコインを投げてこうなったということは、「こうなる確率が最大となるような $\theta$ であった」と推測するのが最尤推定なので、上式$L$の最大値となるような $\theta$ の値を調べます。
式を解くのは手間なのでWolfram Alphaを使うと $\theta=4/5$ のとき最大値となることが分かります。
https://www.wolframalpha.com/input/?i=maximize+(10+combination+8)+*+x%5E8+*+(1-x)%5E2,+0+%3C%3D+x+%3C%3D+1
この結論は、「10回中8回が表なら、コインの表が出る確率は $\theta = 8/10 = 4/5$ なのでは?」という素朴な直感と一致するものです。コイン投げぐらいだとあまり面白みのある結果は得られないですが、もっと複雑な確率分布に対しても最尤推定は適用できます。
$L$ の最大値を考える代わりに、対数をとった $\log L$ の最大値を考えることがあります。対数関数は単調増加する関数なので、対数をとっても最大化としては等しく、かつ式が簡単になることがあります。
記事の主題: さっそく多項式モデルに最尤推定を適用してみる
ようやく本題です。平均 $\mu$ 分散 $\sigma^2$ である正規分布の確率密度関数を $\mathcal{N}(x \mid \mu, \sigma^2)$ と表記することにします。すると、観測ノイズとして正規分布が乗った多項式モデルは、次のように定式化できます。
\begin{align}
p(y) &= \mathcal{N}(y \mid f(x), \sigma^2) \\
f(x) &= w_0 + w_1 x + w_2 x^2 + \cdots + w_D x^D
\end{align}
なぜなら、観測ノイズが乗っているということは、「平均は多項式モデルに従っている分散未知の正規分布」に従っていると言い換えられるからです。
観測データが $\boldsymbol{x}=\lbrace x_i \rbrace,\boldsymbol{y}=\lbrace y_i \rbrace$ の形で $N$ 個与えられているとして最尤推定を適用し $\boldsymbol{w}$ を決定します。まず $L$ を定義してからそれを最大化するのでした。
ただし、観測値 $x_i, y_i$ は互いに独立している(影響を及ぼさない)ものとします3。 $L$ はそれぞれの観測値の積になることから
\begin{align}
L &= \prod_{n=1}^N \mathcal{N}(y_n \mid f(x_n), \sigma^2) \\
&= \prod_{n=1}^N \frac{1}{\sqrt{2\pi \sigma^2}} \exp \! \left( -\frac{(y_n - f(x_n))^2}{2\sigma^2} \right)
\end{align}
です。式を簡略化するために対数を取ります。
\begin{align}
\log L &= \sum_{n=1}^N \log ( \frac{1}{\sqrt{2\pi \sigma^2}} \exp \! \left( -\frac{(y_n - f(x_n))^2}{2\sigma^2} \right) ) \\
&= \sum_{n=1}^N \log \frac{1}{\sqrt{2\pi \sigma^2}} - \sum_{n=1}^N (y_n - f(x_n))^2 + \sum_{n=1}^N 2\sigma^2
\end{align}
さて、いま $L$ を最大化するための $\boldsymbol{w}$ について考えているので、 $f$ を含む第2項のみに関心があります(他の項は定数です)。第2項の最大化とは、符号を反転させた
\sum_{n=1}^N (y_n - f(x_n))^2
の最小化に他ならず、これはまさに二乗和誤差の最小化と等価です。
まとめ
二乗和誤差が統計学の世界でどういう解釈ができるのかを紹介しました。
二乗和誤差はとても単純そう(最初に思いつくのでは? というぐらいシンプルな発想だと思います)ですが、ちゃんと理論的解釈ができるのは興味深いことだと思います。
ちなみに、過剰適合を抑えるために二乗和誤差にペナルティ項を加えるという回帰の改善方法(リッジ回帰)が知られていますが、これは確率モデルの視点で見ると、重みの事前分布として正規分布を仮定するのと等価らしいです。それについても参考書籍では触れられていました。