はじめに
制約プログラミング(Constraint Programming)はプログラミングパラダイムの一つです。 制約プログラミングにおいては、変数間の関係を制約という形で記述することによりプログラムを記述します。
現在ではAIと言えばディープラーニングと同義のように言われたりしますが、かつてはこの制約プログラミングや数式処理などもAIと呼ばれていました。
Javaで制約プログラミングのライブラリを実装し、エイト・クイーン、覆面算、数独などの問題を解いてみます。
対象とする問題
最も単純な問題を対象とします。具体的には以下のような問題です。
- 変数の定義域は整数のみとします。
- 変数の定義域は有限で、その範囲は問題の中で定義されているものとします。
簡単な例題
説明のために簡単な例題を考えてみます。
- 式 a + b = c を満たす変数a, b, cの値を求めてください。
- ただし a < b とします。
- 変数a, b, cの定義域は{1, 2, 3}とします。
アプローチ
各変数の定義域の値ごとに制約を満たす組み合わせを見つければよいので、単純な3重ループのプログラムを考えてみます。Javaで表現するとこんな感じです。
for (int a : List.of(1, 2, 3))
for (int b : List.of(1, 2, 3))
for (int c : List.of(1, 2, 3))
if (a < b)
if (a + b == c)
answer(a, b, c);
answerは解が見つかった時点で呼び出されるコールバック関数です。
このプログラムでは入れ子になったforループの最内部は 3 x 3 x 3 = 27回実行されます。
処理効率を考えるとこれを少し改善することができます。制約a < bは変数aおよびbの値が確定した時点でチェックすることができるので、以下のように書き換えることができます。
for (int a : List.of(1, 2, 3))
for (int b : List.of(1, 2, 3))
if (a < b)
for (int c : List.of(1, 2, 3))
if (a + b == c)
answer(a, b, c);
a < bを満たす(a, b)の組み合わせは(1, 2), (1, 3), (2, 3)の3通りしかありません。この3通りに対してfor (int c : List.of(1, 2, 3))がそれぞれ実行されるので、入れ子になったforループの最内部は 3 x 3 = 9回で済むことになります。前述のコードと比べると約3倍の処理性能が期待できます。制約のチェック回数も減るのでもっと速くなるかもしれません。
このアプローチでプログラムを構成してみましょう。
まとめるとこうなります。
- 各変数に定義域の値を順次代入するループを入れ子にします。
- 制約はなるべく外側のループ内でチェックすることにより効率を上げます。
- 解が見つかった時点でコールバック関数を呼び出します。
モデル
クラスの候補としては以下が考えられます。
- 問題 (Problem)
解くべき問題のクラスです。 - 変数 (Variable)
問題に表れる変数です。 - 定義域 (Domain)
各変数の定義域です。 - 制約 (Constraint)
変数が満たすべき制約式です。 - 制約式(Predicate)
制約式をラムダ式で表現するための関数型インタフェースです。 - 問題解決 (Solver)
問題を解きます。 - 解 (Answer)
解が見つかったときに呼び出されるコールバックです。
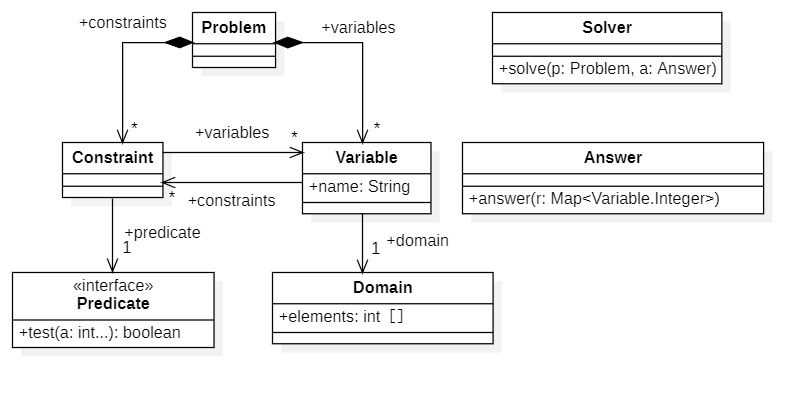
UMLのクラス図として表現するとこのようになります。
コード
Domain(定義域)は不変な整数のリストです。
public class Domain extends AbstractList<Integer> {
private final int[] elements;
private Domain(int... elements) {
this.elements = elements;
}
public static Domain of(int... elements) {
return new Domain(Arrays.copyOf(elements, elements.length));
}
public static Domain range(int startInclusive, int endExclusive) {
return new Domain(IntStream.range(startInclusive, endExclusive).toArray());
}
public static Domain rangeClosed(int startInclusive, int endInclusive) {
return range(startInclusive, endInclusive + 1);
}
@Override public Integer get(int index) { return elements[index]; }
@Override public int size() { return elements.length; }
}
変数(Variable)は名称(name)と定義域(Domain)を持つクラスです。
その変数に係るすべての制約(Constraint)への参照を保持しています。
インスタンスの生成は問題(Problem)のファクトリメソッドで行うため、コンストラクタはパッケージスコープとします。
public class Variable {
public final String name;
public final Domain domain;
private final List<Constraint> _constraints = new ArrayList<Constraint>();
public final List<Constraint> constraints = Collections.unmodifiableList(_constraints);
Variable(String name, Domain domain) {
this.name = name;
this.domain = domain;
}
void add(Constraint constraint) {
this._constraints.add(constraint);
}
@Override
public String toString() {
return name;
}
}
制約式(Predicate)は制約を式で表現するための関数インタフェースです。
制約に係るすべての変数の値が束縛されたときに各変数の値を引数として呼び出されるtest(int...)メソッドのみが定義されています。
これを使用することで制約式をラムダ式で表現することができます。
@FunctionalInterface
public interface Predicate {
boolean test(int... values);
}
制約(Predicate)は制約式(Predicate)と制約に係る変数への参照を持つ不変のクラスです。
インスタンスの生成は問題(Problem)のファクトリメソッドで行うので、コンストラクタはパッケージスコープとします。
public class Constraint {
public final Predicate predicate;
public final List<Variable> variables;
Constraint(Predicate predicate, Variable... variables) {
this.predicate = predicate;
this.variables = List.of(variables);
}
@Override
public String toString() {
return "制約" + variables;
}
}
問題(Problem)は関連するすべての変数と制約を持つクラスです。
変数の定義はvariable(String, Domain)で行います。
制約の定義はconstraint(Predicate, Variable...)で行います。
複数の変数について、どの二つの変数も値が異なるという制約を簡易に表現するためのメソッドallDifferent(Variable...)があります。
public class Problem {
private List<Variable> _variables = new ArrayList<>();
public List<Variable> variables = Collections.unmodifiableList(_variables);
private Map<String, Variable> variableMap = new HashMap<>();
private List<Constraint> _constraints = new ArrayList<>();
public List<Constraint> constraints = Collections.unmodifiableList(_constraints);
public Variable variable(String name, Domain domain) {
if (variableMap.containsKey(name))
throw new IllegalArgumentException("変数名が重複: " + name);
Variable v = new Variable(name, domain);
this._variables.add(v);
this.variableMap.put(name, v);
return v;
}
public Variable variable(String name) {
return variableMap.get(name);
}
public Constraint constraint(Predicate predicate, Variable... variables) {
Constraint c = new Constraint(predicate, variables);
for (Variable v : variables)
v.add(c);
this._constraints.add(c);
return c;
}
public void allDifferent(Variable... variables) {
for (int i = 0, size = variables.length; i < size; ++i)
for (int j = i + 1; j < size; ++j)
constraint(a -> a[0] != a[1], variables[i], variables[j]);
}
}
解(Answer)は見つかった解を受け取るためのコールバック関数です。
変数と値の対をMapとして受け取ります。
実質的に関数インタフェースなのでラムダ式でコールバック関数を記述することができます。
public interface Answer {
void answer(Map<Variable, Integer> result);
}
問題解決(Solver)は問題(Problem)から解を見つけるsolve(Problem, Answer)メソッドを持っています。
変数の数は可変なので冒頭に記述したようなfor文のネストで束縛を実現することはできないので、再起呼び出しによって束縛を行います。
オーバーロードされたsolve(Problem, List<Variable>, Answer)メソッドは問題を解く時に変数を束縛する順序をList<Variable>で指定することができます。
内部staticメソッドconstraintOrder(List<Variable>, List<Constraint>)は変数の束縛順序から適用可能な制約(Constraint)の順序を求めます。
public class Solver {
static final Logger logger = Logger.getLogger(Solver.class.getName());
static List<List<Constraint>> constraintOrder(List<Variable> bindingOrder, List<Constraint> constraints) {
int variableSize = bindingOrder.size();
int constraintSize = constraints.size();
List<List<Constraint>> result = new ArrayList<>(variableSize);
Set<Constraint> done = new HashSet<>(constraintSize);
Set<Variable> bound = new HashSet<>(variableSize);
for (Variable v : bindingOrder) {
bound.add(v);
List<Constraint> list = new ArrayList<>();
result.add(list);
for (Constraint c : constraints)
if (!done.contains(c) && bound.containsAll(c.variables)) {
list.add(c);
done.add(c);
}
}
return result;
}
public void solve(Problem problem, List<Variable> bindingOrder, Answer answer) {
int variableSize = problem.variables.size();
List<List<Constraint>> constraintOrder = constraintOrder(bindingOrder, problem.constraints);
int[] arguments = new int[variableSize];
Map<Variable, Integer> result = new LinkedHashMap<>(variableSize);
new Object() {
boolean test(int i) {
for (Constraint c : constraintOrder.get(i)) {
int p = 0;
for (Variable v : c.variables)
arguments[p++] = result.get(v);
if (!c.predicate.test(arguments))
return false;
}
return true;
}
void solve(int i) {
if (i >= variableSize)
answer.answer(result);
else {
Variable v = bindingOrder.get(i);
Domain d = v.domain;
for (int value : d) {
result.put(v, value);
if (test(i))
solve(i + 1);
}
}
}
}.solve(0);
}
public void solve(Problem problem, Answer answer) {
solve(problem, problem.variables, answer);
}
}
テスト
冒頭の簡単な例を実際に解いてみます。
Problem problem = new Problem();
Domain domain = Domain.of(1, 2, 3);
Variable A = problem.variable("A", domain);
Variable B = problem.variable("B", domain);
Variable C = problem.variable("C", domain);
Constraint X = problem.constraint(a -> a[0] + a[1] == a[2], A, B, C);
Constraint Y = problem.constraint(a -> a[0] < a[1], A, B);
Solver solver = new Solver();
solver.solve(problem, result -> System.out.println(result));
結果はこうなりました。
{A=1, B=2, C=3}
変数の束縛順と制約の適用順は以下のようになっています。
0: A []
1: B [制約[A, B]]
2: C [制約[A, B, C]]
エイト・クイーン
エイト・クイーン - Wikipediaはチェスの盤上に、8個のクイーンを配置する問題です。このとき、どの駒も他の駒に取られるような位置においてはいけません。
クイーンの動きは、上下左右斜めの8方向に、遮る物がない限り進めます。将棋の飛車と角行を合わせた動きです。一辺のマスをnとした変形版を「n-クイーン」パズルといいます。
定義域が$\{1..n\}$であるような変数をn個用意して、それぞれが互いに異なり、斜めにも重ならないようにする問題として解きます。
ここでは$n ∊ \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}$について、それぞれの解の個数を求めてみます。
class TestNQueens {
static Logger logger = Logger.getLogger(TestNQueens.class.getName());
static int nQueens(final int n) {
long start = System.currentTimeMillis();
Problem problem = new Problem();
Domain domain = Domain.range(0, n);
Variable[] rows = IntStream.range(0, n)
.mapToObj(i -> problem.variable("R" + i, domain))
.toArray(Variable[]::new);
for (int i = 0; i < n; ++i)
for (int j = i + 1; j < n; ++j) {
int distance = j - i;
problem.constraint(
(x, y) -> x != y && Math.abs(x - y) != distance, rows[i], rows[j]);
}
Solver solver = new Solver();
int[] answers = {0};
solver.solve(problem, m -> ++answers[0]);
logger.info("n=" + n + " : answers=" + answers[0]
+ " : elapse=" + (System.currentTimeMillis() - start) + "ms.");
return answers[0];
}
@Test
void test() {
assertEquals(1, nQueens(1));
assertEquals(0, nQueens(2));
assertEquals(0, nQueens(3));
assertEquals(2, nQueens(4));
assertEquals(10, nQueens(5));
assertEquals(4, nQueens(6));
assertEquals(40, nQueens(7));
assertEquals(92, nQueens(8));
assertEquals(352, nQueens(9));
assertEquals(724, nQueens(10));
}
}
結果はこんな感じです。Wikipediaの記述と一致しました。
2020-05-19T16:31:06.863 情報 n=1 : answers=1 : elapse=27ms.
2020-05-19T16:31:06.941 情報 n=2 : answers=0 : elapse=3ms.
2020-05-19T16:31:06.942 情報 n=3 : answers=0 : elapse=0ms.
2020-05-19T16:31:06.944 情報 n=4 : answers=2 : elapse=0ms.
2020-05-19T16:31:06.947 情報 n=5 : answers=10 : elapse=2ms.
2020-05-19T16:31:06.953 情報 n=6 : answers=4 : elapse=5ms.
2020-05-19T16:31:06.963 情報 n=7 : answers=40 : elapse=10ms.
2020-05-19T16:31:06.984 情報 n=8 : answers=92 : elapse=20ms.
2020-05-19T16:31:07.031 情報 n=9 : answers=352 : elapse=45ms.
2020-05-19T16:31:07.118 情報 n=10 : answers=724 : elapse=87ms.
覆面算
次に覆面算を解いてみます。有名なSEND MORE MONEYです。各英字に1桁の数字を割り当てて式が成立するようにします。同じ英字は同じ数字、異なった英字は異なった数字、先頭の数字はゼロ以外とします。
SEND
+ MORE
------
MONEY
static Logger logger = Logger.getLogger(TestSendMoreMoney.class.getName());
static int number(int... digits) {
return IntStream.of(digits).reduce(0, (t, d) -> t * 10 + d);
}
@Test
public void test単一制約() {
Problem problem = new Problem();
Domain first = Domain.of(1, 2, 3, 4, 5, 6, 7, 8, 9);
Domain rest = Domain.of(0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
Variable S = problem.variable("S", first);
Variable E = problem.variable("E", rest);
Variable N = problem.variable("N", rest);
Variable D = problem.variable("D", rest);
Variable M = problem.variable("M", first);
Variable O = problem.variable("O", rest);
Variable R = problem.variable("R", rest);
Variable Y = problem.variable("Y", rest);
Variable[] variables = {S, E, N, D, M, O, R, Y};
problem.allDifferent(variables);
problem.constraint(a ->
number(a[0], a[1], a[2], a[3]) + number(a[4], a[5], a[6], a[1])
== number(a[4], a[5], a[2], a[1], a[7]), variables);
Solver solver = new Solver();
solver.solve(problem, m -> logger.info(m.toString()));
}
結果はこうなりました。
{S=9, E=5, N=6, D=7, M=1, O=0, R=8, Y=2}
この解き方は制約が一つしかなく、すべての変数が束縛された後にチェックされます。つまり最も内側のループ内で制約のチェックが行われるのであまり効率がよくありません。私の環境では2秒弱かかりました。
桁上がりの変数を追加して、各桁ごとに制約を定義するようにすると少し速くなります。
@Test
public void test桁ごとの制約() {
Domain zero = Domain.of(0);
Domain first = Domain.of(1, 2, 3, 4, 5, 6, 7, 8, 9);
Domain rest = Domain.of(0, 1, 2, 3, 4, 5, 6, 7, 8, 9);
Domain carry = Domain.of(0, 1);
Problem problem = new Problem();
Variable Z = problem.variable("Z", zero);
Variable C1 = problem.variable("C1", carry);
Variable C2 = problem.variable("C2", carry);
Variable C3 = problem.variable("C3", carry);
Variable C4 = problem.variable("C4", carry);
Variable S = problem.variable("S", first);
Variable E = problem.variable("E", rest);
Variable N = problem.variable("N", rest);
Variable D = problem.variable("D", rest);
Variable M = problem.variable("M", first);
Variable O = problem.variable("O", rest);
Variable R = problem.variable("R", rest);
Variable Y = problem.variable("Y", rest);
Variable[] variables = {S, E, N, D, M, O, R, Y};
problem.allDifferent(variables);
// C4 C3 C2 C1 Z
// Z S E N D
// + Z M O R E
// ---------------
// M O N E Y
Predicate digitPredicate = a -> a[0] + a[1] + a[2] == a[3] + a[4] * 10;
problem.constraint(digitPredicate, Z, D, E, Y, C1);
problem.constraint(digitPredicate, C1, N, R, E, C2);
problem.constraint(digitPredicate, C2, E, O, N, C3);
problem.constraint(digitPredicate, C3, S, M, O, C4);
problem.constraint(digitPredicate, C4, Z, Z, M, Z);
Solver solver = new Solver();
solver.solve(problem, m -> logger.info(m.toString()));
}
0.3秒くらいで解けるようになりました。
数独
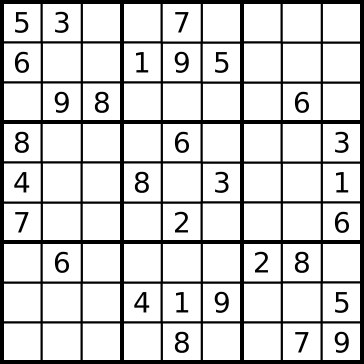
数独 - Wikipediaの最初にある問題を解いてみます。
static Logger logger = Logger.getLogger(Test数独.class.toString());
static int 辺の長さ = 9;
static int 小四角形の辺の長さ = 3;
static Domain 定義域 = Domain.rangeClosed(1, 9);
static String 名前(int r, int c) {
return r + "@" + c;
}
static Variable[][] 変数定義(Problem 問題, int[][] 入力) {
Variable[][] 変数 = new Variable[辺の長さ][辺の長さ];
for (int r = 0; r < 辺の長さ; ++r)
for (int c = 0; c < 辺の長さ; ++c)
変数[r][c] = 問題.variable(名前(r, c),
入力[r][c] == 0 ? 定義域 : Domain.of(入力[r][c]));
return 変数;
}
static List<Variable[]> 制約定義(Problem 問題, Variable[][] 変数) {
List<Variable[]> 制約変数 = new ArrayList<>();
for (int r = 0; r < 辺の長さ; ++r)
制約変数.add(変数[r]);
for (int c = 0; c < 辺の長さ; ++c) {
Variable[] va = new Variable[辺の長さ];
制約変数.add(va);
for (int r = 0; r < 辺の長さ; ++r)
va[r] = 変数[r][c];
}
for (int r = 0; r < 辺の長さ; r += 小四角形の辺の長さ)
for (int c = 0; c < 辺の長さ; c += 小四角形の辺の長さ) {
Variable[] va = new Variable[辺の長さ];
制約変数.add(va);
for (int i = 0, p = 0; i < 小四角形の辺の長さ; ++i)
for (int j = 0; j < 小四角形の辺の長さ; ++j, ++p)
va[p] = 変数[r + i][c + j];
}
for (Variable[] va : 制約変数)
問題.allDifferent(va);
return 制約変数;
}
static void 答(Variable[][] 変数, Map<Variable, Integer> 解答) {
for (int r = 0; r < 辺の長さ; ++r) {
StringBuilder sb = new StringBuilder();
for (int c = 0; c < 辺の長さ; ++c)
sb.append(String.format("%2d", 解答.get(変数[r][c])));
logger.info(sb.toString());
}
}
static void 数独束縛順序指定なし(int[][] 入力) {
Problem 問題 = new Problem();
Variable[][] 変数 = 変数定義(問題, 入力);
制約定義(問題, 変数);
Solver 解決 = new Solver();
解決.solve(問題, m -> 答(変数, m));
}
@Test
void testWikipedia束縛順序指定なし() {
// Wikipedia 数独 の例題
// https://ja.wikipedia.org/wiki/%E6%95%B0%E7%8B%AC
int[][] 入力 = {
{ 5, 3, 0, 0, 7, 0, 0, 0, 0 },
{ 6, 0, 0, 1, 9, 5, 0, 0, 0 },
{ 0, 9, 8, 0, 0, 0, 0, 6, 0 },
{ 8, 0, 0, 0, 6, 0, 0, 0, 3 },
{ 4, 0, 0, 8, 0, 3, 0, 0, 1 },
{ 7, 0, 0, 0, 2, 0, 0, 0, 6 },
{ 0, 6, 0, 0, 0, 0, 2, 8, 0 },
{ 0, 0, 0, 4, 1, 9, 0, 0, 5 },
{ 0, 0, 0, 0, 8, 0, 0, 7, 9 },
};
logger.info("test wikipedia");
数独束縛順序指定なし(入力);
}
とりあえず解けましたが、20秒以上かかりました。
2020-05-16T21:01:31.789 情報 test wikipedia
2020-05-16T21:01:52.360 情報 5 3 4 6 7 8 9 1 2
2020-05-16T21:01:52.361 情報 6 7 2 1 9 5 3 4 8
2020-05-16T21:01:52.361 情報 1 9 8 3 4 2 5 6 7
2020-05-16T21:01:52.362 情報 8 5 9 7 6 1 4 2 3
2020-05-16T21:01:52.363 情報 4 2 6 8 5 3 7 9 1
2020-05-16T21:01:52.363 情報 7 1 3 9 2 4 8 5 6
2020-05-16T21:01:52.363 情報 9 6 1 5 3 7 2 8 4
2020-05-16T21:01:52.364 情報 2 8 7 4 1 9 6 3 5
2020-05-16T21:01:52.365 情報 3 4 5 2 8 6 1 7 9
変数の束縛順は単純に上から下、左から右なので、少し工夫してみます。
以下の方針で束縛順を定義します。
- 数字の決定しているマス目は先に束縛します。これらのマス目は値が決定しているの後戻りがありません。
- 行、列、3x3の領域ごとにみて、なるべく数字の決定しているマス目が多い所から順に束縛します。以下の図に示すように、青で示した領域は6個の値が確定しています。赤で示した4つの領域は5個の値が確定しています。青の領域に含まれる変数→赤の領域に含まれる変数→...の順に束縛します。
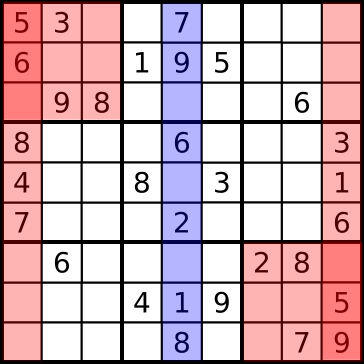
この方針に従って変数の束縛順を変えたものが以下のコードです。
static List<Variable> 束縛順序定義(List<Variable> 変数, List<Variable[]> 制約変数) {
Set<Variable> 束縛順序 = new LinkedHashSet<>();
for (Variable v : 変数)
if (v.domain.size() == 1)
束縛順序.add(v);
Collections.sort(制約変数,
Comparator.comparingInt(a -> Arrays.stream(a).mapToInt(v -> v.domain.size()).sum()));
for (Variable[] a : 制約変数)
for (Variable v : a)
束縛順序.add(v);
return new ArrayList<>(束縛順序);
}
static void 数独束縛順序指定あり(int[][] 入力) {
Problem 問題 = new Problem();
Variable[][] 変数 = 変数定義(問題, 入力);
List<Variable[]> 制約変数 = 制約定義(問題, 変数);
List<Variable> 束縛順序 = 束縛順序定義(問題.variables, 制約変数);
Solver 解決 = new Solver();
解決.solve(問題, 束縛順序, m -> 答(変数, m));
}
結果としては0.02秒程度で解けるようになりました。この例題は単純すぎるのでもっと難しい問題にチャレンジしてみました。Wikipediaによれば、数独の解が唯一になるためには数字の決まっているマス目が17個以上必要だそうです。
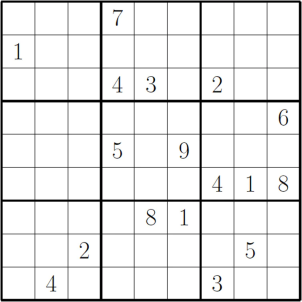
ネットで検索して数字の決まっているマス目が丁度17個の難しそうな問題を拾ってみました。
@Test
void testGood_at_Sudoku_Heres_some_youll_never_complete() {
// http://theconversation.com/good-at-sudoku-heres-some-youll-never-complete-5234
int[][] 入力 = {
{ 0, 0, 0, 7, 0, 0, 0, 0, 0 },
{ 1, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 4, 3, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 6 },
{ 0, 0, 0, 5, 0, 9, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 4, 1, 8 },
{ 0, 0, 0, 0, 8, 1, 0, 0, 0 },
{ 0, 0, 2, 0, 0, 0, 0, 5, 0 },
{ 0, 4, 0, 0, 0, 0, 3, 0, 0 },
};
logger.info("Good at Sudoku Heres some youll never complete");
数独束縛順序指定あり(入力);
}
1秒以内に解くことができました。
2020-05-16T21:22:26.176 情報 Good at Sudoku Heres some youll never complete
2020-05-16T21:22:26.310 情報 2 6 4 7 1 5 8 3 9
2020-05-16T21:22:26.311 情報 1 3 7 8 9 2 6 4 5
2020-05-16T21:22:26.312 情報 5 9 8 4 3 6 2 7 1
2020-05-16T21:22:26.313 情報 4 2 3 1 7 8 5 9 6
2020-05-16T21:22:26.315 情報 8 1 6 5 4 9 7 2 3
2020-05-16T21:22:26.316 情報 7 5 9 6 2 3 4 1 8
2020-05-16T21:22:26.317 情報 3 7 5 2 8 1 9 6 4
2020-05-16T21:22:26.318 情報 9 8 2 3 6 4 1 5 7
2020-05-16T21:22:26.320 情報 6 4 1 9 5 7 3 8 2
変数の束縛順序を指定しない場合は10分経っても解けませんでした。
制約表現の改善
制約を定義するときはラムダ式と関連する変数を指定します。制約の対象となる変数の数は可変なので、このような書き方になります。
problem.constraint(a ->
number(a[0], a[1], a[2], a[3])
+ number(a[4], a[5], a[6], a[1])
== number(a[4], a[5], a[2], a[1], a[7]),
S, E, N, D, M, O, R, Y);
a[0]がSに、a[1]がEに、...という対応関係にあるのですが、分かりにくい表現になっています。これを改善するために固定長引数のメソッドを追加します。まず最初に、以下のインタフェースを追加します。
@FunctionalInterface
public interface Predicate1 extends Predicate {
default boolean test(int... values) {
return test(values[0]);
}
boolean test(int a);
}
@FunctionalInterface
public interface Predicate2 extends Predicate {
default boolean test(int... values) {
return test(values[0], values[1]);
}
boolean test(int a, int b);
}
.....
次にProblemクラスにこれを使用した制約のファクトリメソッドを追加します。
public Constraint constraint(Predicate1 predicate, Variable a) {
return constraint((Predicate)predicate, a);
}
public Constraint constraint(Predicate2 predicate, Variable a, Variable b) {
return constraint((Predicate)predicate, a, b);
}
.....
そうすると、このような書き方ができるようになります。constraint()メソッドに渡すVariableの数とラムダ式の引数の数が一致しないとコンパイルエラーになります。
problem.constraint((s, e, n, d, m, o, r, y) ->
number(s, e, n, d)
+ number(m, o, r, e)
== number(m, o, n, e, y),
S, E, N, D, M, O, R, Y);
まとめ
性能に影響するのは以下の点であることがわかりました。
-
制約の与え方
制約を細かくして変数束縛の早い段階でチェックできるようにすると、選択肢が絞られるので速くなります。 -
変数束縛の順序
選択肢の少ない変数を先に束縛すると速くなります。