kurenaifさんにmuck-a-muckのwriteupを書いてもらうために自分もwriteupを書くことにしました.
DLP 4.0
import os
import secrets
import signal
FLAG = os.getenv("FLAG", "FAKEFLAG{THIS_IS_FAKE}")
if __name__ == "__main__":
signal.alarm(333)
p = int(input("What's your favorite 333-bit p: "))
if not is_prime(p) or p.bit_length() != 333:
print("Invalid p")
exit()
order = p**2 - 1
x = secrets.randbelow(order)
Q = QuaternionAlgebra(Zmod(p), -1, -1)
g = Q.random_element()
h = g**x
print(f"{g = }")
print(f"{h = }")
_x = int(input("Guess x: "))
if g**_x == h:
print(FLAG)
else:
print("NO FLAG")
四元数の離散対数問題です. $p$をこちらから指定できるので$\varphi(p)
$の素因数 Pohlig–Hellman algorithm を用いて離散対数問題を解くことができます.
というわけでまずそのような$333$bit素数を探してこないといけません
from Crypto.Util.number import getPrime, isPrime
t = 1
for i in range(10000):
p = Primes()
t *= p.unrank(i)
if len(bin(int(t + 1))[2:]) == 333 and isPrime(int(t + 1)):
print(t + 1)
print(len(bin(int(t + 1))))
break
elif len(bin(int(t))) > 333:
while len(bin(int(t))) > 333:
t //= getPrime(len(bin(int(t))[2:]) - 100)
else:
continue
print(factor(t))
solve1.sageで$p=16033419932502986469037291427850365121716627585835910890032900960816840045300923995323317366410694661$を得ました.
$\mod p$上の4元数に対して Pohlig–Hellman algorithm を適用せずにその絶対値の2乗に対して適用しました.
def fast_dlp_modn(H, G, n):
return int(pari(f"znlog({H}, Mod({G}, {n}))"))
g = [
10574785669437053346460855274101765079926527156435114060684936013444693474513418665386014039279892360,
11804743590594086793205518143144243933915696733500960553102945550815013856707501681266383662910190466,
7702563307652547444139815157687071577685298555987273908224271224559325002791811117802596224796655243,
13131661278034532409159200125836863854067784171016940507434161024540649930096249081912606216978083103,
]
h = [
12582425849478489067703813004513843030298821460495120678211987089170893681521733732769395491181812508,
71140667351304439771702228354606580027717957703387229390348649244481789665458974114357620201525437,
727887411434074784475642696372521753765894615469985853922104017787522324571701971915021832299619105,
11307198890461502314840521692749101049689436507205606042087217255209853340300627394877294102776519227,
]
# assert Q.order() == p**4
# assert g == g ** Q.order()
p = 16033419932502986469037291427850365121716627585835910890032900960816840045300923995323317366410694661
absg = int(g[0]) ** 2 + int(g[1]) ** 2 + int(g[2]) ** 2 + int(g[3]) ** 2
absh = int(h[0]) ** 2 + int(h[1]) ** 2 + int(h[2]) ** 2 + int(h[3]) ** 2
# assert Mod(absg, p) ** x == Mod(absh, p)
g = Mod(absg, p)
y = Mod(absh, p)
phi_p = "2 * 3 * 7 * 281 * 585131 * 2283091 * 66558319 * 38812459031 * 8407411055293 * 8899182573469"
x = fast_dlp_modn(y, g, p)
print("[+] x:", x)
KEX 4.0
import os
from hashlib import sha256
from secrets import randbelow
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
FLAG = os.getenvb(b"FLAG", b"FAKEFLAG{THIS_IS_FAKE}")
p = 0xC20C8EDB31BFFA707DC377C2A22BE4492D1F8399FFFD388051EC5E4B68B4598B
order = p**2 - 1
Q = QuaternionAlgebra(Zmod(p), -1, -1)
i, j, k = Q.gens()
pub_A = (
71415146914196662946266805639224515745292845736145778437699059682221311130458
+ 62701913347890051538907814870965077916111721435130899071333272292377551546304 * i
+ 60374783698776725786512193196748274323404201992828981498782975421278885827246 * j
+ 60410367194208847852312272987063897634106232443697621355781061985831882747944 * k
)
pub_B = (
57454549555647442495706111545554537469908616677114191664810647665039190180615
+ 8463288093684346104394651092611097313600237307653573145032139257020916133199 * i
+ 38959331790836590587805534615513493167925052251948090437650728000899924590900 * j
+ 62208987621778633113508589266272290155044608391260407785963749700479202930623 * k
)
def hash_Q(x):
return sha256(
long_to_bytes(int(x[0]))
+ long_to_bytes(int(x[1]))
+ long_to_bytes(int(x[2]))
+ long_to_bytes(int(x[3]))
).digest()
if __name__ == "__main__":
# Alice sends share_A to Bob
priv_A = randbelow(order)
A = pub_A**priv_A
share_A = A**-1 * pub_B * A
print(f"{share_A = }")
# Bob sends share_B to Alice
priv_B = randbelow(order)
B = pub_B**priv_B
share_B = B**-1 * pub_A * B
print(f"{share_B = }")
# Alice computes the shared key
Ka = A**-1 * share_B**priv_A
# Bob computes the shared key
Kb = share_A**-priv_B * B
assert Ka == Kb
# Encrypt FLAG with the shared key
key = hash_Q(Ka)
cipher = AES.new(key, mode=AES.MODE_CTR)
nonce = cipher.nonce.hex()
enc = cipher.encrypt(FLAG).hex()
print(f"{nonce = }")
print(f"{enc = }")
四元数上の Diffie–Hellman 鍵交換です. コードからわかる情報を羅列していきます.
- $\mathrm{Ka}=\mathrm{Kb}=A^{-1}B^{-1}AB$
- $A=A_{pub}^a$, $B=B_{pub}^b$
- $A_{share}=A^{-1}B_{pub}A$, $B_{share}=B^{-1}A_{pub}B$
四元数の行列は対角化できます. (SECCON2023 QualsのRSA4.0の作問者writeupの想定解法でも用いられています).
私の場合は$4\times4$の行列でやりました
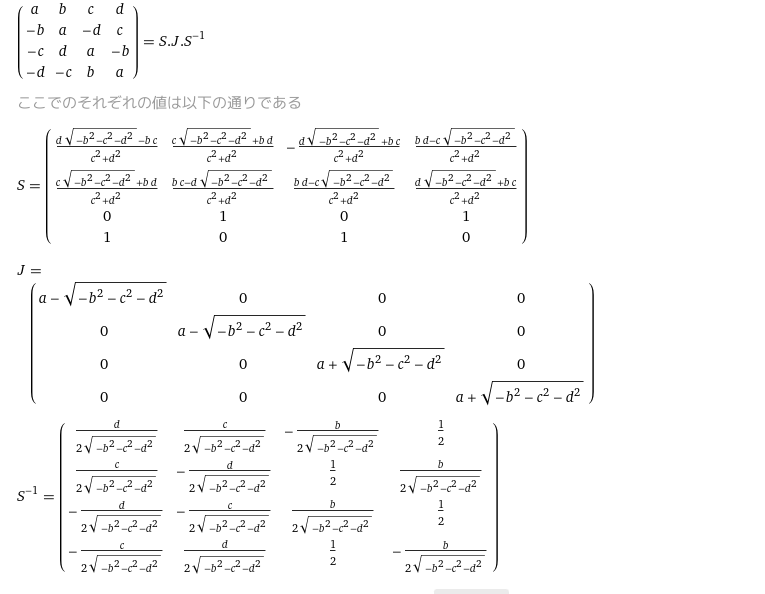
\begin{aligned}
A_{pub}&= P_AD_AP_A^{-1}\\
B_{pub}&=P_BD_BP_B^{-1}\\
A&=P_AD_A^aP_A^{-1}\\
B&=P_BD_B^bP_B^{-1}
\end{aligned}
より
\begin{aligned}
P_A^{-1}A_{share}P_A&=D_A^{-a}(P_A^{-1}B_{pub}P_A)D_A^a\\
P_B^{-1}B_{share}P_B&=D_B^{-b}(P_B^{-1}B_{pub}P_B)D_B^b
\end{aligned}
$P_A^{-1}B_{pub}P_A$, $P_B^{-1}B_{pub}P_B$は既知の情報から求めることが可能です.
$D_A^a, D_B^b$は対角行列です.
D^{-1}TD=
\begin{pmatrix}
\frac{1}{x} & 0 & 0 & 0\\
0 & \frac{1}{x} & 0 & 0\\
0 & 0& \frac{1}{y} & 0 \\
0 & 0 & 0 & \frac{1}{y}\\
\end{pmatrix}
\begin{pmatrix}
a & b & c & d\\
e & f & g & h\\
i & j& k & l \\
m & n & o & p\\
\end{pmatrix}
\begin{pmatrix}
x & 0 & 0 & 0\\
0 & x & 0 & 0\\
0 & 0& y & 0 \\
0 & 0 & 0 & y\\
\end{pmatrix}
=
\begin{pmatrix}
a & \frac{by}{x} &\frac{cz}{x} & \frac{dw}{x}\\
\frac{ex}{y} & f & \frac{gz}{y} & \frac{hw}{y}\\
\frac{ix}{z} & \frac{jy}{z}& k & \frac{lw}{z} \\
\frac{mx}{w} & \frac{ny}{w} & \frac{oz}{w} & p\\
\end{pmatrix}
$D$には$D_A^a$又は$D_B^b$, $T$には$P_A^{-1}B_{pub}P_A$または$P_B^{-1}B_{pub}P_B$が入ります.
よって$x:y:w:z$を求めることができます. ($x:y=1:1$は求めまでもありませんがそれに気づいたのはコードを書き終わってからでした...)
そうして求めたものを$D_A'^{a}$と$D_B'^b$としてます. $D_A'^{a}$と$D_B'^b$はそれぞれある定数$k_A,k_B\in \mathbb{Z}/p\mathbb{Z}$を用いて
\begin{aligned}
D_A'^a&=k_AD_A^a\\
D_B'^b&=k_BD_B^b
\end{aligned}
の関係が成り立ちます. 一見この$k_A,k_B$を求める必要がありそうですがほしいものは $A^{-1}B^{-1}AB$なのでこのような定数は打ち消しあって影響を及ぼしません.
以下がそれらをもとに書かれたコードです. この問題は徹夜して解いたのでproblem.sageの上から追記する限界コーディングをしてます. またsageで有限体の拡大をどうやるかわからず行列計算を分割してやる羽目になってます...(わかる方, 教えていただけると幸いです.)
import os
from hashlib import sha256
from secrets import randbelow
from Crypto.Cipher import AES
from Crypto.Util.number import long_to_bytes
FLAG = os.getenvb(b"FLAG", b"FAKEFLAG{THIS_IS_FAKE}")
p = 0xC20C8EDB31BFFA707DC377C2A22BE4492D1F8399FFFD388051EC5E4B68B4598B
order = p**2 - 1
Q = QuaternionAlgebra(Zmod(p), -1, -1)
i, j, k = Q.gens()
pub_A = (
71415146914196662946266805639224515745292845736145778437699059682221311130458
+ 62701913347890051538907814870965077916111721435130899071333272292377551546304 * i
+ 60374783698776725786512193196748274323404201992828981498782975421278885827246 * j
+ 60410367194208847852312272987063897634106232443697621355781061985831882747944 * k
)
pub_B = (
57454549555647442495706111545554537469908616677114191664810647665039190180615
+ 8463288093684346104394651092611097313600237307653573145032139257020916133199 * i
+ 38959331790836590587805534615513493167925052251948090437650728000899924590900 * j
+ 62208987621778633113508589266272290155044608391260407785963749700479202930623 * k
)
def hash_Q(x):
return sha256(long_to_bytes(int(x[0])) + long_to_bytes(int(x[1])) + long_to_bytes(int(x[2])) + long_to_bytes(int(x[3]))).digest()
# diagonal matrix
def diag(m, p):
a = Mod(m[0][0], p)
b = Mod(m[0][1], p)
c = Mod(m[0][2], p)
d = Mod(m[0][3], p)
r = (-b ^ 2 - c ^ 2 - d ^ 2).square_root()
half = Mod(1, p) / Mod(2, p)
J = [
[a - r, 0, 0, 0],
[0, a - r, 0, 0],
[0, 0, a + r, 0],
[0, 0, 0, a + r],
]
S = [
[
(d * r - b * c) / (c ^ 2 + d ^ 2),
(c * r + b * d) / (c ^ 2 + d ^ 2),
-(d * r + b * c) / (c ^ 2 + d ^ 2),
(-c * r + b * d) / (c ^ 2 + d ^ 2),
],
[
(c * r + b * d) / (c ^ 2 + d ^ 2),
(-d * r + b * c) / (c ^ 2 + d ^ 2),
(-c * r + b * d) / (c ^ 2 + d ^ 2),
(d * r + b * c) / (c ^ 2 + d ^ 2),
],
[0, 1, 0, 1],
[1, 0, 1, 0],
]
Sinv = [
[
d / (2 * r),
c / (2 * r),
-b / (2 * r),
half,
],
[
c / (2 * r),
-d / (2 * r),
half,
b / (2 * r),
],
[
-d / (2 * r),
-c / (2 * r),
b / (2 * r),
half,
],
[
-c / (2 * r),
d / (2 * r),
half,
-b / (2 * r),
],
]
S = Matrix(S)
Sinv = Matrix(Sinv)
J = Matrix(J)
# print(Sinv * S)
# print(J)
# print(m.eigenmatrix_right())
assert S**-1 == Sinv
assert S * J * S**-1 == m
return S, J, Sinv
def divide_expression(expression):
# Find the position of the '+'
plus_index = expression.find("+")
# Extract the two parts of the expression
part1 = expression[:plus_index].strip()
part2 = expression[plus_index + 1 :].strip()
return part1, part2
def get_sqrt(expression):
e = divide_expression(expression)
t_index = e[0].find("t")
return e[0][t_index + 1 :].strip()
def to_mod(m):
new_m = [[0 for _ in range(4)] for _ in range(4)]
for i in range(4):
for j in range(4):
new_m[i][j] = Mod(int(m[i][j]), p)
new_m = Matrix(new_m)
return new_m
if __name__ == "__main__":
share_A = (
57454549555647442495706111545554537469908616677114191664810647665039190180615
+ 29676674584636622512615278554619783662266316745243745754583020553342447549066 * i
+ 13738434026348321269316223833101191512670504554293346482813342673413295266974 * j
+ 23943604179074440949144139144245518129342426692024663551007842394683089455212 * k
)
share_B = (
71415146914196662946266805639224515745292845736145778437699059682221311130458
+ 65071948237600563018819399020079518439338035815171479183947570522190990857574 * i
+ 52272525531848677372993318721896591307730532037121185733047803928301284987593 * j
+ 68406537373378314867132842983264676792172029888604057526079501977599097329576 * k
)
Pb, Tb, Pbinv = diag(pub_B.matrix(), p)
Pa, Ta, Painv = diag(pub_A.matrix(), p)
tmp = Painv * share_A.matrix() * Pa
assert Pb * Tb * Pbinv == pub_B.matrix()
mid = Painv * pub_B.matrix() * Pa
z_coff = tmp[0][2] / mid[0][2]
w_coff = tmp[0][3] / mid[0][3]
y_coff = (tmp[1][2] / z_coff / mid[1][2]) ** -1
PA_coff = (
Pa
* Matrix(
[
[1, 0, 0, 0],
[0, y_coff, 0, 0],
[0, 0, z_coff, 0],
[0, 0, 0, w_coff],
]
)
* Painv
)
tmpB = Pbinv * share_B.matrix() * Pb
midB = Pbinv * pub_A.matrix() * Pb
z_coffB = tmpB[0][2] / midB[0][2]
w_coffB = tmpB[0][3] / midB[0][3]
y_coffB = (tmpB[1][2] / z_coffB / midB[1][2]) ** -1
PB_coff = (
Pb
* Matrix(
[
[1 / w_coffB, 0, 0, 0],
[0, y_coffB / w_coffB, 0, 0],
[0, 0, z_coffB / w_coffB, 0],
[0, 0, 0, w_coffB / w_coffB],
]
)
* Pbinv
)
real_PA_coff = [[0 for _ in range(4)] for _ in range(4)]
real_PB_coff = [[0 for _ in range(4)] for _ in range(4)]
real_PAinv_coff = [[0 for _ in range(4)] for _ in range(4)]
real_PBinv_coff = [[0 for _ in range(4)] for _ in range(4)]
for i in range(4):
for j in range(4):
real_PA_coff[i][j] = Mod(int(divide_expression(str(PA_coff[i][j]))[1]), p)
real_PB_coff[i][j] = Mod(int(divide_expression(str(PB_coff[i][j]))[1]), p)
real_PAinv_coff[i][j] = Mod(int(divide_expression(str((PA_coff**-1)[i][j]))[1]), p)
real_PBinv_coff[i][j] = Mod(int(divide_expression(str((PB_coff**-1)[i][j]))[1]), p)
real_PA_coff = Matrix(real_PA_coff)
real_PB_coff = Matrix(real_PB_coff)
real_PAinv_coff = Matrix(real_PAinv_coff)
real_PBinv_coff = Matrix(real_PBinv_coff)
sa = Mod(int(get_sqrt(str(PA_coff[0][0]))), p)
sb = Mod(int(get_sqrt(str(PB_coff[0][0]))), p)
both_sqrt = (sa * sb).sqrt()
real_AB = (
to_mod(real_PA_coff) * to_mod(real_PB_coff)
+ to_mod((PA_coff - real_PA_coff) / sa.sqrt()) * to_mod((PB_coff - real_PB_coff) / sb.sqrt()) * both_sqrt
)
im_AB = []
im_AB.append(to_mod((PA_coff - real_PA_coff) * (real_PB_coff) / sa.sqrt()))
im_AB.append(to_mod((real_PA_coff * (PB_coff - real_PB_coff)) / sb.sqrt()))
real_ABinv = (
real_PAinv_coff * real_PBinv_coff
+ to_mod((PA_coff**-1 - real_PAinv_coff) / sa.sqrt()) * to_mod((PB_coff**-1 - real_PBinv_coff) / sb.sqrt()) * both_sqrt
)
im_AB_inv = []
im_AB_inv.append(to_mod(((PA_coff**-1 - real_PAinv_coff) * real_PBinv_coff) / sa.sqrt()))
im_AB_inv.append(to_mod((real_PAinv_coff * (PB_coff**-1 - real_PBinv_coff)) / sb.sqrt()))
real = (
real_ABinv * real_AB
+ im_AB_inv[0] * im_AB[0] * sa
+ im_AB_inv[1] * im_AB[1] * sb
+ (im_AB_inv[1] * im_AB[0] + im_AB_inv[0] * im_AB[1]) * both_sqrt
)
key = hash_Q(real[0])
nonce = long_to_bytes(0x6CED0927695BC45E)
cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
nonce = cipher.nonce.hex()
enc = long_to_bytes(
0x6A59A899FED260513CD4AD037BB3D8681AE47E4D5C13139AEBDE981C01F93AAC63D6A39C04E4DFA3FD05FA41C1BCDA8B39C660AFF5673458D5324EAC738D1BD0A255
)
plain = cipher.decrypt(enc)
print(plain)
muck-a-muck
何もわからず会場でチャチャチャを踊りながら椅子を暖めてました.
kurenaifさんWriteup待ってます()
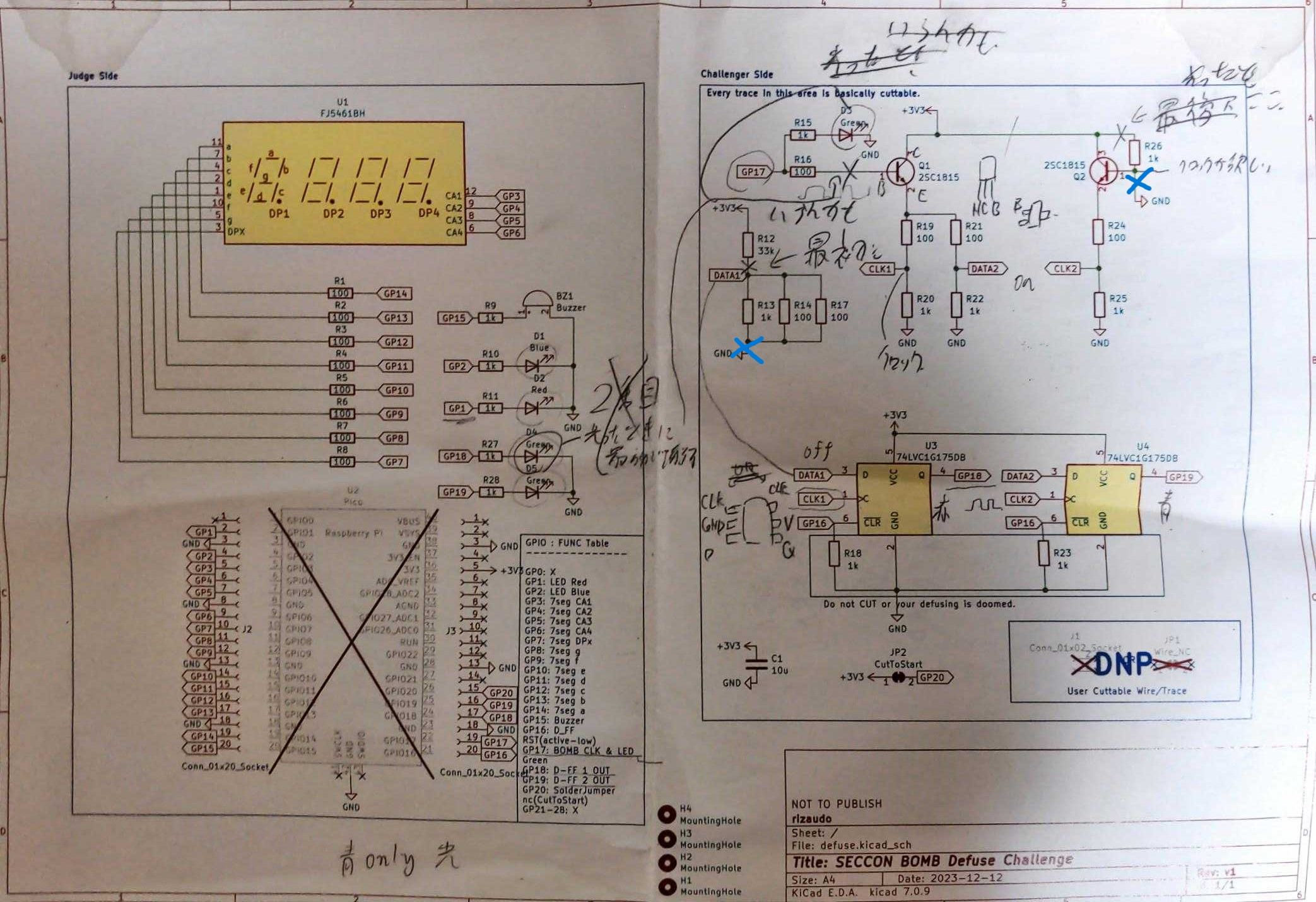
ハードウェア問
戦犯をしました. 問題名は分からないです.
正しい解法は水色の部分を切断することです.
トランジスタがGNDに張り付いているのでU_4のD_FFの出力が0なのでタイミングを計って切断することと, DATA1も分圧のせいでU_3のD_FFの出力が0なので切断して1が出力されるようにします. R14, R17 だけをきればよいらしいですが$3.3/34\sim0.097\mathrm{V}$だとやはり電圧が低すぎる気がする...
upsolveしたいですがダウンロードしていなくてコードをコードが手元にないので(は?)今すべてを保存していたチームメンバに送ってもらってます. 届いたらやります. 届きましたが眠いので明日やります...