はじめに
本投稿ではサンクトペテルブルクのパラドックスについての私の考察を記事にする。まず最初にパラドックスの内容を確認しておこう。
パラドックスの内容
サンクトペテルブルクのパラドックスのwikiより
偏りのないコインを表が出るまで投げ続け、表が出たときに賞金をもらえるゲームがあるとする。もらえる賞金は、1回目に表が出たら1円、1回目は裏が出て2回目に表が出たら倍の2円、2回目まで裏が出ていて3回目に初めて表が出たらそのまた倍の4円、3回目まで裏が出ていて4回目に初めて表が出たらそのまた倍の8円、というふうに倍々で増える賞金がもらえるというゲームである。
つまり表が初めて出るまでに投げた回数を n とすると、2n−1 円もらえるのである。10回目に初めて表が出れば512円、20回目に初めて表が出れば52万4288円、30回目に初めて表が出れば5億3687万0912円がもらえる。ここで、このゲームには参加費(=賭け金)が必要であるとしたら、参加費の金額が何円までなら払っても損ではないと言えるだろうか。
数学的にはこの種の問題では、賞金の期待値を算出し参加費がその期待値以下であれば参加者は損しないと判断する。しかし、この問題における賞金の期待値を計算してみると、その数値は無限大に発散してしまうのである。すなわち期待値を W とすると、
$$
W=\sum _{k=1}^{\infty }\left({\frac {1}{2^{k}}}\cdot 2^{k-1}\right)={\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty
$$
となる。したがって、期待値によって判断するならば、参加費(=賭け金)がいくら大金であっても参加すべきであると結論になる。ところが実際には、このゲームでは 1/2 の確率で1円、1/4 の確率で2円、1/1024 の確率で512円の賞金が得られるに過ぎない(賞金が512円以下にとどまる確率が1023/1024)。したがって、そんなに得であるはずがないことは直観的に分かる。これが、この問題がパラドックスとされる所以である。
私の結論
引用しながら私の結論を最初に整理しておく。
したがって、期待値によって判断するならば、参加費(=賭け金)がいくら大金であっても参加すべきであると結論になる。
期待値によって判断するのであれば、間違いなくいくら大金であっても参加側の期待値が+になる賭けと言えるだろう。ただし、参加すべきかは別の話である。
そんなに得であるはずがないことは直観的に分かる。
なぜ、期待値は確実に+になるのに直観的には損だと思うのだろうか?これは、参加者の財産が胴元と比べて極端に少ない場合に起こる現象であると言える。これをわかりやすく理解するために、wikiの途中にある胴元の支払い能力から上限を設定すると妥当な金額が求まるというのを使う。ここで胴元の支払い能力の上限を $2^{999999998}$円 と設定する。すると、期待値は 5億円 となるため、期待値によって判断するのであれば、間違いなく 5億円 以下であれば参加すべきであるとなるだろう。しかし、期待値がしっかり求まっても直観的にこの賭けに参加すべきではないと思うはずだ。私の直観で申し訳ないが、私がこの賭けに参加しない理由を例にすると「5億あれば遊んで暮らせるのに、それを失ってまでより大金を得る必要が無い」からである。
これが、この問題がパラドックスとされる所以である。
では最後にこのパラドックスを解決していこう。先ほどの胴元の支払い能力の上限を $2^{999999998}$円 と設定した例のように、このパラドックスは上限が無限だからとかは一切関係なく、上限が決まっていても起こる現象である。そこで私は、「参加すべき妥当な掛け金は?」という視点ではなく、「期待値で胴元と参加者が対等に賭けを行うには?」という視点で考えてみる。そうして考えると、参加者の支払い能力も胴元と同じ $2^{999999998}$円 と設定してみればよいのではないかと結論付ける。すると、$2^{999999998}$円 に対して期待値の 5億円 は微々たる金額であるため、特におかしい賭けには感じず対等に遊ぶことができるであろう。
さて、後はこの上限をどんどん上げていけば無限となりサンクトペテルブルクのパラドックスと一致する。したがって、胴元が無限の支払い能力を持つと仮定するのであれば、この賭けの期待値は無限で間違いなくこれが対等な掛け金で問題ないだろう。ただし、これを対等な賭けと認識するには、参加する側も胴元と等しいだけの無限の支払い能力(無限の掛け金を無限回支払うことができる)を持つ必要がある。と私は結論付ける。
これをさらに直観的にわかりやすくするため、$2^{999999998}$円 を100万ペリカとして、それに合わせて掛け金の方をスケーリングしてみよう。つまり値としては $10^6/2^{999999998}$ になったので、掛け金のスタートを$5×10^{14}/2^{999999998}$ペリカ にすればよいでしょう。すごく雑に見やすくして $5×10^{-2999999992}$ペリカ くらいですかね? これで大分見やすくなって, 掛け金5億円は総資産100万ペリカのうち、$5×10^{-2999999992}$ペリカ程度なので、胴元や参加者からするとすごく安いことがわかりますね。
wiki内のその他の意見
最後に、wiki内には「現実的な回答」「効用による回答」「反響」「標本抽出による解答」「発展的話題」について触れておく。
現実的な回答
これについては、対等に遊ぶために上限を設定する時に用いるアイディアであろう。したがって、胴元の支払い能力 or 参加者の支払い能力から上限を設定し、期待値を求めて遊べばよい。
効用による回答
胴元の支払い能力に上限がある場合で掛け金が期待値以下であっても、自分の支払い能力によっては直観的に参加すべきではないという話はした。その直観を裏付ける方法として、期待値ではなく自身の支払い能力から「効用」の視点で参加するかしないかの判断をする際に用いるアイディアであろう。
反響
これは明らかに間違っている。掛け金の期待値は回数に依存しないし、回数によって公平性が変化することはない。そもそも、胴元の支払い能力の上限を $2^{999999998}$円 と設定した場合の期待値が 5億円 なのでそれ以下の掛け金を設定するのは容易に対等ではないと結論付けられる。
標本抽出による解答
これは傾向としてそうなるが、そこから対等な掛け金には結びつくことはない。なぜ傾向としてそうなるかというと、試行回数が増えるにしたがって期待値に近づきやすくなるからであり、単にそれだけである。これについては膨大な数の玉(100兆とか?)にあたり玉を1つが入っているガラガラとかを用意し(玉は再利用式)、あたり玉が出たときに賞金がもらえる!みたいなのでも同じことが起こるので試して見るといいだろう。
発展的話題
まとめ売りしても変わりません。また、先の例で胴元の支払い能力に上限を設けた際の期待値が5億円だったので、5億円以下はの結論を出す議論は全て間違いだと言えます。
どうして勘違いが起こる?
私は「反響」「標本抽出による解答」「発展的話題」については明らかに間違いであり、考察者の勘違いだと思っています。ではなぜこの勘違いが起こるのかを色々調べつつ、pythonでコードを組みつつ実験してみました。
現象近似の罠
例えば標本抽出で勘違いしている例として、以下のように参加回数に応じて、確率から現象が起こる回数を近似して考えるというのがありました。小さい確率は無視してしまいましょう!という奴ですね。
import pandas as pd
df = pd.DataFrame()
df['回数'] = np.arange(25)
df['賞金'] = 2**df['回数']
df['確率'] = 1/2**df['回数']
df['10回'] = (df['確率'] * 10).astype('i')
df['100回'] = (df['確率'] * 100).astype('i')
df['1000回'] = (df['確率'] * 1000).astype('i')
df['10000回'] = (df['確率'] * 10000).astype('i')
df['100000回'] = (df['確率'] * 100000).astype('i')
df
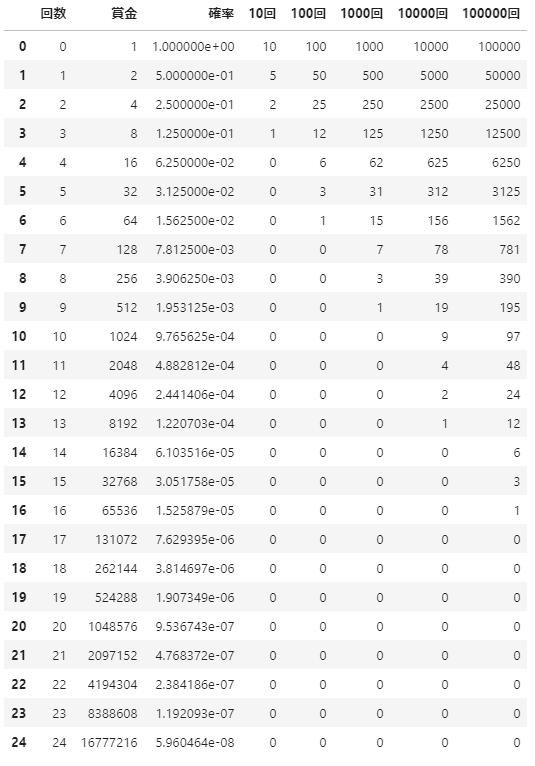
すると以下のような表が出来上がってしまいます。
この表からグラフを作ってしまうと…
res = []
N = [10 * 10**i for i in range(5)]
for n in N:
res.append(np.sum(df[str(n)+'回'] * df['賞金']) / np.sum(df[str(n)+'回']))
plt.plot(N, res)
試行回数によって期待値が変動するように見え、「これは試行回数によって期待値が変わる!」みたいに勘違いしてしまいます。実際には現象が起こる確率を「近似」した際に、実際の現象と差が生まれ、その差が期待値に与える影響があまりにも大きいためこのようなことが起こります。
ガラガラでやってみた
ではこれを上で少し話したガラガラでやってみましょう!条件は、あたる確率が1億分の1のガラガラで賞金は3億円、一度出た玉も再利用すると仮定します。同じようにやってみると?
df = pd.DataFrame()
df['賞金'] = [0, 300000000]
df['確率'] = [1 - 1/100000000, 1/100000000]
N = [10 * 10**i for i in range(8)]
res = []
for n in N:
df[str(n)+'回'] = (df['確率'] * n).astype('i')
res.append(np.sum(df[str(n)+'回'] * df['賞金']) / np.sum(df[str(n)+'回']))
plt.plot(res)
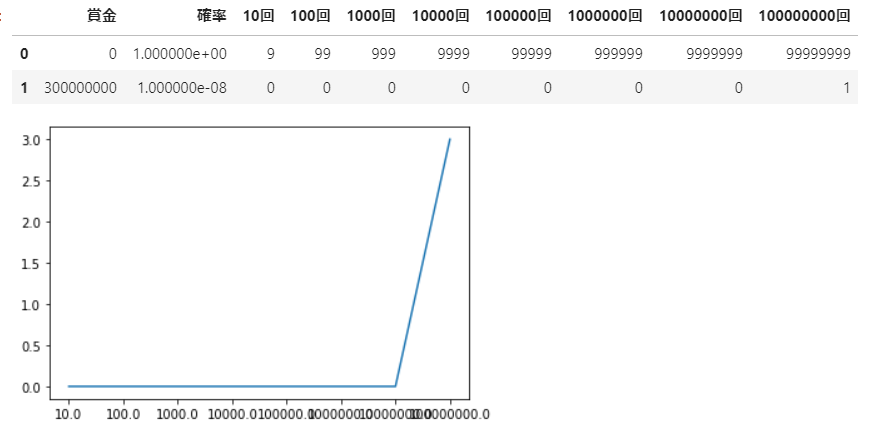
df
こんな感じになります。こうするとわかりやすいですね!先ほどの現象の近似が正しく、それによって期待値が決まるとすると…「このガラガラは1000回しかやらないんだからタダでやらせろ!」みたいな無茶苦茶になってしまいます。