Python: ウェーブレット変換の実装：①Ricker Waveletの実装編

はじめに

背景

私的に超解釈するとウェーブレット変換は
「基本となる波(Mother wave)のサイズや位置を変化させながら足し合わせることで元となる波形を表現する」
ってことっぽい？

以下はscipyに実装されているウェーブレット変換を参考に作成中のcwt関数である.（作りかけ）

def cwt(d, mw, wid):
    y = np.zeros([len(wid), len(d)])
    for i, j in enumerate(wid):
        wave = mw(min(10 * j, len(d)), j)
        y[i, :] = np.convolve(d, wave, mode='same')
    return y

少し補足すると, 以下の部分でサイズ感jに応じたMother waveを作って

wave = mw(min(10 * j, len(d)), j)

以下でその波形の位置をずらしながら畳み込んでいる

y[i, :] = np.convolve(d, wave, mode='same')

課題と目標

課題

作成したcft関数は引数mwにscipy.signal.rickerなど用意されたものを渡し動作するのが現状である.
このscipy.signal.rickerは, 基本となる波によく用いられるRicker Waveletのことである. 参考wiki⇒wiki

目標

したがって, 本投稿の目標は一つ目のMother WaveとしてRicker Waveletを実装することである.

Ricker Wavelet

前振りが長く壮大に何か始まりそうだが, Ricker Waveletはしょせん以下の式でサクッともとまる.

${\LARGE\psi (t)={\frac {2}{{\sqrt {3\sigma }}\pi ^{1/4}}}\left(1-\left({\frac {t}{\sigma }}\right)^{2}\right)e^{-{\frac {t^{2}}{2\sigma ^{2}}}}}$

ここでσはサイズ感を変更するようなパラメータなので実行時に引数で適当に与えられるようにすればよい.
てことで実装すると以下のようになる.

signal.py

import numpy as np

def ricker(t, s=1.0):
    a = 2 * np.sqrt(3 * s) * np.pi**0.25
    b = 1 - (t / s)**2
    c = np.e**(-1 * t**2 / (2 * s**2))
    return a * b * c

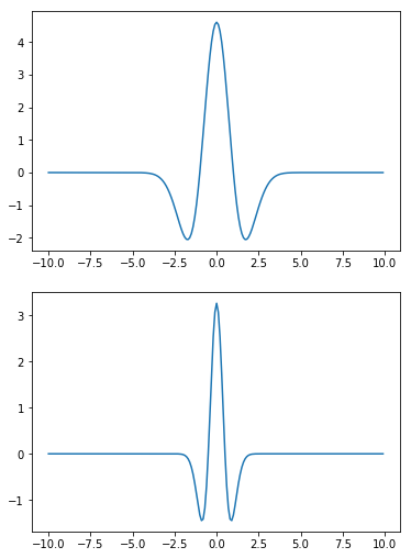
実際につかって波形を見てみる. 今回はσ=1.0(デフォルト値)とσ=0.5で生成した.

%matplotlib inline
import matplotlib.pyplot as plt

import numpy as np

# ステップ
s = 0.1
# 横軸(-10~10まで)
x = np.arange(-10, 10, s)
y1 = ricker(x)
plt.plot(x, y1)
plt.show()
y2 = ricker(x, 0.5)
plt.plot(x, y2)
plt.show()

実行結果は以下の通り.wikiにある波形が生成されている. wiki
また,σによってサイズ感がかわってることも確認できる.

パラメータ設定方法の変更

scipy.signal.rickerの引数がwidとαなので, xをwidとαで作成する形式でs_ricker関数を作成した.
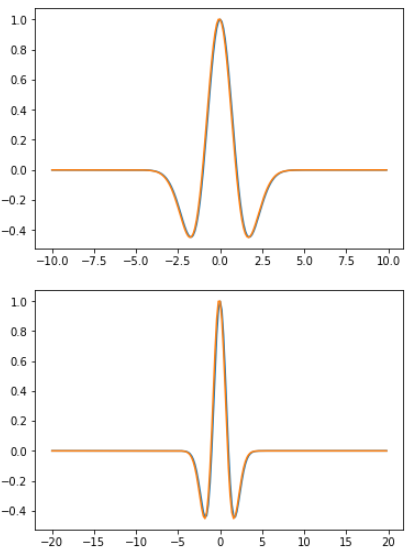
作成した関数とscipy.signal.rickerを比較してみるとほぼほぼ同じ波形が得られた.
※振幅が違ったので全ての波形で最大が1になるように変換している.

%matplotlib inline
import matplotlib.pyplot as plt

import numpy as np
from scipy import signal

def s_ricker(wid, a):
    x = (np.arange(wid) - int(wid / 2)) / a
    return ricker(x)

wid = 200
a = 10
# 横軸(-1~1までの200個配列)
x = (np.arange(wid) - int(wid / 2)) / a
y1 = s_ricker(wid, a)
y2 = signal.ricker(wid, a)
plt.plot(x, y1 / np.max(y1))
plt.plot(x, y2 / np.max(y2))
plt.show()
a = 5
# 横軸(-1~1までの200個配列)
x = (np.arange(wid) - int(wid / 2)) / a
y1 = s_ricker(wid, a)
y2 = signal.ricker(wid, a)
plt.plot(x, y1 / np.max(y1))
plt.plot(x, y2 / np.max(y2))
plt.show()

実行結果
ほぼ一致（少しわかりにくいが, 橙の線の裏に青い線が重なっている）

実験

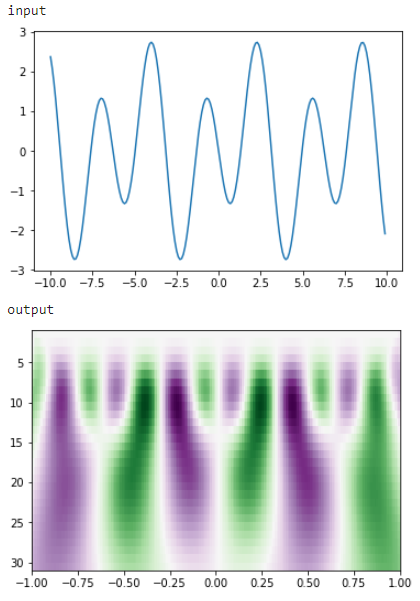
ここまでの全体をまとめ, 背景部分で紹介したcftで変換してみたのでその実行結果を紹介する.
（まだ色々調整が必要そうなのでそこはおいおい）

%matplotlib inline

import math

import matplotlib.pyplot as plt
import numpy as np


def ricker(t, s=1.0):
    a = 2 * np.sqrt(3 * s) * np.pi**0.25
    b = 1 - (t / s)**2
    c = np.e**(-1 * t**2 / (2 * s**2))
    return a * b * c


def s_ricker(wid, a):
    x = (np.arange(wid) - int(wid / 2)) / a
    return ricker(x)


def cwt(d, mw, wid):
    y = np.zeros([len(wid), len(d)])
    for i, j in enumerate(wid):
        wave = mw(min(10 * j, len(d)), j)
        y[i, :] = np.convolve(d, wave, mode='same')
    return y


s = 0.1
x = np.arange(-10, 10, s)
X = x.reshape(1, -1)
O = np.array([1, 2]).reshape(-1, 1)
B = np.array([0, math.pi]).reshape(-1, 1)
A = np.array([1, 2]).reshape(-1, 1)
y = np.sum(A * np.sin(O * X + B), axis=0)
print('input')
plt.plot(x, y)
plt.show()

widths = np.arange(1, 31)
cy = cwt(y, s_ricker, widths)
print('output')
plt.imshow(cy, extent=[-1, 1, 31, 1], cmap='PRGn', aspect='auto',
           vmax=abs(cy).max(), vmin=-abs(cy).max())
plt.show()

まとめ

Ricker Waveletを実装し, お試し段階だがCWTによる変換まで実現できた.
今後はCFTの変換部分を中心に見ていき, 分かった内容をまとめていきたい.

感想

こっちは専門ではなかったがなんとなくウェーブレット変換についてわかってきた.
理解した内容を専門のDeep Learningでも生かせるといいなぁ(´・ω・｀)