なにこれ
定常状態のシュレーディンガー方程式
$$
H\psi = E\psi
$$
を行列の固有値を求める方法で解いて可視化しました。
N番煎じくらいの記事ですがご容赦ください。
数学
最低限だけメモしておきます。
波動関数のベクトル化
$N+ 1$個の$x$座標を取ります。一番小さいところを$x_0$とし、 $\Delta x$ごとに等間隔に切っていき、$x_i = x_0 + i\Delta x$($i = 0, 1, \cdots, N$)とします。その$x_i$での波動関数の値を$\psi_i = \psi(x_i)$と書きます。
すると、波動関数は
$$
\psi(x) = \left( \psi_0, \psi_1, \psi_2, \cdots, \psi_N \right)^\mathrm{T}
$$
というベクトルとして表現できます。
すると、微分などの関数に対する操作が行列として表現できます。
微分演算子
二回微分を行列の形にします。
D = \frac{1}{\Delta x^2}\left(\begin{matrix}
-2 & 1 & 0 & & \cdots& \\
1 & -2 & 1 & & 0 & \\
0 & 1 & -2 & & \cdots& \\
& \cdots & & -2 & 1 & 0 \\
& 0 & & 1 & -2 & 1 \\
& \cdots & & 0 & 1 & -2
\end{matrix}\right)
ポテンシャル
U = \left(\begin{matrix}
U(x_0) & 0 & 0 & & \cdots& \\
0 & U(x_1) & 0 & & 0 & \\
0 & 0 & U(x_2) & & \cdots& \\
& \cdots & & U(x_{N-2}) & 0 & 0 \\
& 0 & & 0 & U(x_{N-1}) & 0 \\
& \cdots & & 0 & 0 & U(x_N)
\end{matrix}\right)
対角成分に各$x_i$でのポテンシャルの値を並べただけです。
シュレーディンガー方程式
$\hbar = 1$としています。
H\psi = \left(-\frac{1}{2m}D + U \right)\psi = E\psi
ここまで来ると$H$が行列の形で具体的に書けることが分かると思います。すると適当な数値計算ライブラリを使って固有値を計算し、波動関数とエネルギーを求めることができます。
実装
ライブラリ
import numpy as np
import matplotlib.pyplot as plt
x軸の目盛り
max_x = 3.0
N = 400 + 1
dx = max_x*2/(N - 1)
x = np.arange(-max_x, max_x + dx*0.5, dx)
ポテンシャル面
x0m = -2.0
x0p = 2.0
U = 0.25*(x - x0m)**2*(x - x0p)**2
$\frac{1}{4}\left(x - 2\right)^2\left(x + 2\right)^2$ という4次式です。$x = \pm 2$ で最小値 $0$ を取り、$x = 0$で極大値をとります。グラフを書いてみたら分かりますが、この極大値がエネルギー障壁となっています。
微分演算子
D = np.eye(N, k=1)
D += -1 * np.eye(N)
D += D.T
D = D/(dx**2)
numpyの単位行列を作る関数eyeを駆使します。kに整数を渡すと対角線からずれたところに並べてくれます。
ハミルトニアン
m = 200.0
H = - D/(2.0*m) + np.diag(U)
固有値と固有ベクトルを求める
W, V = np.linalg.eigh(H)
Wが固有値が並んだベクトル、Vが固有ベクトルが並んだ行列になります。
グラフ描写準備
max_U = np.max(U)
min_e = min(np.min(W), np.min(U))
max_e = min(np.max(W), max_U)
margin = (max_e - min_e)*0.1
ax = plt.subplot(111)
ax.set_ylim(min_e - margin, max_e + margin)
ポテンシャル面と基準線、ラベルのプロット
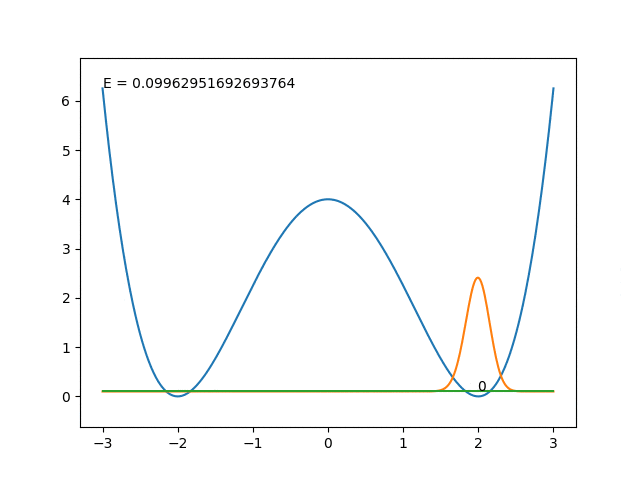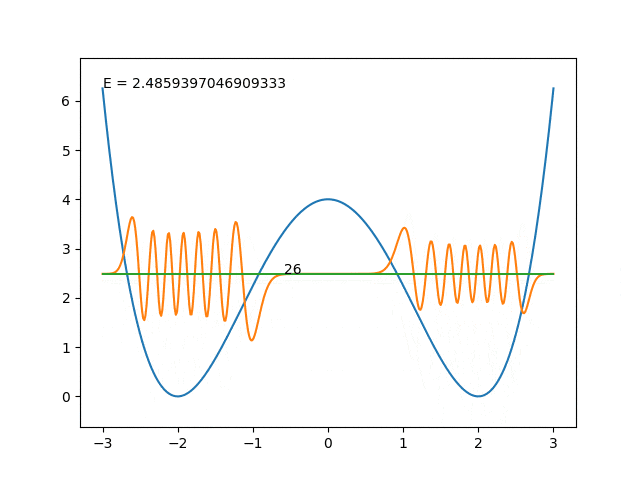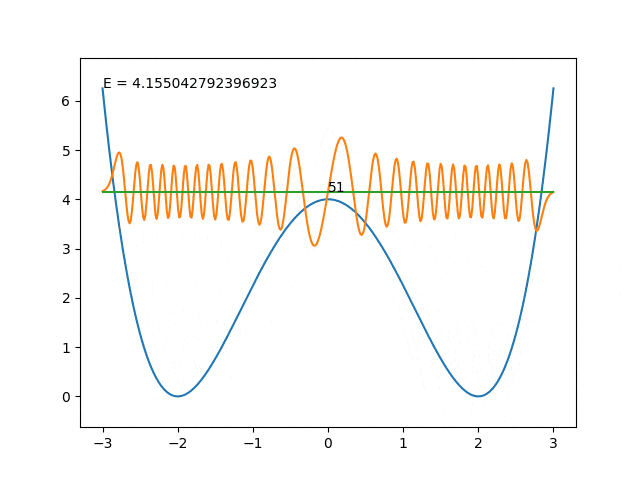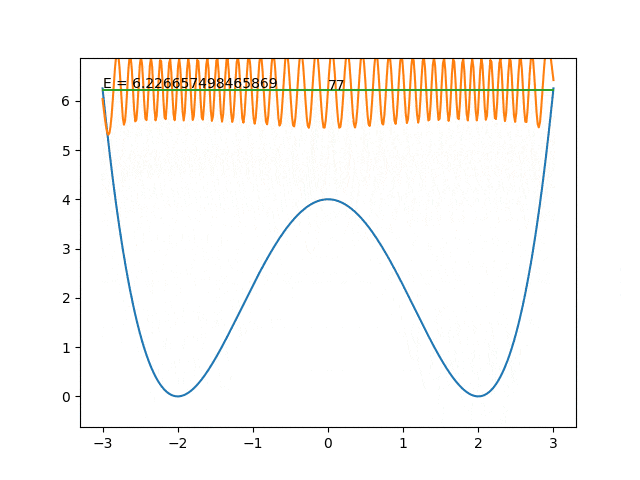
plt.plot(x, U)
line, = plt.plot(x, np.zeros(N))
label = plt.text(0, 0, "0")
en_label = plt.text(-max_x, max_U, "E = 0")
line_base, = plt.plot(x, np.zeros(N))
-
plt.plot(x, U):青色の線で、ポテンシャル面を描いています。 -
line: 下図では見えませんが、緑色の線の後ろにオレンジ色の線があります。これで波動関数(を10倍したもの)を描写します。緑色の線が$\phi_n(x) = 0$に相当するようにこれも上下移動させます。 -
line_base:緑色の線:各波動関数のエネルギーのところに表示させます。波動関数の$y=0$の線も兼ねます。 -
label: 緑色の線にある数字で、$i$番目の励起状態だと言うことを示します。横方向には $x_i = \left<\psi_i|x|\psi_i\right>$ に来るようにします。 -
en_label:左上のE = hogehogeという文字で、エネルギー順位の具体的な数字を表示します。
ここまででこのような図ができるはずです。ただplt.show()を呼び出していないので、これが目に映ることは無いでしょう。
なお、0番目の励起状態は基底状態とします。
基底状態から順に描写
for i in range(N):
# i 番目の励起状態のエネルギー
ei = W[i]
# あまり高いエネルギーに来たら止める
if max_U < ei:
break
# i 番目の励起状態の波動関数ベクトル
phi = V[:, i]
# 位置の期待値 <Ψ|x|Ψ>
xi = np.sum(phi*x*phi)
# 波動関数の描写
line.set_data(x, phi*10 + ei)
# 緑色の線を移動
line_base.set_data(x, np.zeros(N) + ei)
# ラベル更新
label.set_text("{}".format(i))
# ラベルの位置を更新
label.set_position((xi, ei))
# エネルギー表示の更新
en_label.set_text("E = {}".format(ei))
# 表示して一秒待つ
plt.pause(1.0)
plt.show() # 最後の状態でストップ
これまでのコードスニペットを1つのpythonスクリプトファイルにまとめて実行するだけで結果を確認できるはずです。
結果
十分深いときには片方の井戸に偏在していますが、エネルギー順位が高くなってくると(14番目~)エネルギー障壁を超えていないのに突然両方の井戸に波動関数が現れるようになりました。
障壁がもし無限大の高さであれば井戸の中の人からすると世界にひとつだけの井戸の中にいるのと変わらないわけで、深い時には片方だけにいることにはあまり疑問はないでしょう。
逆にエネルギー順位に対して障壁があまり高くない場合、障壁の無向の情報が洩れてきていると解釈できるかもしれません。
なお、m = 10程度だと基底状態の段階で両方の井戸に波動関数が散らばっていました。
その他
実装の妥当性
m = 1.0
U = 0.5*x**2
としてやれば
$$E_n = \hbar\omega\left(n + \frac{1}{2}\right) = n + \frac{1}{2}$$
となることを確認しています。
今後
ちょっと試してみたいことがありまして、今回の話はその準備です。