環境
- Windows 7
- Anaconda 4.3.34
- python 3.6.4
何の話か
直線群の包絡線の曲線をSympyを使って求め、matplotlibを使って可視化してみたPythonコードを、自分語りに交えて紹介します。
導入
多湖 輝氏のシリーズに「頭の体操」というものがあります。なるほど面白い問題からなぞなぞ、ただの屁理屈まで幅広いひねった問題があったように思います。
例:問「先に家を出て東に向かった兄を追って弟が家を出たが、弟は西に向かった、何故か」答「自転車がある駐車場が西にあるから」
僕が子供のころ父が買っていて読んでいたのですが、そんななかふと気になる問題がありました。
ちょっと具体的な文は忘れたのですが、要約すると
「定規だけ(つまり直線だけ)で円を描け」
というものでした。答えは
- 正方形を用意し、各辺を細かく等分したメモリを打つ
- 左下にP、右下にQを置く
- PとQを結ぶ線を引く
- Pを右に1メモリ分、Qを上に1メモリ分動かしてまたPQを結ぶ線を引く
- Pが右下に、Qが右上に達するまで続ける
- 円の右下90°の円弧が浮かび上がる
というものです。
以下のコードで実験できます。
import matplotlib.pyplot as plt
import numpy as np
graph_size = 10
plt.rcParams['figure.figsize'] = (graph_size, graph_size)
plt.axis('off')
for a in np.linspace(0, 1, 20):
plt.plot([a, 1], [0.0, a], )
plt.rcParamsは図を正方形にするためのものです。
これを実行すると以下の図になります。

当時小学校低学年程度だった僕はいたく感激し、親が持っていた当時のワープロ(液晶が白黒でうしろにプリンタが付いているタイプ)の作図機能を使って実験してみました。するとカラフルではないものの上の図のような絵が描けました。
こいつはすごいと、実際の円も重ねて描いてみました。Pythonで再現すると、以下のように$(0, 1)$を中心とした半径1の円について、$0 \le x \le 1$の範囲で$y$が小さい方をプロットすることになります。黒い点線で円弧が描かれます。
def circle(x):
return 1.0 - np.sqrt(1.0 - x**2)
x = np.linspace(0., 1.0, 100)
plt.plot(x, circle(x), color='black', linestyle='dashed', linewidth=2.)

円とちゃうやん。
解析解
示された曲線が円ではないということに気付いたものの、まだその時はそれ以上の考察する術を知らなかったため、そのうち忘れ去っていました。
高校に進んでから、微分や変分法といった方法を見かけたとき、ふとこの円もどきの問題を思い出しました。今ならこの疑問に答えられるかもしれないと解いてみました。
PythonのSympyで対応させながら考えていきます。
変数の定義
まず必要なモジュールのimport。
import numpy as np
import sympy
横軸 $x$ と、$(a, 0)$と$(1, a)$を通る直線 $g(x; a) = \frac{a}{1 - a}(x - a)$ ($ 0 \le a \le 1$) をg_axとして定義します。
x = sympy.Symbol("x")
a = sympy.Symbol("a")
g_ax = a*(x - a)/(1 - a)
この $g(x; a) = 0$ に対する包絡線が $f(x)$ です。
方針(数学の話)
包絡線の一般の解法としては $g(x; a) = 0$ の包絡線は $g(x; a) = 0$ と $\frac{\partial g(x; a)}{\partial a} = 0$ の連立方程式を解くことになります。
今回のケースについて考えてみます。
ある $x$ について注目したとき、 $a$ を様々に動かしたとき一番上に来た $g(x; a) = 0$ が $x$ における $f(x)$ の値になります。
つまりこの$x$において$g(x; a)$が最大値をとる$a$を$a_0(x)$とすると、$f(x) = g(x; a_0(x))$ となります。

この図で言うと青い線が $x$ において一番上に来る直線で、$a_0$以外の$a$ではこれより低いところしか通らないように見えます。
これは $g(x; a)$ を $a$ で微分して0になるところが極値となり、最大値であることを確かめることで求められそうです。今回は $a$ を様々に動かしたときを想像してみて、 $ 0\le x, a \le 1 $においては極値はただ一つで最大値であるとしてしまいます。
これらをまとめると、
- $\frac{\partial g(x; a)}{\partial a}(a_0) = 0$ を解いて$a_0$を$x$で書く
- その$a_0(x)$を$g(x; a)$に代入して$f(x)$を得る
という流れで、結局一般の解法に帰着しました。
Pythonで計算
まず $g(x; a)$を$a$で微分してみます。
dgda = sympy.diff(g_ax, a)
print(dgda)
-a/(-a + 1) + a*(-a + x)/(-a + 1)**2 + (-a + x)/(-a + 1)
\frac{-a}{-a + 1} + a\frac{-a + x}{(-a + 1)^2} + \frac{-a + x}{-a + 1}
これを解きます。
a_0s = sympy.solve(dgda, a)
print(a_0s)
[-sqrt(-x + 1) + 1, sqrt(-x + 1) + 1]
a_0 = \pm \sqrt{1 - x} + 1
今回は $0 \le a_0 \le 1$の方に用があります。つまり a_0s[0] で取得します。ついでに $f(x) = g(x; a_0)$ と代入して計算してしまいます。
a_0 = a_0s[0]
f = g_ax.subs(a, a_0)
print(f)
(-sqrt(-x + 1) + 1)*(x + sqrt(-x + 1) - 1)/sqrt(-x + 1)
f(x) = \frac{(\sqrt{1 - x} + 1)(x + \sqrt{1 - x} - 1)}{\sqrt{1 - x}}
なんか項が多いですね。ちょっとSymPyで整理できないか試します。Sympyには式を展開するexpandや因数分解するfactorといった関数が用意されています。
print(f.expand())
print(sympy.factor(f.expand()))
print(sympy.factor(f))
-x + 2*x/sqrt(-x + 1) + 2 - 2/sqrt(-x + 1)
-(x*sqrt(-x + 1) - 2*x - 2*sqrt(-x + 1) + 2)/sqrt(-x + 1)
-(sqrt(-x + 1) - 1)*(x + sqrt(-x + 1) - 1)/sqrt(-x + 1)
いずれもいまいち簡単になっていないですね。
プロット
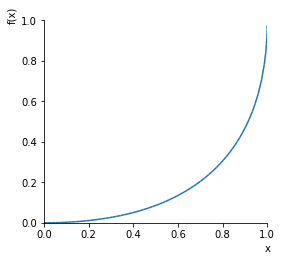
一応プロットしてみましょう。sympyはmatplotlibを使って変数とか式をプロットするモジュール plotting を持っています。普通にmatplotlibを使うときのように前もってオプションを変更することも可能です。
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (4,4)
sympy.plotting.plot(f, (x, 0, 1))
それっぽいです。後ほど正しいかどうか確認します。
結果
なお、人力で頑張った結果、
f(x) = 2 - x - 2\sqrt{1 - x}
と整理できました。
確認
最初の直線と円を引くところから繰り返し、最後にf(x)のプロットを行います。
import matplotlib.pyplot as plt
import numpy as np
def f(x):
return (2.0 - x) - 2.0*np.sqrt(1.0 - x)
def circle(x):
return 1.0 - np.sqrt(1.0 - x**2)
graph_size = 10
plt.rcParams['figure.figsize'] = (graph_size, graph_size)
plt.axis('off')
for a in np.linspace(0, 1, 20):
plt.plot([a, 1], [0.0, a], )
x = np.linspace(0., 1.0, 100)
plt.plot(x, circle(x), color='black', linestyle='dashed', linewidth=2.)
plt.plot(x, f(x), color='black')
実行するとこんな感じです。

一応正しいようですが、最初の図と重ねて点滅させてみます。

結論
具体的に式も分かり、どう見ても円ではないよなあ、と確認できました。
高校の時はPythonというかコンピュータで記号演算するという発想がなかったので、これを手で計算していましたが、結局は$\sqrt{1 - x}$のような項が現れたように記憶しています。
円と同じ曲がり方になるには $\sqrt{1 - x^2}$ とかでないといけないでしょう。
まあ、頭の体操にはこういう感じの適当な問題もあったということです。
その他
ちなみに、曲線の正体は放物線でした。右下の角を中心に時計回りに45°回転させてみてください。
頑張れば代数的に計算できて、放物線の式 $ax^2 + bx + c$に帰着できるかと思います。
ていうか最初から $g(x; a)$ を45°傾けて定義すればよかったのでは。