前の記事
https://qiita.com/sage-git/items/5c668a78d75a1b0aaaf1
で、周囲のマスの1を数えるのにconvolution2dとかでできそうだと言いましたが、
やってみたところ思いの外簡単に出来たのでメモしておきます。
Python
% python --version
Python 3.5.2
この他、numpy、scipy、OpenCVをインストールしています。
下ごしらえ
系の初期設定
N = width*height
v = np.array(np.random.rand(N) + init_alive_prob, dtype=int)
F = v.reshape(height, width)
NumpyでN個の$(0, 1)$の乱数の配列を作り、init_alive_probだけ底上げし、
np.array()にそれを渡してdtype=intで型変換して切り捨てて、
height、widthの形の2次元配列にしてFに代入します。
周囲の個数カウント
0または1を要素にもつint型のNumpy配列Fについて、自身を含む周囲9マスの1の個数は
mask = np.ones((3, 3), dtype=int)
signal.correlate2d(F, mask, mode="same", boundary="wrap")
となります。
F
0 1 1 0 0 0
1 0 1 0 0 1
0 1 0 0 0 0
0 0 1 1 0 0
1 1 0 0 0 1
1 1 1 1 0 1
signal.correlate2d(F, mask, mode="same", boundary="wrap")
6 7 6 4 3 4
4 5 4 2 1 2
3 4 4 3 2 2
4 4 4 2 2 2
6 6 6 4 4 4
7 7 6 3 3 4
配列の出力
なお、先ほどの行列部分の出力は
np.savetxt(sys.stdout, F, fmt="%d")
でできます。
次の世代
ある世代での状態FについてNをsignal.correlate2dで数えた周囲9マスの生存セルの数を持つ行列とすると、次の世代では
-
Nが3の要素は必ず1 -
Nが4の要素はF値をそのまま継続 - それ以外の要素では必ず0
となります。これを整理しますと、$(N = 3) \vee ( F \land (N = 4) )$ とできます。
(あるいは、$S$を生存するときの周囲の数の集合、$B$を誕生するときの周囲の数の集合とすると、次の世代で生存セルであるかどうかというのは
\left(\bigvee_{k\in S}(N = k + 1)\wedge F\right)\vee\left(\bigvee_{k\in B}(N = k)\wedge (\lnot F)\right)
と一般化できて、今回のようなB3/S23だと$S=\{2, 3\}$、$B=\{3\}$ですので、これを代入して展開すると$(N = 3) \vee ( F \land (N = 4) )$になります。)
これをnumpyの言葉にしますと、
G = np.array(N == 3, dtype=int) + F * np.array(N == 4, dtype=int)
もしくは暗黙の型変換に頼って
G = (N == 3) + F * (N == 4)
とすればGは次の世代の行列となります。
F
1 0 0 1 1 0
0 1 1 0 0 0
1 0 0 0 1 1
1 0 0 1 1 0
1 0 0 1 1 0
0 1 0 0 0 1
G
1 0 0 1 1 1
0 1 1 0 0 0
1 0 1 0 1 0
1 1 0 0 0 0
1 1 1 1 0 0
0 1 1 0 0 0
ループ
- 配列初期設定
init_state - 次の世代を計算する
next_generation - 状態を出力する
print_state
とすると
F = init_state()
while True:
print_state(F)
F = next_generation(F)
が基本的な骨組みとなります。
画像化
どうせならOpenCVを使って画像をリアルタイムで見ようと思います。
状態Fをscale倍しつつ画像にする関数は
def to_image(F, scale=3.0):
img = np.array(F, dtype=np.uint8)*255
W = int(F.shape[1]*scale)
H = int(F.shape[0]*scale)
img = cv2.resize(img, (W, H), interpolation=cv2.INTER_NEAREST)
return img
として、グレースケールの画像ができます。
プログラム
以上の話を1つのプログラムとしてまとめます。
# !/usr/bin/python
from __future__ import print_function
import sys
import numpy as np
from scipy import signal
import cv2
mask = np.ones((3, 3), dtype=int)
def init_state(width, height, init_alive_prob=0.5):
N = width*height
v = np.array(np.random.rand(N) + init_alive_prob, dtype=int)
return v.reshape(height, width)
def count_neighbor(F):
return signal.correlate2d(F, mask, mode="same", boundary="wrap")
def next_generation(F):
N = count_neighbor(F)
G = (N == 3) + F * (N == 4)
return G
def to_image(F, scale=3.0):
img = np.array(F, dtype=np.uint8)*255
W = int(F.shape[1]*scale)
H = int(F.shape[0]*scale)
img = cv2.resize(img, (W, H), interpolation=cv2.INTER_NEAREST)
return img
def main():
p = 0.08
F = init_state(100, 100, init_alive_prob=p)
ret = 0
wait = 10
while True:
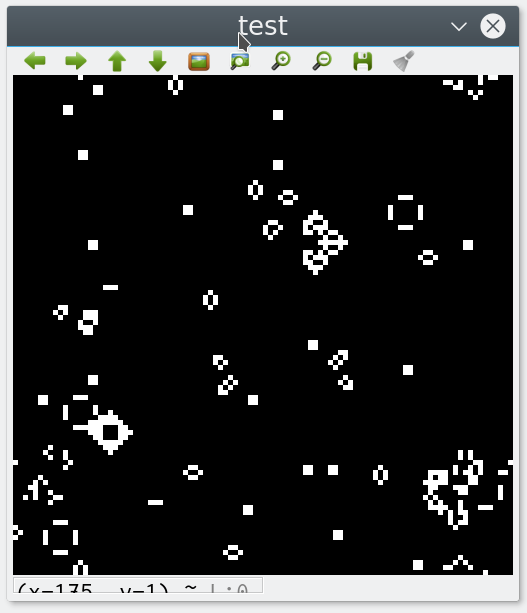
img = to_image(F, scale=5.0)
cv2.imshow("test", img)
ret = cv2.waitKey(wait)
F = next_generation(F)
if ret == ord('r'):
F = init_state(100, 100, init_alive_prob=p)
if ret == ord('s'):
wait = min(wait*2, 1000)
if ret == ord('f'):
wait = max(wait//2, 10)
if ret == ord('q') or ret == 27:
break
if ret == ord('w'):
np.savetxt("save.txt", F, "%d")
if ret == ord('l'):
if os.path.exists("save.txt"):
F = np.loadtxt("save.txt")
cv2.destroyAllWindows()
if __name__ == "__main__":
main()
盤面を100x100とし、500x500 pxの画像を生成して再生します。
また、初期の生存セルの割合を消費税程度(2018/5/19現在)としました。
これをlifegame.pyとして、python lifegame.pyと実行すると、
OpenCVの画像表示ウィンドウが立ち上がり、リアルタイムで世代が進む様子を見られます。
とりあえず定義している操作
-
r:リセット -
qまたはEsc: 終了 -
s:遅く -
f:早く -
w:現在の状態をsave.txtに保存 -
l:save.txtから読み込み現在の状態とする
sまたはfで調整できる速度には上限・下限を設けています。
save.txtのフォーマットは配列の出力の節のような、スペース区切り形式です。
フォーマットエラーの時や0``1以外の値があった時の処理は、コードを見れば分かるように特に何もしていません。
その他
Wikipediaのライフゲーム関係の記事、すごい充実している気がします。