言いたいこと
なんか最小二乗法の式いじってたら離散フーリエ変換と同じ形の式にたどり着いたのでまとめておこうと思います。
高校数学しか使ってないかと。
状況
時間に関する関数 $y(t)$ があるとします。これを離散フーリエ変換すると
y(t) = \frac{1}{\sqrt{N}}\sum_{n = 0}^{N-1} c_n\exp\left(-\mathrm{i} \frac{2\pi nt}{N}\right)
ですが、この展開係数を得るには
c_n = \frac{1}{\sqrt{N}}\sum_{t = 0}^{N-1} y(t)\exp\left(\mathrm{i} \frac{2\pi nt}{N}\right)
とします。これは行列で書いてみると
\left( \begin{matrix} c_0 \\ c_1 \\ \vdots \\ c_{N-1}\end{matrix}\right)
= \left( \begin{matrix}
W^0 & W^0 & \cdots & W^0 \\
W^0 & W^{-1} & & W^{-(N - 1)} \\
\vdots & & \ddots & \vdots\\
W^0 & W^{-(N-1)} & \cdots & W^{-(N-1)(N-1)}
\end{matrix} \right)
\left( \begin{matrix} y(0) \\ y(1) \\ \vdots \\ y(N-1)\end{matrix}\right)
と書けます。ここで $W = \exp\left(2\pi\mathrm{i}/N\right)$、でよかったっけ。
最小二乗法として解釈
時系列 $y(t_j)$ が与えられたとします。
サンプリングされた時刻 $t_j$ は等間隔で $t_j=j\Delta t$ と書けるとします。また、 $M$ 点でサンプリングされたとします。つまり、 $j = 0, 1, 2, \cdots, M- 1$ です。
一方で、周波数 $\omega_k$ の周期関数があるとします。
$$
\psi_n(t) = c_n\exp\left(\mathrm{i}\omega_n t\right)
$$
$c_n = r_n\exp(i\phi_n)$ は複素数で、動径 $r_n$ は振幅、$\phi_n$ は初期位相に相当します。
この周期関数は $N$ 個あるとします。また周波数は等間隔 $\omega_k = k\Delta\omega$ の値をとるとします。
時刻 $t_j$ の点に注目し、
y(t_j) = \sum_n c_n\psi_n(t_j)
の形で書き、複素数 $c_n$ を動かして近似、フィットしてやることを考えます。
$$
\vec{X} = \left(c_0, c_1, \cdots, c_{N-1}\right)^\mathrm{T}
$$
のベクトルが求めたい係数たちです。
添え字 $n$ についての和をベクトルの内積だと思うと、
$$
y(t_j) = \vec{\psi}(t_j)^T\vec{X}
$$
みたいな感じで書けます(後々のため、$\psi$と$X(c)$の積の順番を入れ替えています)。
ここで、$\vec{\psi}(t_j)$ は時刻 $t_j$での $\psi$ の値を並べたものです。
\vec{\psi}(t_j) = (\psi_0(t_j), \psi_1(t_j), \cdots, \psi_{N-1}(t_j))^\mathrm{T}
これををさらに添え字 $j$ について縦方向に並べると、
$$
\vec{y} = \boldsymbol{A}\vec{X}
$$
となりますが、ここで
$$
\vec{y} = \left(y(t_0), y(t_1), \cdots, y(t_M)\right)^T
$$
はベクトル、
\boldsymbol{A} =\left(\vec{\psi}(t_0), \vec{\psi}(t_1), \cdots, \vec{\psi}(t_{M-1})\right)
は$M$行$N$列の行列で書けます。特に、$N=M$ のとき正方行列になります。
わかりやすくなるかどうかわかりませんが、$\vec{y}=\boldsymbol{A}\vec{X}$を具体的に書いてみると
\left( \begin{matrix}
y(t_0) \\ y(t_1) \\ y(t_2) \\ \vdots \\ y(t_{M-1})
\end{matrix} \right)
=
\left( \begin{matrix}
\exp(\mathrm{i}t_0\omega_0) & \exp(\mathrm{i}t_0\omega_1) &
\exp(\mathrm{i}t_0\omega_2) & \cdots & \exp(\mathrm{i}t_0\omega_{N-1}) \\
\exp(\mathrm{i}t_1\omega_0) & \exp(\mathrm{i}t_1\omega_1) &\exp(\mathrm{i}t_1\omega_2) & \cdots & \exp(\mathrm{i}t_1\omega_{N-1}) \\
\exp(\mathrm{i}t_2\omega_0) & \exp(\mathrm{i}t_2\omega_1) &\exp(\mathrm{i}t_2\omega_2) & & \exp(\mathrm{i}t_2\omega_{N-1}) \\
\vdots & & & \ddots & \vdots\\
\exp(\mathrm{i}t_{M-1}\omega_0) & \exp(\mathrm{i}t_{M-1}\omega_1) &\exp(\mathrm{i}t_{M-1}\omega_2) & \cdots & \exp(\mathrm{i}t_{M-1}\omega_{N-1})
\end{matrix} \right)
\left( \begin{matrix}
c_0 \\ c_1 \\ c_2 \\ \vdots \\ c_{N-1}
\end{matrix} \right)
ここで、$N=M$ として、$e^{\mathrm{i}\Delta t\Delta\omega^2}=W$と書けば $\exp(\mathrm{i}t_j\omega_k)=\exp\left(\mathrm{i}jk\Delta\omega\Delta t\right)=W^{jk}$ ということで、
\boldsymbol{A} = \left( \begin{matrix}
1 & 1 & 1& \cdots & 1 \\
1 & W & W^2 & \cdots & W^{(N-1)} \\
1 & W^2 & W^4 & & W^{2(N-1)} \\
\vdots & & & \ddots & \vdots\\
1 & W^{(N - 1)} & W^{2(N-1)} & \cdots & W^{(N-1)^2}
\end{matrix} \right)
となります。いま求めたい$\vec{X}$は $\vec{y} = \boldsymbol{A}\vec{X}$ の両辺から $\boldsymbol{A}$ の逆行列を掛けた
$$
\vec{X} = \boldsymbol{A}^{-1}\vec{y}
$$
ですが、$\boldsymbol{A}^{-1}$ は高速フーリエ変換で出てくる行列の形に似たものとなります。
\boldsymbol{A}^{-1} = \frac{1}{N}\left( \begin{matrix}
1 & 1 & 1& \cdots & 1 \\
1 & W^{-1} & W^{-2} & \cdots & W^{-(N-1)} \\
1 & W^{-2} & W^{-4} & & W^{-2(N-1)} \\
\vdots & & & \ddots & \vdots\\
1 & W^{-(N - 1)} & W^{-2(N-1)} & \cdots & W^{-(N-1)^2}
\end{matrix} \right)
疲れたのでさぼりますが、もっと頑張ればDFTと同じ式になるんじゃないかなと。
対応だけ取るとDFTでは $W = \exp\left(2\pi\mathrm{i}/N\right)$ に対して最小二乗法では $W =\exp\left(\mathrm{i}\Delta\omega\Delta t\right)$ です。
追記
誤差(またはそれが正規分布すると仮定したときの対数尤度)
L(\vec{x}) = \left(\vec{y} - \boldsymbol{A}\vec{x}\right)^\mathrm{T}\cdot\left(\vec{y} - \boldsymbol{A}\vec{x}\right)
が最小にするとした最小二乗法をきちんと求めた式は
\vec{x} = (\boldsymbol{A}^\mathrm{T}\boldsymbol{A})^{-1}\boldsymbol{A}^\mathrm{T}\vec{y}
ですが、$M=N$、$\Delta\omega\Delta t = 2\pi/N$ という条件下では $\boldsymbol{A}^\mathrm{T} = \boldsymbol{A}$で、さらに周期関数 $\{\psi_n(t)\}$ が直交基底系なら $\boldsymbol{A}^\mathrm{T}\boldsymbol{A}=N\boldsymbol{I}$ で、$\boldsymbol{A}^{-1} = \frac{1}{N}\boldsymbol{A}$ が言えると思いますので、
$$
\vec{X} = \boldsymbol{A}^{-1}\vec{y}
$$
に落ち着くのではと思います。
おまけ
軽くpythonで確かめてみます。
f は長さ nlen の実数配列(1次元のnumpy配列)とします。
まずは普通のフーリエ変換、ですが結果を実数にするというだけのために離散コサイン変換を使います。
from scipy import fftpack
def DCT(f):
return fftpack.dct(f)
次にcosの合計でフィットする方法で求めてみます。
import numpy as np
def lsq(f):
nlen = len(f)
dw = np.pi/nlen
w = np.arange(nlen)*dw
t = np.arange(nlen)
phi = np.tile(w, (nlen, 1))*(t.reshape(nlen, 1))
X = np.cos(phi)
g = np.linalg.solve(X, f)
return g*nlen
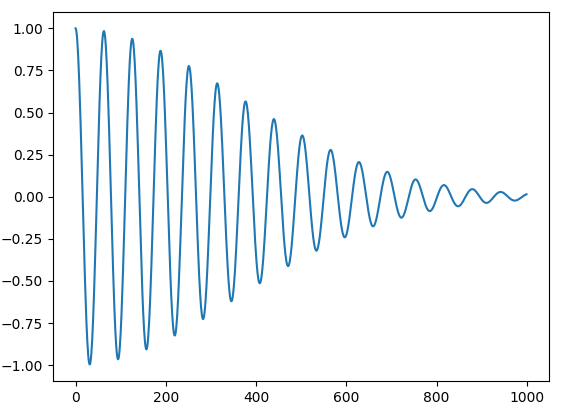
データを作ります。普通の振動に軽くガウシアンを掛けます。
nlen = 1000
x = np.arange(nlen)
f = np.cos(x/10)*np.exp( - (x)**2/(nlen/2)**2)
import matplotlib.pyplot as plt
plt.plot(x, f)
plt.show()
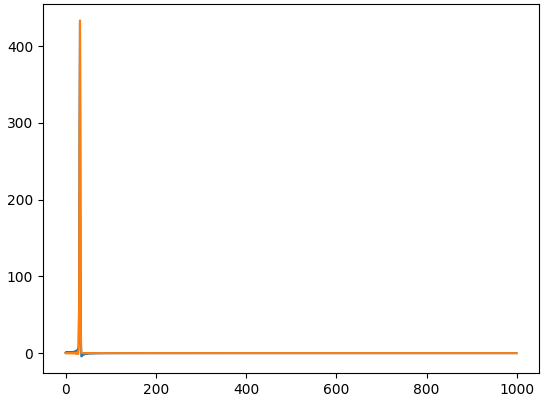
2通りの方法でフーリエ変換しつつ、プロットします。
g_lsq = lsq(f)
g_dct = DCT(f)
plt.plot(x, g_dct)
plt.plot(x, g_lsq)
plt.show()
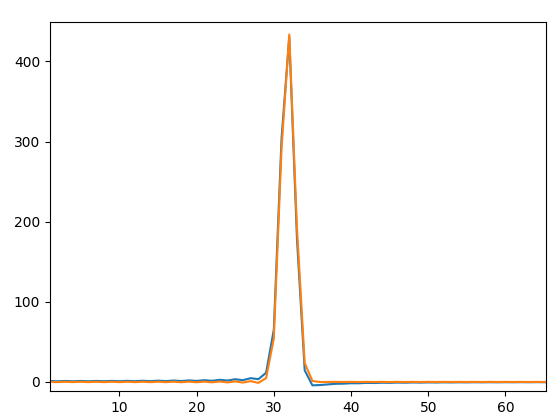
ピークを拡大。
細部がずれてしまうのですが、ピーク位置と高さ、幅が合ってるのでよしとします。
まとめ
なんか適当な関数を三角関数の和で書くとき、三角関数を基底関数系と思ってその性質を使えば離散フーリエ変換に、関数フィッティングだと思えば最小二乗法になるのですが、最小二乗法のほうの条件を整えてやるとフーリエ変換と同じ形になった、という気づきです。