半量子動力学シミュレーション：古典的ガウス波束

計算が重たい量子ダイナミクスを古典力学的の発展で何とかしようとする話というのは何種類かあります。今回はそのうちの１つ、ガウス波束を古典力学に組み込む方法をやってみます。

（編集：タイトルとタグですが、投稿直後は半古典としていましたが、半量子動力学としました。）

準備

静止した1次元のガウス波束

中心位置 $r$ で静止した、幅 $G$ の波束を考えます。空間は $x$ の1次元とします。

$$
\phi(r) = N\exp\left(-\frac{(x-r)^2}{4G^2}\right)
$$

規格化因子 $N = (2\pi G^2)^{-1/4}$ は $\int_{-\infty}^\infty \phi^\dagger\phi dx = 1 $ から決まります。

一次元の平面波

一方で、自由粒子の1次元時間発展シュレーディンガー方程式

$$
i\hbar\frac{\partial \phi}{\partial t} = -\frac{1}{2}\frac{\partial^2 \phi }{\partial x^2}
$$

の解は波数の固有関数でもある平面波です。

$$
\psi_k (x, t) = \frac{1}{2\pi}\exp\left(ikx - i\omega_k t\right)
$$

進行するガウス波束

この平面波を重ね合わせてガウス波束を作ることをします。まず $t=0$ のときを最初のガウス波束の表式になるようにして、 $r = vt$ と等速運動を考えます。いろいろやって一般の時刻 $t$ についての表式を得ると

$$
\psi(x, t) = \frac{1}{\sqrt{2\pi(G(t))^2}}\exp\left(ik_0 x - i\omega_0 t - \frac{(x - vt)^2}{4(G(t))^2}\right)
$$

となります。ここで幅 $G(t)$ は時間の関数となり、

$$
G(t)^2 = G_0^2 + \left(\frac{\hbar t}{2mG_0^2}\right)^2
$$

と自由粒子の波束がひろがる様子が分かります。

参考

半古典モデル

導入

運動するガウス波束に対し以下のような仮定を考えます。

• 波束の中心位置と幅が時間変化
• ガウス波束としての形は崩れない
• 波束の幅が時間発展するので、これに共役な運動量を考える

3番目の仮定がポイントで、これで波束の幅の変化量を運動量とし、ハミルトニアンを定義してやり、適当な時間発展法で解いてやります。

すると、量子的な波束の性質を保ったまま、古典力学の計算量でシミュレーションをできるんじゃないかと期待できます。

波束

1次元系の1粒子では、波束の中心座標とその運動量 $(r, p)$、波束の幅とその共役運動量 $(G, K)$ を与えると波束を特徴付けられるとします。すると $r, p, G, K $ の4つの変数が位相空間を張るとみなせます。この時の波束は

$$
\psi(x, t; r, p, G, K) = N\exp\left(A(t)(x - r)^2 + ip(x - r)\right)
$$

$$
A(t) = - \frac{1}{4G^2} + \frac{iK}{\hbar G}\\
N(t) = (2\pi G(t)^2)^{-1/4}
$$

と書けます。ここで $i$ は虚数単位です。

ハミルトニアン

質量を $m$、ポテンシャルを $V(x)$ として、拡張ハミルトニアンを書いてみます。ここで問題になるのが運動量エネルギーです。波束中心位置については、古典的には粒子の座標になるため、対応する質量は粒子の質量です。一方、波束の幅に対する質量は自明ではないです。ただ波束の幅の質量は粒子としての質量に比例しそうですし、潔く粒子の質量と同じにしてしまいます。チェックはしてません。
そうするとハミルトニアンは運動エネルギーと拡張したポテンシャルの和で

$$
H_\mathrm{ext}(r, p, G, K) = \frac{p^2 + K^2}{2m} + V_\mathrm{ext}(r, p, G, K)
$$

$$
V_\mathrm{ext}(r, p, G, K) = \frac{\hbar^2}{8mG^2} + \left< V\right>
$$

です。添え字の $\mathrm{ext}$ は拡張した量であることを表します。
うまく次元を調整して $m$ と $\hbar$ を $1$ とすると表記がすっきりしそうです。

ポテンシャル

ポテンシャルの平均値 $ \left< V\right>$ はガウス関数を掛けて積分するものになるため、解析的に積分できる量は限られてきます。
ここでは、W型のdouble wellポテンシャルになる４次多項式を使い、トンネル効果を見てみようと思います。

$$
V(x) = -\frac{a}{2}x^2 + \frac b 4 x^4
$$

まずはポテンシャルの期待値を計算しておきます。 $\left< V\right> = \left< \psi|V|\psi\right>$ は共役の積なので、expの虚部は無くなります。後は多項式が掛かったガウス積分です。

$$
\left< V\right>(x, G) = \int_{-\infty}^\infty dxA^2\left(-\frac{a}{2}x^2 + \frac b 4 x^4\right)\exp\left(- \frac{1}{2G^2}(x - r)^2\right) \\
= V(r) -\frac{1}{2}aG^2 + \frac{3}{2}br^2G^2 + \frac{3}{4}bG^4
$$

時間発展

ハミルトニアンが書けたので、時間発展演算子を準備します。一般論として、位相空間の点 $z(t) = (q(t), p(t))$、ポンテンシャル $V(q)$ 、運動量 $T(p) = p^2/2m$ とします。
ハミルトン運動方程式はポアソン括弧とその演算子表記で

$$
\dot{z} = \left\{ z, H \right\} \equiv D_Hz
$$

と書け、形式解は $z(t + \tau) = \exp\left(\tau D_H\right)z(t)$ となります。
運動エネルギーと位置エネルギーはただの足し算ですので、 $ \exp\left(\tau D_H\right) = \exp\left(\tau (D_T + D_V)\right)$ です。

ここで、 $\exp\left(\tau D_T\right)$ と $\exp\left(\tau D_V\right)$ は具体的に書き下せます。

まず単独の演算子を確認しますと、

$$
D_Tz = \left\{ z, T \right\} = \frac{\partial z}{\partial q} \frac{\partial T}{\partial p} - \frac{\partial z}{\partial p} \frac{\partial T}{\partial q} = (1, 0)\frac{p}{m} - 0 = (\frac{p}{m}, 0)
$$

$$
D_Vz = \left\{ z, V \right\} = \frac{\partial z}{\partial q} \frac{\partial V}{\partial p} - \frac{\partial z}{\partial p} \frac{\partial V}{\partial q} = 0 - (0, 1)\frac{\partial V}{\partial q} = \left(0, - \frac{\partial V}{\partial q}\right)
$$

です。また、

$$
\dot{z} = \left(\dot{q}, \dot{p}\right)
$$

$$
\dot{z} = D_H z = \left(D_T + D_V\right) z = \left(\frac{p}{m}, - \frac{\partial V}{\partial q}\right)
$$

という関係もあるので、それぞれ時間微分を計算する演算子であり、 $q$ に対する速度、$p$ に対する力に対応します。さらにもう一度作用させた $D_TD_Tz$ や $D_VD_Vz$ は $0$ になります。これを踏まえると

$$
\exp\left(\tau D_T\right)z(t) = z(t) + \tau D_Tz(t) + \frac{1}{2}\tau^2 D_TD_Tz(t) + \cdots = z(t) +\tau\frac{p(t)}{m}
$$

$$
\exp\left(\tau D_V\right)z(t) = z(t) + \tau D_Vz(t) + \frac{1}{2}\tau^2 D_VD_Vz(t) + \cdots = z(t) - \frac{\partial V(q)}{\partial q}(t)
$$

と、よく見る位置と運動量の更新式となります。
あとは形式的な $\exp\left(\tau D_H\right) = \exp\left(\tau (D_T + D_V)\right)$ を $\exp\left(\tau D_T\right)$ と $\exp\left(\tau D_V\right)$ で展開します。この仕方は参考論文など何か参考書を見るかググってください。

また、 $q$ と $p$ がそれぞれ多次元であっても、面倒なのは $V(q)$ の中身くらいで、時間発展演算子については各成分ごとに処理すればいいでしょうから、特に難しい応用でもないです。

今回は2次の精度で展開した

$$
\exp\left(\tau D_H\right) = \exp\left(\frac \tau 2 D_T\right)\exp\left(\tau D_V\right)\exp\left(\frac \tau 2 D_T\right)
$$

を使います。なお、 $D_T$ と $D_V$ を入れ替えたものも同精度ですが、一番計算コストが高いのは $V(q)$ の微分で、これは $\exp\left(\tau D_V\right)$ に含まれますので、 $\exp\left(\tau D_V\right)$ ができるだけ少ない展開を選びます。

参考論文

高次シンプレクティック数値積分法の設計
https://www.sciencedirect.com/science/article/abs/pii/0375960190900923?via%3Dihub

位置の時間微分

よく見る速度（運動量を質量で割ったもの）が得られます。

$$
\dot{r} = \frac{\partial H}{\partial p} = \frac{p}{m}
$$

$$
\dot{G} = \frac{\partial H}{\partial K} = \frac{K}{m}
$$

運動量の微分

古典であればポテンシャルの位置微分ですが、今回は余計なものがついてきます。

$$
\dot{p} = - \frac{\partial H}{\partial p} = ar - br^3 - 3brG^2
$$

$$
\dot{K} = - \frac{\partial H}{\partial K} = aG -3br^2G - 3bG^3 + \frac{\hbar}{4mG^3}
$$

ちなみに $\dot{K}$ の最後の項ですが、自由粒子でも出てくる項で必ず正なので、波束が広がる様子を表現していると言えます。

あとは可換・非可換に気を付けて時間発展のソルバを組み立てていきます。
例えば $\dot{r}$ と $\dot{G}$ の部分に対応する積分は可換っぽいですが、それ以外は非可換に見えます。

Juliaで

これで各座標の時間微分が分かりましたので、時間発展演算子を書くことができます。それをコードに落としていきます。

まずは波束を決める量を構造体にまとめ、波動関数を定義します。それと物理量を定数にしておきます。

struct wavepacket
    r # center
    G # width of the wavepacket
    p # conjugate momentum of x
    K # conjugate of G
end

ħ = 1.0
m = 4.0

function ϕ(x, wp:: wavepacket)
    A = (-1 + 2*im*ħ*wp.G*wp.K)/(4.0*wp.G^2)
    N = (2*pi*wp.G^2)^(-1.0/4.0)
    e = A*(x - wp.r)^2 + im*wp.p*(x - wp.r)
    return N*exp(e)
end

質量が $1$ ではないですが、この後決めるポテンシャルのパラメータでは質量を $1$ にすると軽すぎて2重井戸として成立しないので、極小が原点ではなくなる最低限の重さにしました。
系のポテンシャル、ハミルトニアンを定義します。ポテンシャルにパラメータ$a, b$ がありますが、これもグローバル定数にしてしまいます。

a = 4.0
b = 4.0
function V(x)
     - a*x^2/2 + b*x^4/4
end

function Vext(wp::wavepacket)
    ϕVϕ = -0.5*(a - 3*b*wp.r^2)*wp.G^2 + 0.75*b*wp.G^4 + ħ^2/(8*m*wp.G^2)
    return V(wp.r) + ϕVϕ
end

function kinetic_en(wp::wavepacket)
    (wp.p^2 + wp.K^2)/(2*m)
end

function Hamiltonian(wp::wavepacket)
    return Vext(wp) + kinetic_en(wp)
end

各物理量の時間微分です。

function rdot(wp::wavepacket)
    return wp.p/m
end

function Gdot(wp::wavepacket)
    return wp.K/m
end

function pdot(wp::wavepacket)
    return a*wp.r - b*wp.r^3 - 3*b*wp.r*wp.G^2
end

function Kdot(wp::wavepacket)
    return (a - 3*b*wp.r^2)*wp.G - 3*b*wp.G^3 + ħ^2/(4*m*wp.G^3)
end

時間積分のパーツを用意します。

function timestep_X(wp::wavepacket, dt)
    newr = wp.r + dt*rdot(wp)
    newG = wp.G + dt*Gdot(wp)
    return wavepacket(newr, newG, wp.p, wp.K)
end

function timestep_P(wp::wavepacket, dt)
    newp = wp.p + dt*pdot(wp)
    newK = wp.K + dt*Kdot(wp)
    return wavepacket(wp.r, wp.G, newp, newK)
end

そしてSymplectic差分法での積分ルーチン。

function timestep(wp::wavepacket, dt)
    wp1 = timestep_X(wp, dt*0.5)
    wp2 = timestep_P(wp1, dt)
    wp3 = timestep_X(wp2, dt*0.5)
    return wp3
end

最後に計算本体のルーチン。
以下の例では初期位置の波束を中心 $r = 0.82$　、幅 $G=0.32$ として、速度は$r$ について正の方向に少しあたえました。これや dt は状況に応じていろいろ変えていきます。

wp_init = wavepacket(0.82, 0.32, 0.5, 0.0)
wp_prev = wp_init
dt = 0.001
for i in 1:10000
    wp = timestep(wp_prev, dt)
    wp_prev = wp
end

初期位置の決め方

この初期位置ですが、適当な位置から運動量に減衰を与えてMDを行うと極小値に落ち着きそうという発想で作っています。

function timestep_P(wp::wavepacket, dt)
    newp = wp.p + dt*pdot(wp)
    newK = wp.K + dt*Kdot(wp)
    newp = newp*0.999
    newK = newK*0.999
    return wavepacket(wp.r, wp.G, newp, newK)
end
wp_init = wavepacket(0.5, 0.5, 0.0, 0.0)

このケースでは減衰係数は $0.999$ ですが、 $dt$ などのパラメータにより決めたらよいと思います。
また、原点付近で波束を広げて両側の井戸の底を感じることで $V_\mathrm{ext}$ を小さくするため、原点は極小値となります。なのである程度原点からずらしたところから始めないと原点に収束します。

可視化

ただこれだけではメモリの数値が変わるだけの何も表示されないプログラムです。時間発展の様子を図で表示してみます。

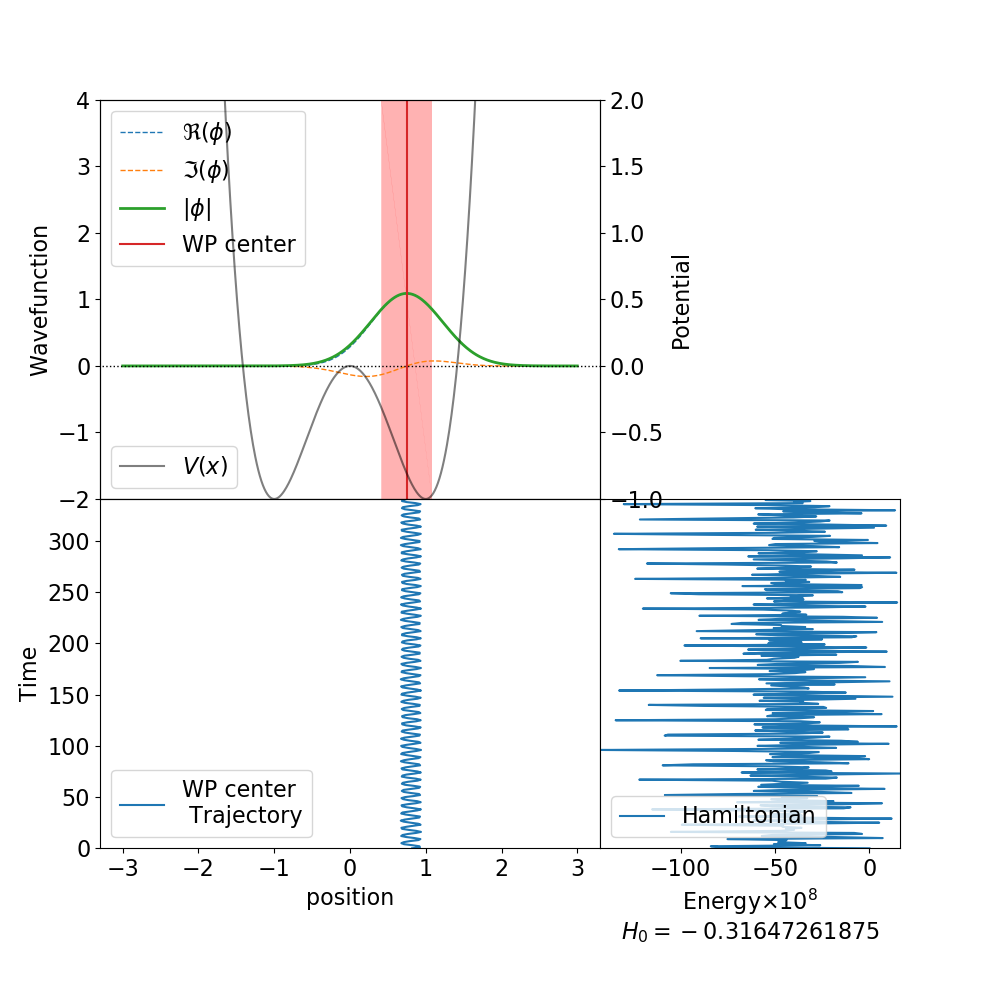
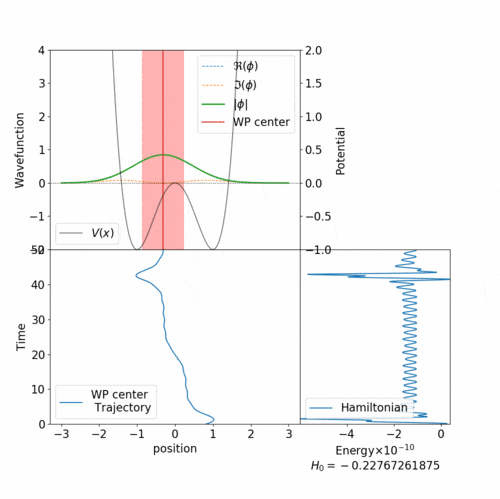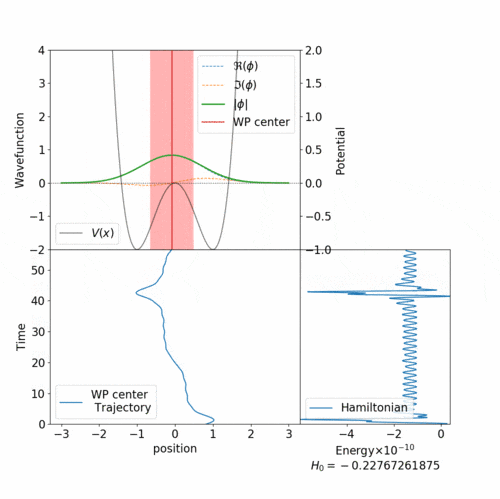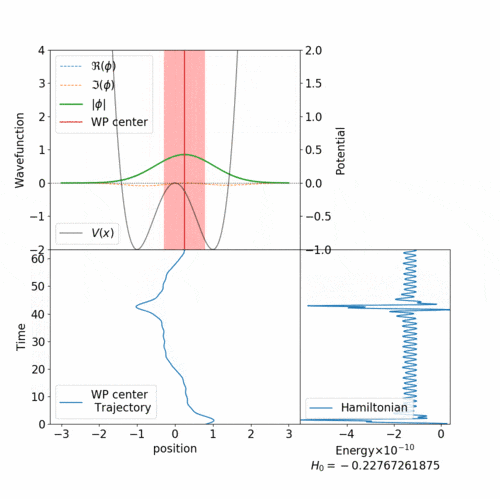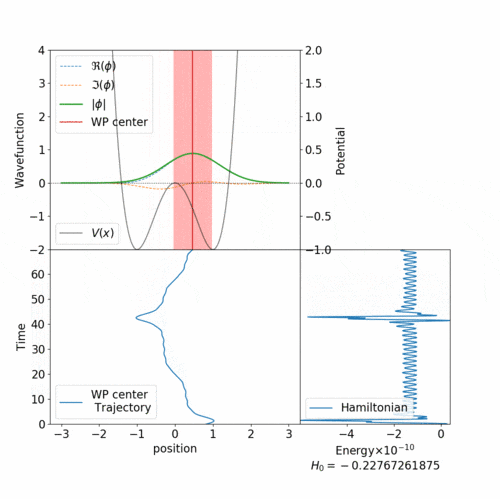
上図のようなアニメーションを作ってみます。（なおこの図は上のプログラム中のパラメータではなく試行錯誤中の様子の１つですので、この記事中のプログラムを集めて実行してもこの図の通りにはなりません）
PyPlotの解説記事のつもりではないので、各行の詳しい説明は省きます。

まず必要なパッケージを読み込みます。 PyCall は無くてもいいかもしれない。

using PyPlot
using PyCall
pygui(true)

初期値での状態を計算します。また、軌跡記録用に配列を準備します。xs や ϕs、 Vs は波動関数やポテンシャルの概形をプロットするための配列です。 s を付けて複数形にすることで配列だと示しています。xmin と xmax は波束の幅の左端、右端のx座標です。この間を塗りつぶし、波動関数の広がりを可視化したいと思います。

xs = [i*0.01 - 3.0 for i in 0:600]
ϕs = [ϕ(x, wp_init) for x in xs]
Vs = V.(xs)

H0 = Hamiltonian(wp_init)

traj_T = [0.0]
traj_H = [0.0]
traj_r = [wp_init.r]

xmin = wp_init.r - wp_init.G
xmax = wp_init.r + wp_init.G

グラフは波動関数、中心位置の軌跡、エネルギーの記録の3つがありますので、それらのsubplotを作ります。

ymin = -2
ymax = 4
fig = PyPlot.figure(figsize=(10, 10))
PyPlot.rc("font", size=16)
ax_ϕ = fig.add_axes((0.1, 0.5, 0.5, 0.4), ylim=[ymin, ymax] )
ax_traj = fig.add_axes((0.1, 0.15, 0.5, 0.35), sharex=ax_ϕ)
ax_en = fig.add_axes((0.6, 0.15, 0.3, 0.35), sharey=ax_traj)
ax_en.axes.yaxis.set_visible(false)
ax_V = ax_ϕ.twinx()

ax_ϕ.set_ylabel("Wavefunction")
ax_traj.set_ylabel("Time")
ax_traj.set_xlabel("position")
ax_V.set_ylabel("Potential")
ax_en.set_xlabel("Energy\n\$H_0 = $H0\$")
ax_V.set_ylim([-1, 2])

add_subplot では今回のやりたいことの設定は難しそうだったので、より一般的な add_axis を使うことにします。
ax_ϕ は波動関数用、ax_V はポテンシャル用でこれらは一番上のグラフに描写します。
ax_traj は左下のパネルで中心座標の軌跡をプロットし、横軸 x を波動関数のものと共有します。ax_en は右下のパネルで系のハミルトニアンのログをプロットします。これら下２つのグラフは縦軸を時間 t とし共有しています。

1フレーム目のグラフを描写します。

ax_V.plot(xs, Vs, label="\$V(x)\$", color="black", alpha=0.5)
line_r, = ax_ϕ.plot(xs, real(ϕs), linewidth=1, linestyle="--", label="\$\\Re(\\phi)\$")
line_i, = ax_ϕ.plot(xs, imag(ϕs), linewidth=1, linestyle="--", label="\$\\Im(\\phi)\$")
line_a, = ax_ϕ.plot(xs, abs.(ϕs), linewidth=2, label="\$|\\phi|\$")
ax_ϕ.axhline(y = 0.0, xmin=minimum(xs), xmax=maximum(xs), linestyle=":", color="black", linewidth=1)
line_center, = ax_ϕ.plot([wp_init.r, wp_init.r], [ymin, ymax], label="WP center")
# rect = PyPlot.fill_betweenx([ymin, ymax], (wp_init.x - wp_init.G/2).*[1, 1], (wp_init.x + wp_init.G/2).*[1, 1], alpha=0.3)
rect = ax_ϕ.fill([xmin, xmax, xmin], [ymin, ymin, ymax], [xmax, xmax, xmin], [ymin, ymax, ymax], alpha=0.3, color="red", linewidth=0)
line_traj, = ax_traj.plot(traj_r, traj_T, label="WP center\n Trajectory")
line_en, = ax_en.plot(traj_H, traj_T, label="Hamiltonian")

ax_ϕ.legend()
ax_traj.legend(loc="lower left")
ax_en.legend(loc="lower left")
ax_V.legend()

波動関数のプロットにおいて、中心位置に縦線を書き、また波束の幅に対応する領域を薄く赤い四角でfillします。この領域を塗りつぶすのに、普通は fill_between(x) を使うと思いますが、これだと時間発展のときにデータを更新する（塗りつぶす領域の頂点座標を書き換える）方法がよくわからなかったので、 fill を使って3角形のポリゴン2つを自分で描くようにしました。そのせいで赤い領域に斜線が入ってしまっています。

PyPlotの準備ができましたので、時間発展ループに以下を追加します。forループ内にあるので、インデントを下げております。2ステップごとに更新することにしました。なお、高々４つの変数のMDに対してこのグラフ描写は非常に重い計算ですので、速度を求めるなら軌跡を適当なファイルに書き込むかメモリに蓄え、計算が終わってからグラフを書くべきかと思います。

以降、MDが進むと line_* オブジェクト中のデータを書き換えることで線グラフの更新をし、ポリゴンのリスト rect を更新することで波動関数の幅を示す赤色領域を動かします。

    if i % 2 == 0
        ϕs = [ϕ(x, wp) for x in xs]
        line_r.set_data(xs, real(ϕs))
        line_i.set_data(xs, imag(ϕs))
        line_a.set_data(xs, abs.(ϕs))
        line_center.set_data([wp.r, wp.r], [ymin, ymax])
        xmin = wp.r - wp.G
        xmax = wp.r + wp.G
        rect[1].set_xy([[xmin, ymin], [xmax, ymin], [xmin, ymax]])
        rect[2].set_xy([[xmax, ymin], [xmax, ymax], [xmin, ymax]])

        T = i*dt
        append!(traj_T, T)
        append!(traj_H, Hamiltonian(wp) - H0)
        append!(traj_r, wp.r)
        line_en.set_data(traj_H, traj_T)
        ax_en.set_ylim([0, T])
        ax_en.set_xlim([minimum(traj_H), maximum(traj_H)])

        line_traj.set_data(traj_r, traj_T)
        ax_traj.set_ylim([0, T])
        PyPlot.pause(0.0001)
        PyPlot.savefig("F:/work/semiclassical_wp/frames/T$i.png")
    end

計算チェック

計算誤差

2次の精度（Verlet法と同じ）ですので、時間幅 dt を $n$ 倍にすると保存量の数値誤差の幅は $n^3$ 倍程度になります。

トンネル効果が起こらないような速度を与えて井戸の底での運動で確かめます。

初期条件としてはこんな感じで、$(r, G, p, K) = (0.82, 0.32, 0.5, 0)$とします。

wp_init = wavepacket(0.82, 0.32, 0.5, 0.0)

$dt = 0.01$ のときにある程度動かしたときの様子です。

$\mathrm{std}[H] = 3.02\times 10^{-7}$ くらいの幅ですね。

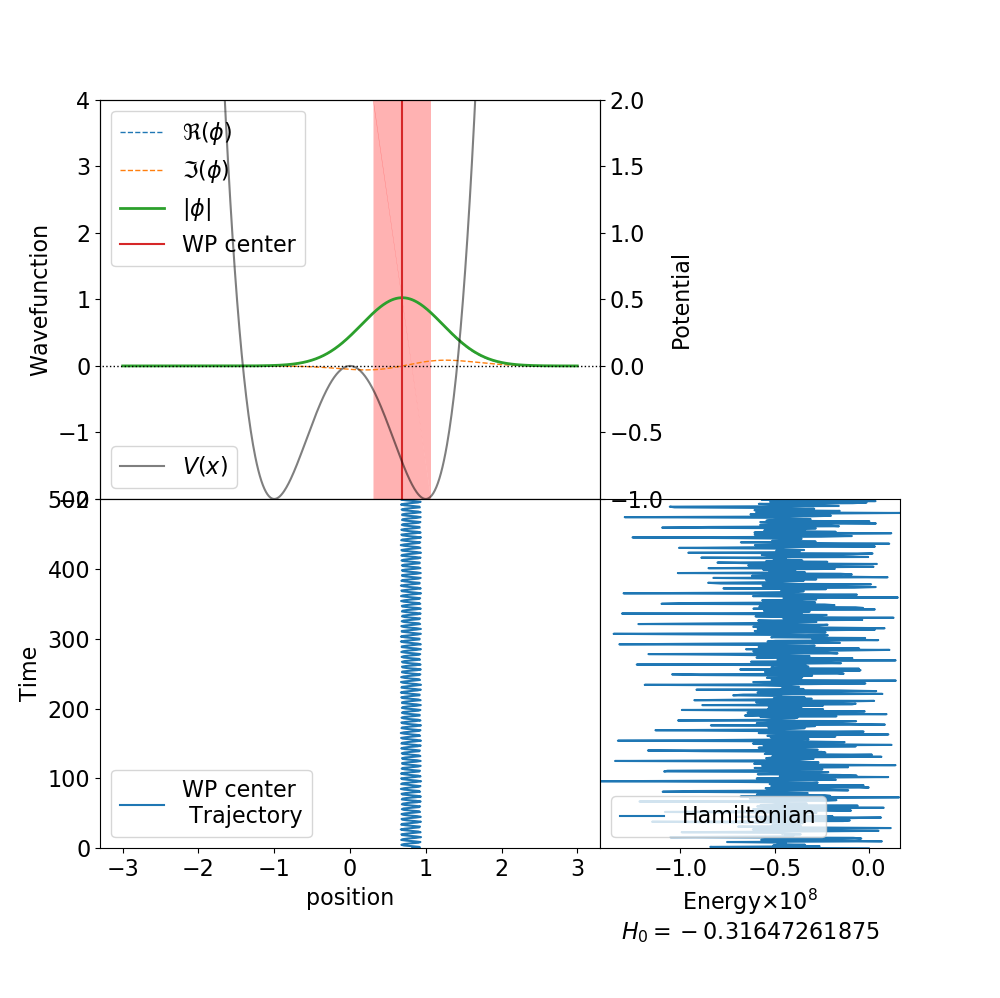
続いて$dt = 0.001$ と10分の1にしたとき

今度は$\mathrm{std}[H] = 3.00\times 10^{-9}$ くらいの幅になりました。

あれ、1000分の1くらいになってほしいのに100分の1程度・・・まあいっか

物理現象

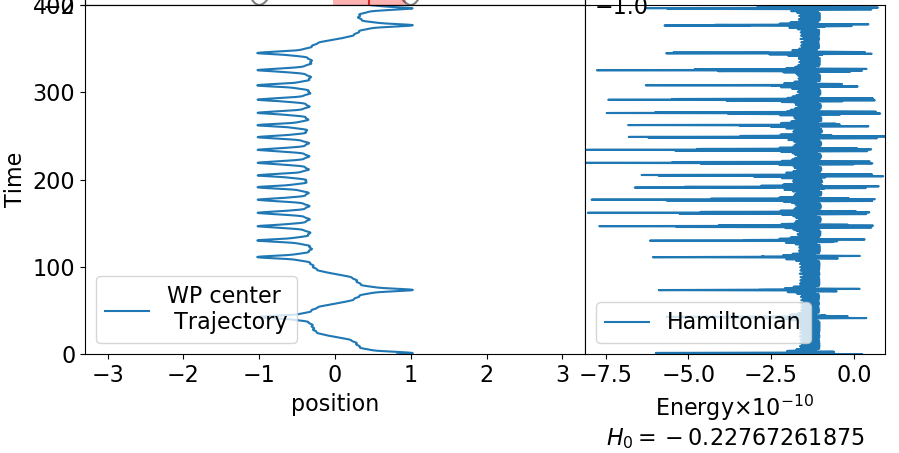
最初のアニメーションのように、総エネルギーが0に近いと障壁を超えるトンネル現象がみられます。

初期条件としてはこんな感じで、$(r, G, p, K) = (0.82, 0.32, 0.98, 0)$とします。

wp_init = wavepacket(0.82, 0.32, 0.98, 0.0)

dt = 0.0001 のとき

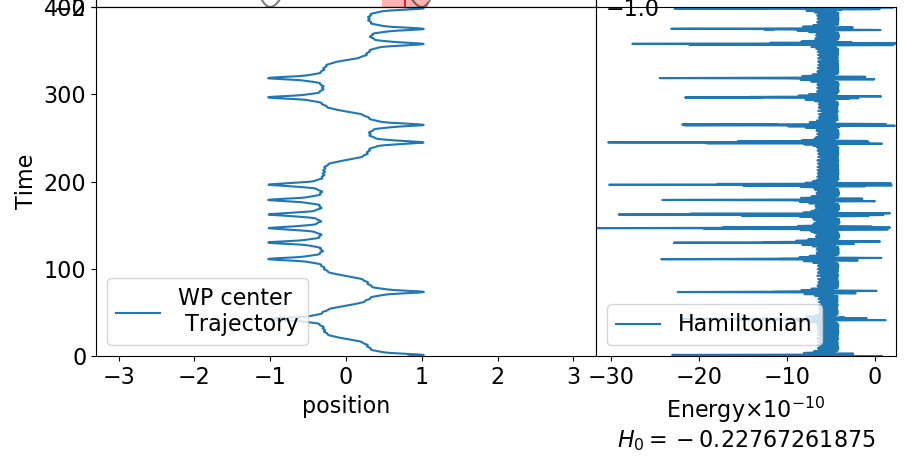
dt = 0.0002 のとき

途中からなんか軌跡が変わっていますね。トンネルするタイミングが違います。

$\Delta t$ は数値積分の時の都合で、物理には関係ないはずです。
もし変わるとしたら、現象を左右するレベルで数値積分誤差があるということです。

最初の10回弱の壁の衝突でトンネルする・しないは一致しているのですが、だんだんとずれてきています。 $\Delta t = 0.0001$は相当小さい設定ですが、それでもすぐにずれてくるので、この手法でのトンネル現象は相当センシティブな現象のようです。

座標のトラジェクトリを拡大すると、井戸の中を往復する周期に比べて細かく振動しています。これは波束の幅の振動に対応します。

この波束中心の振動と、波束幅の振動が別のタイミングで動いていて、これらが偶然いい感じの位相の組み合わせになったときにトンネルするようです。
このいい感じの組み合わせというのがすごい繊細で、微妙な誤差で結果が変わるんじゃないかと思っています。

とってつけたような議論

全エネルギーが時間発展してもドリフトしていないので、大きな間違いはしていなさそうです。
初期位置は $r = 0.25$ で、全エネルギーも負になっていました。これは古典粒子であれば $x=0$ の壁を超えることはできません。しかし、 $x < 0$ の領域にも踏み込むことがあります。これはトンネル効果を再現できているものと思います。
壁の中、 $x = 0$ 付近にいるときも全エネルギーは増えていません。これは今回の手法ではトンネル効果の発動中は波束の幅を広げて全エネルギーの期待値を下げることで全エネルギーを保存できていると考えられます。

ちなみに、この波束の絶対値もやはり粒子を観測する確率になります。もし $x = 0$ などポテンシャルが初期の全エネルギーより大きいところで観測して波束が収縮したとき、エネルギー保存則はどうなるかという話ですが、まあ観測するということは観測装置など系外と相互作用しているので、そこからエネルギーが与えられています。

余談１

途中の式は計算がめんどいのでこちらの論文のものをほぼそのまま使いました。今回はこの論文の熱浴がない系になります。あと記号を変えました。
https://www.sciencedirect.com/science/article/abs/pii/S0009261403010248

ちなみに $V(x)$ がガウス積分と相性が悪く解析的に計算できないとき、展開するという方法があります。

https://aip.scitation.org/doi/abs/10.1063/1.4762840
https://www.sciencedirect.com/science/article/abs/pii/S000926141301436X

余談２

この方法は東京女子大学の安藤先生が分子科学の夏の学校か何かで話していたのを聞いて知ったものです。いろいろ調べると波束を古典的に扱う方法が昔からあるようで、それらがどこまで似ているのかは、半古典法の勉強がてらいずれ調べてみようと思います。

余談３

こういうシミュレーションの書き方のベストプラクティスってなんだろう。immutableな構造体で定義して更新のたびに構造体を作り直す感じ（多分、関数型でよく見る流れ）で書きましたが、構造体のメンバ変数を必要に応じて書き換えるほうがいいのかもしれないし、むしろ構造体を使わないほうがいいのかもしれない。系で変更する必要のある変数の数や種類によってもやり方は変わってくる気がします。