前回の記事 で中心がずれているガウス積分×$x^n$ の積分の解析解を求めました。今回はそれを数値計算で確かめます。
環境
- Windows 10 (2021/2/13での最新)
- Julia 1.5.1
依存パッケージ
- QuadGK
- 数値積分に使います。
- SpecialFunctions
- 虚数誤差関数があります。
- PyPlot
- 結果の可視化です。
コードスニペット群
0または正の次数
$$
I_n(r,a) = \int_{-\infty}^\infty x^n\exp\left(-a(x - r)^2\right)dx
$$
について、$n\ge 0$ のケースです。
数値計算
using QuadGK
function numerical_plus(a, r, n)
f(x) = exp( - a*(x - r)^2)*(x^n)
ret = quadgk(f, -Inf, Inf)
return ret[1]
end
quadgk の戻り値は (result, error) のタプルです。今回は誤差は気にしないので、1番目の成分だけ取ります。
解析解
前回の記事から、漸化式と初期値
$$
I_{n+1}(r, a) = rI_n(r, a) + \frac{1}{2a}\frac{\partial I_n(r, a)}{\partial r}
$$
$$
I_0(r, a) = \sqrt{\pi/a}
$$
をコードに落とし込みます。
function Iplus(a, r, n)
p = [0.0 for i in 0:n]
p[1] = 1.0
ns = [i for i in 0:n]
for i in 1:n
pn1 = p[1:i].*1.0
pn2 = p[1:i+1].*ns[1:i+1] ./ (2*a)
p[i+1] = 0.0
p[1:i] .= pn2[2:i+1]
p[2:i+1] .+= pn1
end
return sum(p.*(r.^ns))*sqrt(pi/a)
end
p[i] は $r$ の $i - 1$ 次の係数です。例えば、 p = [1.0, 2.0, 0.0, 0.5] のときは $1.0 + 2.0r + 0.5r^3$ に対応します。
ns[i] は次数 $i-1$ を持ち、微分時の係数や最後合計時の累乗数に使います。
p = [0.0 for i in 0:n]とp[1] = 1.0の2行は $I_0$ での初期化に相当します。
forループは $I_0$ から順に $I_n$ で $\sqrt{\pi/a}$ に掛かる $r$ の多項式の係数を計算していってます。
ループ内ですが、
- 1行目
pn1 = p[1:i].*1.0・・・ $rI_n$ - 2行目
pn2 = p[1:i+1].*ns[1:i+1] ./ (2*a)・・・ $\frac{1}{2a}\frac{\partial I_n}{\partial r}$ - 後半3行 ・・・ $I_{n+1} = (I_{n} の何か)$ の更新
に対応します。
ループ番号iの時は高々 $i$ 次までの係数しか見ていないので、forループ内では p のインデックスは i + 1 まで操作するようにしました。
最後の sum(p.*(r.^ns)) で $\sum_{i=0}^n p_i r^i$ を計算しています。
追記
漸化式を解くと
$$
I_n(r, a) = n!\sqrt{\frac{\pi}{a}}r^n\sum_{k=0}^{\lfloor n/2 \rfloor} \frac{1}{(n-2k)!k!}\left(\frac{1}{4ar^2}\right)^k
$$
となります。これをコードにすると
function Iplus_2(a, r, n)
nh = floor(n/2)
ar2 = 4*a*r^2
s = sum([1/(factorial(n - 2k)*factorial(k))/(ar2^k) for k in 0:nh])
return factorial(n)*r^n*s*sqrt(pi/a)
end
となりますが、factorial もありますし、なんだか計算量として実はあまり変わらないのでは、という気がしてきます。
一応結果は正しく得られました。
実行
中心位置$r$を $-10$から$10$まで$0.1$ 刻み、また$a$ を $0.5, 1.0, 1.5, 2.0$ で計算してみます。
using PyPlot
PyPlot.pygui(true)
as = [0.5*i for i in 1:4]
rs = [0.1*i - 10.1 for i in 1:201]
function test_plus(n)
for ai in as
num = numerical_plus.(ai, rs, n)
anl = Iplus.(ai, rs, n)
PyPlot.plot(rs, num, label="Numerical, \$a=$ai\$")
PyPlot.plot(rs, anl, linestyle=":", label="Analytical, \$a=$ai\$")
end
PyPlot.legend()
PyPlot.show()
end
上にて定義した numerical_plus と Iplus に .を付けてブロードキャストしています。 rs が配列なので、戻り値もそれをmapした配列になります。
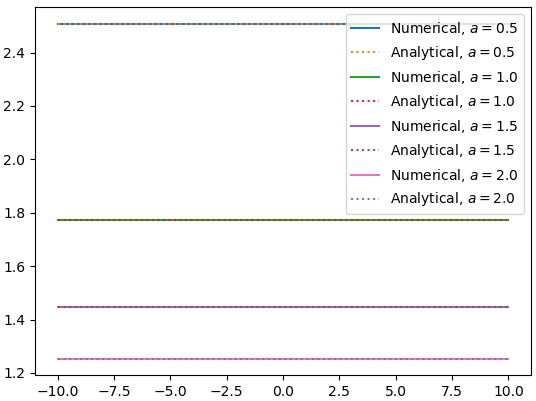
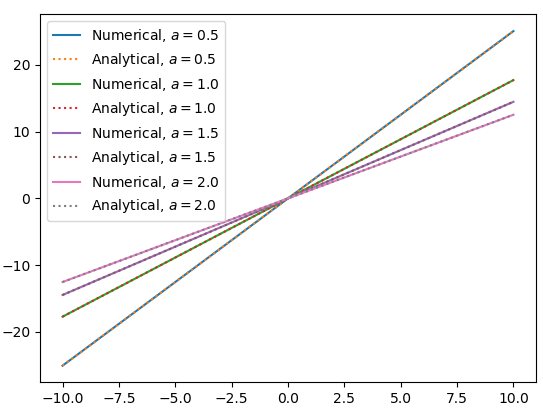
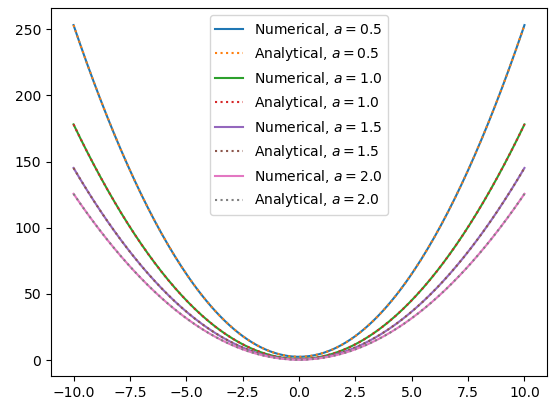
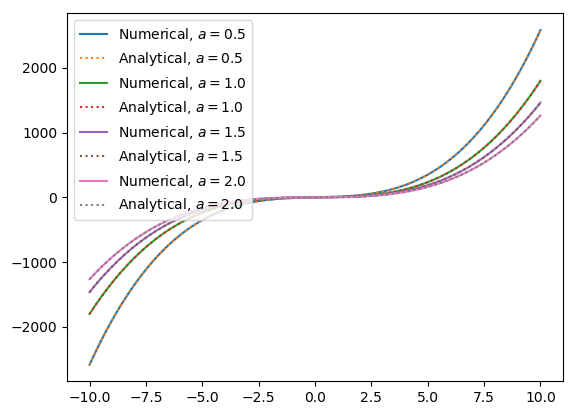
結果
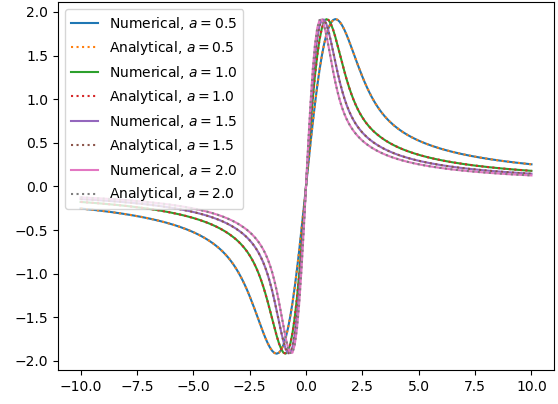
点線が解析解、実線が数値計算です。上に描く解析解を点線にしないと下にある数値計算の線が見えないほど一致しました。
- $n=0$
- $n=1$
- $n=2$
- $n=3$
-1次
$$
I_{-1}(r,a) = \int_{-\infty}^\infty \frac{1}{x}\exp\left(-a(x - r)^2\right)dx
$$
のケースです。
数値計算
using QuadGK
function numerical_minus(a, r, n, ϵ=1e-16)
f(x) = exp( - a*(x - r)^2)/(x^n)
m = quadgk(f, -Inf, -ϵ)
p = quadgk(f, ϵ, Inf)
return m[1] + p[1]
end
今回は $x=0$ で発散するので、これを積分区間から取り除かなくてはなりません。ということで、負の領域 $[-\infty, -\epsilon]$ での積分を m に、正の領域 $[\epsilon, \infty]$ での積分を p に持ち、最後に合計しています。まあコーシーの主値積分ですね。
これを確認するため、正負それぞれのみの積分結果、またその合計を確認してみます。
$a = 1.0$, $r = 1.0$ とします。確認用コードは以下のものです。
function test_converge(a, r, n)
ϵs = [1e-4, 1e-8, 1e-12, 1e-16, 1e-20]
for ϵ in ϵs
f(x) = exp( - a*(x - r)^2)/(x^n)
m = quadgk(f, -Inf, -ϵ)
p = quadgk(f, ϵ, Inf)
res = m[1] + p[1]
println("結果出力の何か")
end
end
test_converge(1.0, 1.0, 1)
| $\epsilon$ | 負領域 | 正領域 | 全体 |
|---|---|---|---|
| $1\times 10^{-4}$ | -2.860150609458353 | 4.767445645923802 | 1.9072950364654488 |
| $1\times 10^{-8}$ | -6.248371911808551 | 8.155814085335138 | 1.9074421735265865 |
| $1\times 10^{-12}$ | -9.63666677349307 | 11.544108961733365 | 1.907442188240294 |
| $1\times 10^{-16}$ | -13.02496164253371 | 14.932403830775474 | 1.907442188241765 |
| $1\times 10^{-20}$ | -16.413256511575103 | 18.320698699816877 | 1.9074421882417738 |
つまりこの積分は$x=0$ の前後で発散しますが、その発散具合がちょうどつり合い、一定の値に収束しているとみなすことができるようです。
解析解
$$
I_{-1}(r, a) = \pi\exp\left(-ar^2\right)\mathrm{erfi}\left(\sqrt{a} r\right)
$$
をそのまま書きます。 虚数誤差関数は SpecialFunctions パッケージにあります。
using SpecialFunctions
function Iminus1(a, r)
return pi*exp(-a*r^2)*erfi(sqrt(a)*r)
end
実行
function test_minus1()
for ai in as
num = [numerical_minus(ai, ri, 1) for ri in rs]
anl = [Iminus1(ai, ri) for ri in rs]
PyPlot.plot(rs, num, label="Numerical, \$a=$ai\$")
PyPlot.plot(rs, anl, linestyle=":", label="Analytical, \$a=$ai\$")
end
PyPlot.legend()
PyPlot.show()
end
さきほどは .を付けてブロードキャストしましたが、今回はリスト内法表記でやってみました。
このコードを実行するとこんな感じのグラフが得られます。
今回も後に引く解析解を点線にしないと数値計算が見れないくらい一致していました。
式見ればそうなのですが、最大値が $a$ に依らないことが分かります。
-2次
$$
I_{-2}(r,a) = \int_{-\infty}^\infty \frac{1}{x^2}\exp\left(-a(x - r)^2\right)dx
$$
のときです。
正負の領域に分けて足したとき、積分値が $\epsilon$ によってどう動くかを見てみます。今回も$a = 1.0$, $r = 1.0$ とします。
| $\epsilon$ | 負領域 | 正領域 | 全体 |
|---|---|---|---|
| $1\times 10^{-4}$ | 3672.059656386843 | 3685.7990701407916 | 7357.858726527635 |
| $1\times 10^{-8}$ | 3.678793060583596e7 | 3.678795789842806e7 | 7.357588850426403e7 |
| $1\times 10^{-12}$ | 3.678794411511545e11 | 3.6787944119200024e11 | 7.357588823431548e11 |
| $1\times 10^{-16}$ | 3.678794411714398e15 | 3.6787944117144515e15 | 7.35758882342885e15 |
| $1\times 10^{-20}$ | 3.678794411714423e19 | 3.678794411714423e19 | 7.357588823428846e19 |
順調に発散している様子が見れます。 $r=1$、つまり中心がずれているので正負領域それぞれで値が違ってくるはずですがそれも埋もれていっています。
よく考えると被積分関数は常に正で、 $1/x$ の時のように正負打ち消しあうことが期待できません。ということで、すくなくとも奇数次でないと収束しなさそうです。
-3次
ということで、$-1$の次の奇数次のものを確認してみます。
$$
I_{-3}(r,a) = \int_{-\infty}^\infty \frac{1}{x^3}\exp\left(-a(x - r)^2\right)dx
$$
今回も$a = 1.0$, $r = 1.0$ とします。
| $\epsilon$ | 負領域 | 正領域 | 全体 |
|---|---|---|---|
| $1\times 10^{-4}$ | -1.838661852830539e7 | 1.8401332068535633e7 | 14713.540230244398 |
| $1\times 10^{-8}$ | -1.8393971322813302e15 | 1.839397279433106e15 | 1.4715177575e8 |
| $1\times 10^{-12}$ | -1.8393972058498538e23 | 1.8393972058645694e23 | 1.471563169792e12 |
| $1\times 10^{-16}$ | -1.839397205857211e31 | 1.8393972058572123e31 | 1.3510798882111488e16 |
| $1\times 10^{-20}$ | -1.8393972058572115e39 | 1.8393972058572115e39 | 0.0 |
全体の積分値がどんどん大きくなり、ついに倍精度では持ちきれなくなって $0$ になりました。少なくとも普通の収束はしなさそうです。
まとめ
ということで、前回の記事の計算結果は数値計算で確認できました。
実は数値計算コードも書きながら前回の記事の計算をしていて、多くの計算ミスを修正できました。
なんでこの話にこんな手間かけたんだろ。